Minimum amount of lamps needed to be installed
Last Updated :
09 Sep, 2022
Given string str containing only dots and asterisk. A dot represents free spaces and 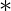 represents lamps. A lamp at position
represents lamps. A lamp at position 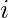 can spread its light at locations i-1, i, and i+1. Determine the minimum number of lamps needed to illuminate the whole string.
can spread its light at locations i-1, i, and i+1. Determine the minimum number of lamps needed to illuminate the whole string.
Examples:
Input: str = “……”
Output: 2
There are initially no lamps so the whole string is in dark.We will install lamps at position 2 and 5.The lamp at position 2 will illuminate 1, 2, 3 and lamp at position 5 will illuminate 4, 5, 6 thus the whole string is illuminated.
Input: str = “*.*”
Output: 0
Approach: If we don’t have an asterisk 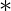 then for every 3 dots we need one lamp, so the answer is ceil(D/3) where D is the number of dots. The problem can be solved by creating a copy of the given string, and for each asterisk in the first string, we place an asterisk at its adjacent indices in the second string.
then for every 3 dots we need one lamp, so the answer is ceil(D/3) where D is the number of dots. The problem can be solved by creating a copy of the given string, and for each asterisk in the first string, we place an asterisk at its adjacent indices in the second string.
So if the given string is “…**..” then the second string will be “..****.”.
After that, we count the number of dots in each block of consecutive dots and find the number of needed lamps for that block, For each block, the answer will be ceil(D/3) and the total sum of these lamps will be the answer for the complete string.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void check(int n, string s)
{
char v[n];
for(int i = 0; i < n; i++)
{
if (s[i] == '*')
{
v[i] = '*';
if (i > 0 && i < n - 1)
{
v[i + 1] = '*';
v[i - 1] = '*';
}
if (i == 0 && n != 1)
{
v[i + 1] = '*';
}
if (i == n - 1 && n != 1)
{
v[i - 1] = '*';
}
}
else
{
if (v[i] != '*')
{
v[i] = '.';
}
}
}
string str(v);
string word = "";
char dl = '*';
int num = 0;
str = str + dl;
int l = str.size();
vector<string> res;
for (int i = 0; i < l; i++) {
if (str[i] != dl)
word += str[i];
else {
if ((int)word.size() != 0)
res.push_back(word);
word = "";
}
}
int ans = 0;
for(auto x : res)
{
if (x.length() == 0)
{
continue;
}
ans += ceil(x.length() * 1.0 / 3);
}
cout << ans << "\n";
}
int main() {
string s = ".....";
int n = s.length();
check(n, s);
return 0;
}
|
Java
import java.io.*;
import java.lang.*;
import java.util.*;
class GFG{
static void check(int n, String s)
{
char v[] = new char[n];
for(int i = 0; i < n; i++)
{
if (s.charAt(i) == '*')
{
v[i] = '*';
if (i > 0 && i < n - 1)
{
v[i + 1] = '*';
v[i - 1] = '*';
}
if (i == 0 && n != 1)
{
v[i + 1] = '*';
}
if (i == n - 1 && n != 1)
{
v[i - 1] = '*';
}
}
else
{
if (v[i] != '*')
{
v[i] = '.';
}
}
}
String xx = new String(v);
String x[] = xx.split("\\*");
int ans = 0;
for(String xi : x)
{
if (xi.length() == 0)
{
continue;
}
ans += Math.ceil(xi.length() * 1.0 / 3);
}
System.out.println(ans);
}
public static void main(String[] args)
{
String s = "......";
int n = s.length();
check(n, s);
}
}
|
Python3
import math
def check(n, s):
v = [""] * n
for i in range(n):
if (s[i] == "*"):
v[i] = "*"
if (i > 0 and i < n - 1):
v[i + 1] = "*"
v[i - 1] = "*"
if (i == 0 and n != 1):
v[i + 1] = "*"
if (i == n - 1 and n != 1):
v[i - 1] = "*"
else:
if (v[i] != "*"):
v[i] = "."
xx = ''.join(v)
x = xx.split("*")
s = 0
for i in range(len(x)):
if (x[i] == ""):
continue
s += math.ceil(len(x[i]) / 3)
print(s)
s = "......"
n = len(s)
check(n, s)
|
C#
using System;
class GFG {
static void check(int n, string s)
{
char[] v = new char[n];
for (int i = 0; i < n; i++) {
if (s[i] == '*') {
v[i] = '*';
if (i > 0 && i < n - 1) {
v[i + 1] = '*';
v[i - 1] = '*';
}
if (i == 0 && n != 1) {
v[i + 1] = '*';
}
if (i == n - 1 && n != 1) {
v[i - 1] = '*';
}
}
else {
if (v[i] != '*') {
v[i] = '.';
}
}
}
string xx = new string(v);
string[] x = xx.Split("\\*");
int ans = 0;
foreach(string xi in x)
{
if (xi.Length == 0) {
continue;
}
ans += (int)(Math.Ceiling(xi.Length * 1.0 / 3));
}
Console.Write(ans);
}
public static void Main(string[] args)
{
string s = "......";
int n = s.Length;
check(n, s);
}
}
|
Javascript
<script>
const check = (n, s) => {
let v = new Array(n).fill('');
for (let i = 0; i < n; i++)
{
if (s[i] == '*')
{
v[i] = '*';
if (i > 0 && i < n - 1) {
v[i + 1] = '*';
v[i - 1] = '*';
}
if (i == 0 && n != 1) {
v[i + 1] = '*';
}
if (i == n - 1 && n != 1) {
v[i - 1] = '*';
}
}
else {
if (v[i] != '*') {
v[i] = '.';
}
}
}
let str = v.join('');
let word = "";
let dl = '*';
let num = 0;
str = str + dl;
let l = str.length;
let res = [];
for (let i = 0; i < l; i++) {
if (str[i] != dl)
word = word + str[i];
else {
if (word.length != 0)
res.push(word);
word = "";
}
}
let ans = 0;
for (let x in res) {
if (res[x].length == 0) {
continue;
}
ans += Math.ceil(res[x].length * 1.0 / 3);
}
document.write(`${ans}<br/>`);
}
let s = ".....";
let n = s.length;
check(n, s);
</script>
|
Complexity Analysis:
- Time Complexity: O(n) as we are doing single loop traversal
- Space Complexity: O(n) as we are creating a character array
Note: where n is the size of the string given
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...