Minimize the difference between the maximum and minimum values of the modified array
Last Updated :
07 Sep, 2022
Given an array A of n integers and integer X. You may choose any integer between 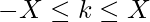 , and add k to A[i] for each
, and add k to A[i] for each 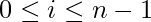 . The task is to find the smallest possible difference between the maximum value of A and the minimum value of A after updating array A.
. The task is to find the smallest possible difference between the maximum value of A and the minimum value of A after updating array A.
Examples:
Input: arr[] = {1, 3, 6}, x = 3
Output: 0
New array is [3, 3, 3] or [4, 4, 4].
Input: arr[] = {0, 10}, x = 2
Output: 6
New array is [2, 8] i.e add 2 to a[0] and subtract -2 from a[1].
Approach: Let A be the original array. Towards trying to minimize max(A) – min(A), let’s try to minimize max(A) and maximize min(A) separately.
The smallest possible value of max(A) is max(A) – K, as the value max(A) cannot go lower. Similarly, the largest possible value of min(A) is min(A) + K. So the quantity max(A) – min(A) is at least ans = (max(A) – K) – (min(A) + K).
We can attain this value, by the following modifications
- If A[i] <= min(A) + K, then A[i] = min(A) + K
- Else, if A[i] >= max(A) – K, then A[i] = max(A) – K
If ans < 0, the best answer we could have is ans = 0, also using the same modification.
Below is the implementation of above approach.
C++
#include <bits/stdc++.h>
using namespace std;
int minDiff(int n, int x, int A[])
{
int mn = A[0], mx = A[0];
for (int i = 0; i < n; ++i) {
mn = min(mn, A[i]);
mx = max(mx, A[i]);
}
return max(0, mx - mn - 2 * x);
}
int main()
{
int n = 3, x = 3;
int A[] = { 1, 3, 6 };
cout << minDiff(n, x, A);
return 0;
}
|
Java
import java.util.*;
class GFG
{
static int minDiff(int n, int x, int A[])
{
int mn = A[0], mx = A[0];
for (int i = 0; i < n; ++i) {
mn = Math.min(mn, A[i]);
mx = Math.max(mx, A[i]);
}
return Math.max(0, mx - mn - 2 * x);
}
public static void main(String []args)
{
int n = 3, x = 3;
int A[] = { 1, 3, 6 };
System.out.println(minDiff(n, x, A));
}
}
|
Python3
def minDiff( n, x, A):
mn = A[0]
mx = A[0]
for i in range(0,n):
mn = min( mn, A[ i])
mx = max( mx, A[ i])
return max(0, mx - mn - 2 * x)
n = 3
x = 3
A = [1, 3, 6 ]
print(minDiff( n, x, A))
|
C#
using System;
class GFG
{
static int minDiff(int n, int x, int []A)
{
int mn = A[0], mx = A[0];
for (int i = 0; i < n; ++i) {
mn = Math.Min(mn, A[i]);
mx = Math.Max(mx, A[i]);
}
return Math.Max(0, mx - mn - 2 * x);
}
public static void Main()
{
int n = 3, x = 3;
int []A = { 1, 3, 6 };
Console.WriteLine(minDiff(n, x, A));
}
}
|
PHP
<?php
function minDiff($n, $x, $A)
{
$mn = $A[0];
$mx = $A[0];
for ($i = 0; $i < $n; ++$i) {
$mn = min($mn, $A[$i]);
$mx = max($mx, $A[$i]);
}
return max(0, $mx - $mn - 2 * $x);
}
$n = 3;
$x = 3;
$A = array( 1, 3, 6 );
echo minDiff($n, $x, $A);
?>
|
Javascript
<script>
function minDiff( n, x, A)
{
var mn = A[0], mx = A[0];
for (var i = 0; i < n; ++i) {
mn = Math.min(mn, A[i]);
mx = Math.max(mx, A[i]);
}
return Math.max(0, mx - mn - 2 * x);
}
var n = 3, x = 3;
var A = [ 1, 3, 6 ];
document.write( minDiff(n, x, A));
</script>
|
Complexity Analysis:
- Time Complexity: O(n)
- Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...