Minimize difference between two sequences obtained by splitting first N powers of 2
Last Updated :
07 Apr, 2021
Given a positive even number N, the task is to split the first N powers of 2 into two equal sequences such that the absolute difference between their sum is minimized. Print the minimum difference obtained.
Examples:
Input: N = 2
Output: 2
Explanation:
The sequence is {2, 4}.
Only possible way to split the sequence is {2}, {4}. Therefore, difference = 4 ? 2 = 2.
Input: N = 4
Output: 6
Explanation:
The sequence is {2, 4, 8, 16}.
The most optimal way is to split the sequence as {2, 16}, {4, 8}. The difference is (2 + 16) ? (4 + 8) = 6.
Naive Approach: The simplest approach to solve this problem is to generate all possible combinations of N/2 elements of the sequence and store their sum. Then, find the minimum difference among all the sum of the pairs.
Time Complexity: O(2N)
Auxiliary Space: O(N)
Approach: The above approach can also be optimized as per the following observations:
- As 2N is greater than the sum of all the other elements combined:
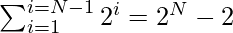
- The subarray having the largest element will always have a larger sum. Therefore, to minimize the differences between their sum, the idea is to put the (N/2 – 1) smallest elements into the subarray with the largest element.
Follow the steps below to solve the problem:
- Initialize two variables, sum1 = 0 and sum2 = 0, to store the sum of the first subarray and the second subarray respectively.
- Add the sum of
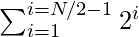 and 2N to the variable sum1.
and 2N to the variable sum1. - Add the sum of
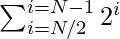 to the variable sum2.
to the variable sum2. - After completing the above steps, print the difference between sum1 and sum2.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void minimumDifference(int N)
{
int sum1 = (1 << N), sum2 = 0;
for (int i = 1; i < N / 2; i++)
sum1 += (1 << i);
for (int i = N / 2; i < N; i++)
sum2 += (1 << i);
cout << sum1 - sum2;
}
int main()
{
int N = 4;
minimumDifference(N);
return 0;
}
|
Java
import java.util.*;
class GFG
{
static void minimumDifference(int N)
{
int sum1 = (1 << N), sum2 = 0;
for (int i = 1; i < N / 2; i++)
sum1 += (1 << i);
for (int i = N / 2; i < N; i++)
sum2 += (1 << i);
System.out.println(sum1 - sum2);
}
public static void main(String args[])
{
int N = 4;
minimumDifference(N);
}
}
|
Python3
def minimumDifference(N):
sum1 = (1 << N)
sum2 = 0
for i in range(1, N // 2):
sum1 += (1 << i)
for i in range( N // 2, N):
sum2 += (1 << i)
print(sum1 - sum2)
N = 4
minimumDifference(N)
|
C#
using System;
class GFG
{
static void minimumDifference(int N)
{
int sum1 = (1 << N), sum2 = 0;
for (int i = 1; i < N / 2; i++)
sum1 += (1 << i);
for (int i = N / 2; i < N; i++)
sum2 += (1 << i);
Console.WriteLine(sum1 - sum2);
}
static public void Main ()
{
int N = 4;
minimumDifference(N);
}
}
|
Javascript
<script>
function minimumDifference(N) {
var sum1 = (1 << N), sum2 = 0;
for (i = 1; i < N / 2; i++)
sum1 += (1 << i);
for (i = N / 2; i < N; i++)
sum2 += (1 << i);
document.write(sum1 - sum2);
}
var N = 4;
minimumDifference(N);
</script>
|
Time Complexity: O(N)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...