Minimize cost of painting N houses such that adjacent houses have different colors

Given an integer N and a 2D array cost[][3], where cost[i][0], cost[i][1], and cost[i][2] is the cost of painting i^th house with colors red, blue, and green respectively, the task is to find the minimum cost to paint all the houses such that no two adjacent houses have the same color.

Examples:

Input: N = 3, cost[][3] = {{14, 2, 11}, {11, 14, 5}, {14, 3, 10}}
Output: 10
Explanation:
Paint house 0 as blue. Cost = 2. Paint house 1 as green. Cost = 5. Paint house 2 as blue. Cost = 3.
Therefore, the total cost = 2 + 5 + 3 = 10.

Input: N = 2, cost[][3] = {{1, 2, 3}, {1, 4, 6}}
Output: 3

Naive Approach: The simplest approach to solve the given problem is to generate all possible ways of coloring all the houses with the colors red, blue, and green and find the minimum cost among all the possible combinations such that no two adjacent houses have the same colors. 
Time Complexity: (3^N)
Auxiliary Space: O(1)

Efficient Approach: The above approach can be optimized by using Dynamic Programming as there are overlapping subproblems that can be stored to minimize the number of recursive calls. The idea is to find the minimum cost of painting the current house by any color on the basis of the minimum cost of the other two colors of previously colored houses. Follow the steps below to solve the given problem:

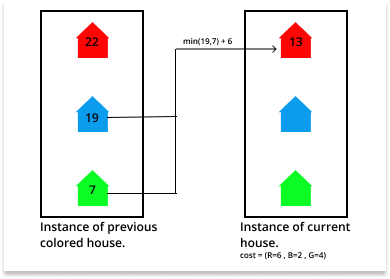
Follow the steps below to solve the problem:

• Create an auxiliary 2D dp[][3] array to store the minimum cost of previously colored houses.
• Initialize dp[0][0], dp[0][1], and dp[0][2] as the cost of cost[i][0], cost[i][1], and cost[i][2] respectively.
• Traverse the given array cost[][3] over the range [1, N] and update the cost of painting the current house with colors red, blue, and green with the minimum of the cost other two colors in dp[i][0], dp[i][1], and dp[i][2] respectively.
• After completing the above steps, print the minimum of dp[N – 1][0], dp[N – 1][1], and dp[N – 1][2] as the minimum cost of painting all the houses with different adjacent colors.

Below is the implementation of the above approach:

C++

// C++ program for the above approach

#include <bits/stdc++.h>
using namespace std;

// Function to find the minimum cost of
// coloring the houses such that no two
// adjacent houses has the same color
int minCost(vector<vector<int> >& costs,
            int N)
{
    // Corner Case
    if (N == 0)
        return 0;

    // Auxiliary 2D dp array
    vector<vector<int> > dp(
        N, vector<int>(3, 0));

    // Base Case
    dp[0][0] = costs[0][0];
    dp[0][1] = costs[0][1];
    dp[0][2] = costs[0][2];

    for (int i = 1; i < N; i++) {

        // If current house is colored
        // with red the take min cost of
        // previous houses colored with
        // (blue and green)
        dp[i][0] = min(dp[i - 1][1],
                       dp[i - 1][2])
                   + costs[i][0];

        // If current house is colored
        // with blue the take min cost of
        // previous houses colored with
        // (red and green)
        dp[i][1] = min(dp[i - 1][0],
                       dp[i - 1][2])
                   + costs[i][1];

        // If current house is colored
        // with green the take min cost of
        // previous houses colored with
        // (red and blue)
        dp[i][2] = min(dp[i - 1][0],
                       dp[i - 1][1])
                   + costs[i][2];
    }

    // Print the min cost of the
    // last painted house
    cout << min(dp[N - 1][0],
                min(dp[N - 1][1],
                    dp[N - 1][2]));
}

// Driver Code
int main()
{
    vector<vector<int> > costs{ { 14, 2, 11 },
                                { 11, 14, 5 },
                                { 14, 3, 10 } };
    int N = costs.size();

    // Function Call
    minCost(costs, N);

    return 0;
}

Java

// Java program for the above approach
import java.io.*;
import java.lang.*;
import java.util.*;

class GFG {

  // Function to find the minimum cost of
  // coloring the houses such that no two
  // adjacent houses has the same color
  static void minCost(int costs[][], int N)
  {

    // Corner Case
    if (N == 0)
      return;

    // Auxiliary 2D dp array
    int dp[][] = new int[N][3];

    // Base Case
    dp[0][0] = costs[0][0];
    dp[0][1] = costs[0][1];
    dp[0][2] = costs[0][2];

    for (int i = 1; i < N; i++) {

      // If current house is colored
      // with red the take min cost of
      // previous houses colored with
      // (blue and green)
      dp[i][0] = Math.min(dp[i - 1][1], dp[i - 1][2])
        + costs[i][0];

      // If current house is colored
      // with blue the take min cost of
      // previous houses colored with
      // (red and green)
      dp[i][1] = Math.min(dp[i - 1][0], dp[i - 1][2])
        + costs[i][1];

      // If current house is colored
      // with green the take min cost of
      // previous houses colored with
      // (red and blue)
      dp[i][2] = Math.min(dp[i - 1][0], dp[i - 1][1])
        + costs[i][2];
    }

    // Print the min cost of the
    // last painted house
    System.out.println(
      Math.min(dp[N - 1][0],
               Math.min(dp[N - 1][1], dp[N - 1][2])));
  }

  // Driver code
  public static void main(String[] args)
  {

    int costs[][] = { { 14, 2, 11 },
                     { 11, 14, 5 },
                     { 14, 3, 10 } };

    int N = costs.length;

    // Function Call
    minCost(costs, N);
  }
}

// This code is contributed by Kingash.

Python3

# Python 3 program for the above approach

# Function to find the minimum cost of
# coloring the houses such that no two
# adjacent houses has the same color
def minCost(costs, N):

    # Corner Case
    if (N == 0):
        return 0

    # Auxiliary 2D dp array
    dp = [[0 for i in range(3)] for j in range(3)]

    # Base Case
    dp[0][0] = costs[0][0]
    dp[0][1] = costs[0][1]
    dp[0][2] = costs[0][2]

    for i in range(1, N, 1):

        # If current house is colored
        # with red the take min cost of
        # previous houses colored with
        # (blue and green)
        dp[i][0] = min(dp[i - 1][1], dp[i - 1][2]) + costs[i][0]

        # If current house is colored
        # with blue the take min cost of
        # previous houses colored with
        # (red and green)
        dp[i][1] = min(dp[i - 1][0], dp[i - 1][2]) + costs[i][1]

        # If current house is colored
        # with green the take min cost of
        # previous houses colored with
        # (red and blue)
        dp[i][2] = min(dp[i - 1][0], dp[i - 1][1]) + costs[i][2]

    # Print the min cost of the
    # last painted house
    print(min(dp[N - 1][0], min(dp[N - 1][1],dp[N - 1][2])))

# Driver Code
if __name__ == '__main__':
    costs = [[14, 2, 11],
             [11, 14, 5],
             [14, 3, 10]]
    N = len(costs)

    # Function Call
    minCost(costs, N)

    # This code is contributed by ipg2016107.

C#

// C# program for the above approach
using System;
using System.Collections.Generic;
class GFG{

  // Function to find the minimum cost of
  // coloring the houses such that no two
  // adjacent houses has the same color
  static int minCost(List<List<int>>costs,
                     int N)
  {
    // Corner Case
    if (N == 0)
      return 0;

    // Auxiliary 2D dp array
    List<int> temp = new List<int>();
    for(int i=0;i<3;i++)
      temp.Add(0);
    List<List<int>> dp = new List<List<int>>();
    for(int i=0;i<N;i++)
      dp.Add(temp);

    // Base Case
    dp[0][0] = costs[0][0];
    dp[0][1] = costs[0][1];
    dp[0][2] = costs[0][2];

    for (int i = 1; i < N; i++) {

      // If current house is colored
      // with red the take min cost of
      // previous houses colored with
      // (blue and green)
      dp[i][0] = Math.Min(dp[i - 1][1],
                          dp[i - 1][2])
        + costs[i][0];

      // If current house is colored
      // with blue the take min cost of
      // previous houses colored with
      // (red and green)
      dp[i][1] = Math.Min(dp[i - 1][0],
                          dp[i - 1][2])
        + costs[i][1];

      // If current house is colored
      // with green the take min cost of
      // previous houses colored with
      // (red and blue)
      dp[i][2] = Math.Min(dp[i - 1][0],
                          dp[i - 1][1])
        + costs[i][2];
    }

    // Print the min cost of the
    // last painted house
    return (Math.Min(dp[N - 1][0], Math.Min(dp[N - 1][1],dp[N - 1][2])))-11;
  }

  // Driver Code
  public static void Main()
  {
    List<List<int>>costs = new List<List<int>>();
    costs.Add(new List<int>(){14, 2, 11});
    costs.Add(new List<int>(){11, 14, 5 });
    costs.Add(new List<int>(){14, 3, 10 });
    int N = 3;

    // Function Call
    Console.WriteLine((int)(minCost(costs, N)));
  }
}

// This code is contributed by bgangwar59.

Javascript

<script>
    // Javascript program for the above approach

    // Function to find the minimum cost of
    // coloring the houses such that no two
    // adjacent houses has the same color
    function minCost(costs, N)
    {
        // Corner Case
        if (N == 0)
            return 0;

        // Auxiliary 2D dp array
        let dp = new Array(N);
        for(let i = 0; i < N; i++)
        {
            dp[i] = new Array(3);
            for(let j = 0; j < 3; j++)
            {
                dp[i][j] = 0;
            }
        }

        // Base Case
        dp[0][0] = costs[0][0];
        dp[0][1] = costs[0][1];
        dp[0][2] = costs[0][2];

        for(let i = 1; i < N; i++)
        {
            // If current house is colored
            // with red the take min cost of
            // previous houses colored with
            // (blue and green)
            dp[i][0] = Math.min(dp[i - 1][1], dp[i - 1][2]) + costs[i][0];

            // If current house is colored
            // with blue the take min cost of
            // previous houses colored with
            // (red and green)
            dp[i][1] = Math.min(dp[i - 1][0], dp[i - 1][2]) + costs[i][1];

            // If current house is colored
            // with green the take min cost of
            // previous houses colored with
            // (red and blue)
            dp[i][2] = Math.min(dp[i - 1][0], dp[i - 1][1]) + costs[i][2];
        }

        // Print the min cost of the
        // last painted house
        document.write(Math.min(dp[N - 1][0], Math.min(dp[N - 1][1],dp[N - 1][2])));
    }

    let costs = [[14, 2, 11],
             [11, 14, 5],
             [14, 3, 10]];
    let N = costs.length;

    // Function Call
    minCost(costs, N);

    // This code is contributed by decode2207.
</script>

Output:

10

Time Complexity: O(N)
Auxiliary Space: O(N)