Mid-Point Line Generation Algorithm
Last Updated :
13 Sep, 2023
Given coordinate of two points A(x1, y1) and B(x2, y2) such that x1 < x2 and y1 < y2. The task to find all the intermediate points required for drawing line AB on the computer screen of pixels. Note that every pixel has integer coordinates.
We have discussed below algorithms for this task.
- DDA algorithm for line drawing
- Introduction to Bresenhams’s algorithm for line drawing.
In this post, Mid-Point Line drawing algorithm is discussed which is a different way to represent Bresenham’s algorithm introduced in previous post.
As discussed in previous post, for any given/calculated previous pixel P(Xp,Yp), there are two candidates for the next pixel closest to the line, E(Xp+1, Yp) and NE(Xp+1, Yp+1) (E stands for East and NE stands for North-East).
In Mid-Point algorithm we do following.
- Find middle of two possible next points. Middle of E(Xp+1, Yp) and NE(Xp+1, Yp+1) is M(Xp+1, Yp+1/2).
- If M is above the line, then choose E as next point.
- If M is below the line, then choose NE as next point.

How to find if a point is above a line or below a line?
Below are some assumptions to keep algorithm simple.
- We draw line from left to right.
- x1 < x2 and y1< y2
- Slope of the line is between 0 and 1. We draw a line from lower left to upper right.
Cases other than above assumptions can be handled using reflection.
Let us consider a line y = mx + B.
We can re-write the equation as :
y = (dy/dx)x + B or
(dy)x + B(dx) - y(dx) = 0
Let F(x, y) = (dy)x - y(dx) + B(dx) -----(1)
Let we are given two end points of a line (under
above assumptions)
-> For all points (x,y) on the line,
the solution to F(x, y) is 0.
-> For all points (x,y) above the line,
F(x, y) result in a negative number.
-> And for all points (x,y) below the line,
F(x, y) result in a positive number.
This relationship is used to determine the relative
position of M
M = (Xp+1, Yp+1/2)
So our decision parameter d is,
d = F(M) = F(Xp+1, Yp+1/2)
How to efficiently find new value of d from its old value?
For simplicity, let as write F(x, y) as ax + by + c.
Where a = dy
b = -dx
c = B*dx
We got these values from above equation (1)
Case 1: If E is chosen then for next point :
dnew = F(Xp+2, Yp+1/2)
= a(Xp+2) + b(Yp+1/2) + c
dold = a(Xp+1) + b(Yp+1/2) + c
Difference (Or delta) of two distances:
DELd = dnew – dold
= a(Xp+2)- a(Xp+1)+ b(Yp+1/2)- b(Yp+1/2)+ c-c
= a(Xp) +2a – a(Xp) – a
= a.
Therefore, dnew = dold + dy. (as a = dy)
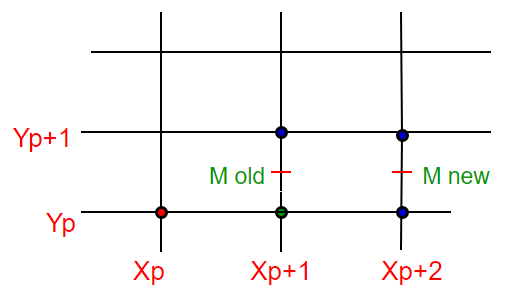
Case 2: If NE is chosen then for next point :
dnew = F(Xp+2, Yp+3/2)
= a(Xp+2) + b(Yp+3/2) + c
dold = a(Xp+1) + b(Yp+1/2) + c
Difference (Or delta) of two distances:
DELd = dnew -dold
= a(Xp+2)- a(Xp+1)+ b(Yp+3/2)- b(Yp+1/2)+ c-c
= a(Xp) + 2a – a(Xp) – a + b(Yp) + 3/2b – b(Yp) -1/2b
= a + b
Therefore, dnew = dold + dy – dx. (as a = dy , b = -dx)
Calculation For initial value of decision parameter d0:
d0 = F(X1+1 , Y1+1/2)
= a(X1 + 1) + b(Y1 + 1/2) +c
= aX1+ bY1 + c + a + b/2
= F(X1,Y1) + a + b/2
= a + b/2 (as F(X1, Y1) = 0 )
d0 = dy – dx/2. (as a = dy, b = -dx)
Algorithm:
Input (X1,Y1) and (X2,Y2)
dy = Y2- Y1
dx = X2 - X1
// initial value of
// decision parameter d
if(dy<=dx){
d = dy - (dx/2)
x = X1 , y = Y1
// plot initial given point
Plot(x , y)
// iterate through value of X
while(x < X2)
x = x+1
// 'E' is chosen
if (d < 0)
d = d + dy
// 'NE' is chosen
else
d = d + dy - dx
y = y+1
Plot(x,y)}
else if(dx<=dy)
{
d = dx - (dy/2)
x = X1 , y = Y1
// plot initial given point
Plot(x , y)
// iterate through value of X
while(y< Y2)
y= y+1
// 'E' is chosen
if (d < 0)
d = d + dx
// 'NE' is chosen
else
d = d + dx - dy
x= x+1
Plot(x,y)
}
Below is the implementation of above idea:
C++
#include<bits/stdc++.h>
using namespace std;
void midPoint(int X1, int Y1, int X2, int Y2)
{
int dx = X2 - X1;
int dy = Y2 - Y1;
if(dy<=dx){
int d = dy - (dx/2);
int x = X1, y = Y1;
cout << x << "," << y << "\n";
while (x < X2)
{
x++;
if (d < 0)
d = d + dy;
else
{
d += (dy - dx);
y++;
}
cout << x << "," << y << "\n";
}
}
else if(dx<dy)
{
int d = dx - (dy/2);
int x = X1, y = Y1;
cout << x << "," << y << "\n";
while (y < Y2)
{
y++;
if (d < 0)
d = d + dx;
else
{
d += (dx - dy);
x++;
}
cout << x << "," << y << "\n";
}
}
}
int main()
{
int X1 = 2, Y1 = 2, X2 = 8, Y2 = 5;
midPoint(X1, Y1, X2, Y2);
return 0;
}
|
Java
class GFG
{
static void midPoint(int X1, int Y1,
int X2, int Y2)
{
int dx = X2 - X1;
int dy = Y2 - Y1;
int d = dy - (dx/2);
int x = X1, y = Y1;
System.out.print(x +"," + y + "\n");
while (x < X2)
{
x++;
if (d < 0)
d = d + dy;
else
{
d += (dy - dx);
y++;
}
System.out.print(x +"," + y + "\n");
}
}
public static void main (String[] args)
{
int X1 = 2, Y1 = 2, X2 = 8, Y2 = 5;
midPoint(X1, Y1, X2, Y2);
}
}
|
Python 3
def midPoint(X1,Y1,X2,Y2):
dx = X2 - X1
dy = Y2 - Y1
d = dy - (dx/2)
x = X1
y = Y1
print(x,",",y,"\n")
while (x < X2):
x=x+1
if(d < 0):
d = d + dy
else:
d = d + (dy - dx)
y=y+1
print(x,",",y,"\n")
if __name__=='__main__':
X1 = 2
Y1 = 2
X2 = 8
Y2 = 5
midPoint(X1, Y1, X2, Y2)
|
C#
using System;
class GFG {
static void midPoint(int X1, int Y1,
int X2, int Y2)
{
int dx = X2 - X1;
int dy = Y2 - Y1;
int d = dy - (dx/2);
int x = X1, y = Y1;
Console.Write(x + "," + y + "\n");
while (x < X2)
{
x++;
if (d < 0)
d = d + dy;
else
{
d += (dy - dx);
y++;
}
Console.Write(x + "," + y + "\n");
}
}
public static void Main ()
{
int X1 = 2, Y1 = 2, X2 = 8, Y2 = 5;
midPoint(X1, Y1, X2, Y2);
}
}
|
PHP
<?php
function midPoint($X1, $Y1,
$X2, $Y2)
{
$dx = $X2 - $X1;
$dy = $Y2 - $Y1;
$d = $dy - ($dx/2);
$x = $X1;
$y = $Y1;
echo $x , "," , $y , "\n";
while ($x < $X2)
{
$x++;
if ($d < 0)
$d = $d + $dy;
else
{
$d += ($dy - $dx);
$y++;
}
echo $x , "," ,$y , "\n";
}
}
$X1 = 2;
$Y1 = 2;
$X2 = 8;
$Y2 = 5;
midPoint($X1, $Y1, $X2, $Y2);
?>
|
Javascript
<script>
function midPoint(X1, Y1, X2, Y2)
{
let dx = X2 - X1;
let dy = Y2 - Y1;
let d = dy - (dx/2);
let x = X1, y = Y1;
document.write(x +"," + y + "<br/>");
while (x < X2)
{
x++;
if (d < 0)
d = d + dy;
else
{
d += (dy - dx);
y++;
}
document.write(x + "," + y + "<br/>");
}
}
let X1 = 2, Y1 = 2, X2 = 8, Y2 = 5;
midPoint(X1, Y1, X2, Y2);
</script>
|
Output:
2,2
3,3
4,3
5,4
6,4
7,5
8,5
Time Complexity: O(x2 – x1)
Auxiliary Space: O(1)
References:
http://www.eng.utah.edu/~cs5600/slides/Wk%202%20Lec02_Bresenham.pdf
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...