Midpoint formula is ((x1 + x2)/2, (y1 + y2)/2). The coordinates of the two points are (x1, y1) and (x2, y2) respectively, and the midpoint is a point that lies halfway between these two points.
Mid Point is a foundational concept in coordinate geometry. It plays a crucial role in finding the midpoint of a line segment. There are instances in Coordinate Geometry where we need to know the mid-point of two given points or the mid-point of a line segment. In this case, we use Mid Point formula as it is a simple and effective way to calculate the midpoint of any given line segment, regardless of its length or position on the coordinate plane.
We have covered Mid Point Formula in detail, with its derivation using the similarity of triangles. Along with it, we have curated the solved examples on Mid Point Formula.
Mid Point Definition
The point which divides the line exactly in two equal halves is the midpoint of the line. In other words, the ratio of both halves of the line in which the midpoint divides it is 1:1.
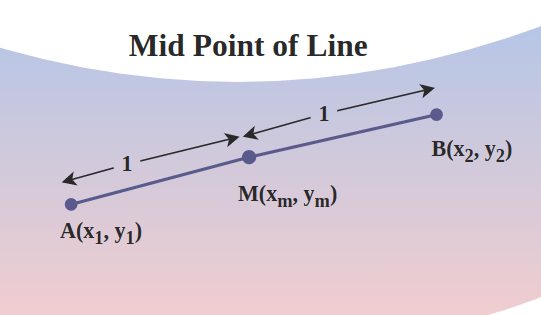
Mid Point of Line
For a line segment AB in Cartesian coordinate where the x-axis coordinate of point A is x1 and the y-axis coordinate of point A is y1 and similarly, the x-axis coordinate of point B is x2 and the y-axis coordinate of point B is y2, the mid-point of the line will be given by (xm, ym).
The formula for the mid-point (xm, ym) is:

Mid Point Formula
Let P(x1,y1) and Q(x2,y2) be the two ends of a given line in a coordinate plane, and R(x,y) be the point on that line which divides PQ in the ratio m1:m2 such that
PR/RQ = m1/m2 . . .(1)

Derivation of Mid Point Formula
Drawing lines PM, QN, and RL perpendicular on the x-axis and through R draw a straight line parallel to the x-axis to meet MP at S and NQ at T.
Hence from the figure, we can say:
SR = ML = OL – OM = x – x1 . . . (2)
RT = LN = ON – Ol = x2 – x . . . (3)
PS = MS – MP = LR – MP = y – y1 . . . (4)
TQ = NQ – NT = NQ – LR = y2 – y . . . (5)
Now triangle ∆SPR is similar to triangle ∆TQR.
Therefore,
SR/RT = PR/RQ
By using equations 2, 3, and 1, we know:
x – x1 / x2 – x = m1 / m2
⇒ m2x – m2x1 = m1x2 – m1x
⇒ m1x + m2x = m1x2 + m2x1
⇒ (m1 + m2)x = m1x2 + m2x1
⇒ x = (m1x2 + m2x1) / (m1 + m2)
Now triangle ∆SPR is similar to triangle ∆TQR,
Therefore,
PS/TQ = PR/RQ
By using equations 4, 5, and 1, we know:
y – y1 / y2 – y = m1 / m2
⇒ m2y – m2y1 = m1y2 – m1y
⇒ m1y + m2y = m1y2 + m2y1
⇒ (m1 + m2)y = m1y2 + m2y1
⇒ y = (m1y2 + m2y1) / (m1 + m2)
Hence the coordinates of R(x,y) are:
R(x, y) = (m1x2 + m2x1) / (m1 + m2), (m1y2 + m2y1) / (m1 + m2)
As we had to calculate the midpoint, therefore, we keep the values both of m1 and m2 as same i.e.
For the mid-point we know by the definition of mid-point, m1 = m2 = 1.
(x, y) = ((1.x2 + 1.x1) / (1 + 1), (1.y2 + 1.y1) / (1 + 1))
x, y = (x2 + x1) / 2, (y2 + y1) / 2
How to find Mid Point?
To find the coordinates of the midpoint of any given line segment we can use the midpoint formula if the endpoints of the line segment are given. Consider the following example for the same.
Example: Find the coordinates of the midpoint of a line segment whose endpoints are (5, 6) and (-3, 4).
Solution:
As we know, the midpoint of a line segment is given by the formula:
Midpoint = ((x1+x2)/2 , (y1+y2)/2)
where (x1, y1) and (x2, y2) are the coordinates of the endpoints of the line segment.
Midpoint = ((5+(-3))/2, (6+4)/2)
⇒ Midpoint = (2/2, 10/2)
⇒ Midpoint = (1, 5)
Therefore, the coordinates of the midpoint of the line segment are (1, 5).
There are similar formulas to the midpoint formula, which are as follows:
- Section Formula
- Centroid Formula
Section Formula
Section Formula is used to find the coordinate of the point which divides the given line segment in the desired ratio. Let us assume the endpoints of a line segment are A and B with coordinates (x1, y1) and (x2, y2), and P be the point that divides the line segment joining the line AB in m:n. Then coordinate of P is given by:
P(x, y) = [(mx2 + nx1)/(m+n) , (my2 + ny1)/(m+n)]
Centroid Formula
The Centroid formula is used to find the center point of polygons and mathematically for triangles and quadrilaterals is given as follows:
Centroid of a Triangle Formula
The coordinates of the centroid of a triangle with vertices (x1, y1), (x2, y2), and (x3, y3) are:
C(x, y) = ((x1 + x2 + x3)/3, (y1 + y2 + y3)/3)

Centroid of Triangle
Centroid of a Quadrilateral Formula
The coordinates of the centroid of a quadrilateral with vertices (x1, y1), (x2, y2), (x3, y3), and (x4, y4) are:
C(x, y) = ((x1 + x2 + x3+ x4)/4, (y1 + y2 + y3+ y4)/4)

Centroid of Quadrilateral
Question 1: What is the mid-point of line segment AB where point A is at (6,8) and point B is (3,1)?
Solution:
Let the midpoint be M(xm, ym),
xm = (x1 + x2) / 2
x1 = 6, x2 = 3
Thus, xm = (6 + 3) / 2 = 9 / 2 = 4.5
ym = (y1 + y2) / 2
y1 = 8, y2 = 1
Thus, ym = (8 + 1) / 2 = 9 / 2 = 4.5
Hence the midpoint of line AB is (4.5, 4.5).
Question 2: What is the mid-point of line segment AB where point A is at (-6,4) and point B is (4,2)?
Solution:
Let the midpoint be M(xm, ym),
x1 = -6, x2 = 4, y1 = 4, y2 = 2
(xm, ym) = ((x1 + x2) / 2, (y1 + y2) / 2)
(xm, ym) = ((-6 + 4) / 2, (4 + 2) / 2)
(xm, ym) = ((-2) / 2, (6) / 2)
(xm, ym) = (-1, 3)
Hence the midpoint of line AB is (-1, 3).
Question 3: Find the value of p so that (–2, 2.5) is the midpoint between (p, 2) and (–1, 3).
Solution:
Let the midpoint be M(xm, ym) = (-2, 2.5) where,
x1 = -1, xm = -2
y-coordinate of the end point is already known as 2, hence we need to find only the x-coordinate
xm = (x1 + x2) / 2
-2 = (-1 + p) / 2
-4 = -1 + p
p = -3
Hence other end-point of line is (-3, 2).
Question 4: If the coordinates of the endpoints of a line segment are (3, 4) and (7, 8), find the distance between the midpoint of the line segment and the point (3, 4).
Solution:
Let A(3, 4) and B(7, 8) be the endpoints of the given line segment, and C is the midpoint of line segment AB.
Then using midpoint formula,
Coordinate of C = ( (3+7)/2 , (4+8)/2 ) = (5, 6)
Using Distance Formula
Distance = √{(x2 – x1)2 + (y2 – y1)2}
⇒ Distance = √{(3 – 5)2 + (4 – 6)2}
⇒ Distance =√{(-2)2 + (-2)2}
⇒ Distance =√8 = 2√2
Therefore, distance between midpoint of line segment and point (3, 4) is 2√2.
What is mid-point formula?
Mathematically Midpoint Formula is given as follows:
Midpoint = ((x1 + x2)/2 , (y1 + y2)/2)
What is significance of mid-point formula?
The mid-point formula is significant because it allows us to find the center point of any line segment on a Cartesian coordinate system.
What are applications of mid-point formula?
There are many use cases of the mid-point formula as in geometry we can use it for solutions and properties of triangles, polygons, and other shapes, in physics it has application in finding the center of mass as well.
Can mid-point formula be used for three or more points?
No, the mid-point formula can’t be used for three points as mid-point is defined for only two point. For three points we can use centroid formula if we want to find the coordinate of centroid for the triangle formed by the given three points.
How many midpoint does a segment have?
A segment has only one midpoint.
Share your thoughts in the comments
Please Login to comment...