What is Standard Deviation?
A scientific measure of dispersion that is widely used in statistical analysis of a given set of data is known as Standard Deviation. Another name for standard deviation is Root Mean Square Deviation. Standard Deviation is denoted by a Greek Symbol σ (sigma). Under this method, the deviation of values is taken from the arithmetic mean of the given set of data.
According to Spiegel, “The Standard Deviation is the square root of the arithmetic mean of the squares of all deviations. Deviations being measured from arithmetic mean of the items.”
Standard Deviation is considered to be the best way of determining the dispersion of a data set. It is because standard deviation takes into account every value of a data set along with its algebraic signs. Standard Deviation can be calculated in three different series; viz., Individual, Discrete, and Frequency Distribution or Continuous Series.
Methods of Calculating Standard Deviation in Discrete Series
- Actual Mean Method
- Direct Method
- Short-cut Method or Assumed Mean Method
- Step Deviation Method
1. Actual Mean Method:
In actual mean method, the standard deviation is calculated by taking deviations from the actual mean. The steps taken to determine standard deviation through the actual mean method are as follows:
Step 1: Determine the actual mean 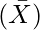 of the given observation, using the formula,
of the given observation, using the formula, 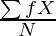
Step 2: Now, calculate the deviation of each item of the given series from the mean calculated in the first step; i.e., calculate 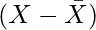 . Denote the deviations with x.
. Denote the deviations with x.
Step 3: After finding out the deviation, square these deviations and multiply them with their respective frequencies (f), and determine its total; i.e., ∑fx2
Step 4: Apply the following formula:
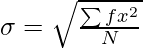
Where,
σ = Standard Deviation
∑fx2 = Sum total of the squared deviations multiplied by frequency
N = Number of pairs of observations
Example:
Calculate the Standard Deviation for the following data by using the Actual Mean Method.
Solution:
Arithmetic Mean 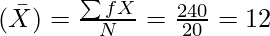
Standard Deviation (σ) = 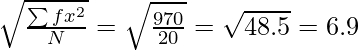
Standard Deviation = 6.9 or 7
2. Direct Method:
In Direct Method, there is no need to determine the deviation from the actual mean to calculate standard deviation. The steps taken to determine standard deviation through the direct method are as follows:
Step 1: First of all, calculate the actual mean 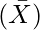 of the given observations, using the formula,
of the given observations, using the formula, 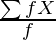
Step 2: Now square the observations and determine their total; i.e., ∑X2.
Step 3: Multiply frequency (f) by their respective X2 and determine the total; i.e., ∑fX2.
Step 4: Now, apply the following formula:
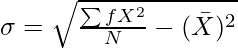
Or
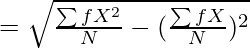
Where,
σ = Standard Deviation
∑fx2 = Sum total of the squared deviations multiplied by frequency
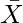 = Actual Mean
= Actual Mean
N = Number of Observations
Example:
Calculate the Standard Deviation for the following data by using the Direct Method.
Solution:
Arithmetic Mean 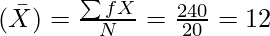
Standard Deviation (\sigma)=\sqrt{\frac{\sum{fX^2}}{N}-(\bar{X})^2}=\sqrt{\frac{3,850}{20}-(12)^2}
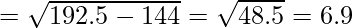
Standard Deviation = 6.9 or 7
3. Short-Cut Method or Assumed Mean Method:
Actual Mean can sometimes come in fractions, which can make the calculation of standard deviation complicated and difficult. In those cases, it is suggested to use Short-Cut Method to simplify the calculations. The steps taken to determine standard deviation through the assumed mean method are as follows:
Step 1: First of all, take any value of X in the series as Assumed Mean (A).
Step 2: Now determine the deviations of the items from an assumed mean and denote the deviations by d; i.e., d = X – A.
Step 3: Multiply the deviations calculated in the previous step by their respective frequencies and calculate their sum; i.e., ∑fd.
Step 4: Determine the square of the deviations, multiply it by their respective frequencies, and obtain the total; i.e., ∑fd2.
Step 5: Now, apply the following formula:
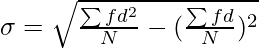
Or
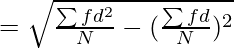
Where,
σ = Standard Deviation
∑fd = Sum total of deviations multiplied by frequencies
∑d2 = Sum total of the squared deviations multiplied by frequencies
N = Number of pairs of observations
Example:
Calculate the Standard Deviation for the following data by using the Assumed Mean Method.
Solution:
Arithmetic Mean 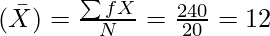
Standard Deviation (\sigma)=\sqrt{\frac{\sum{fd^2}}{N}-(\frac{\sum{fd}}{N})^2}=\sqrt{\frac{\sum{1,150}}{20}-(\frac{-60}{20})^2}
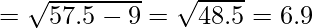
Standard Deviation = 6.9 or 7
4. Step Deviation Method:
This method is almost like the assumed mean method. The only difference in the formulas of both methods is that in the step deviation method, the deviations are divided by a common factor (C), and then the standard deviation is determined. The steps taken to determine standard deviation through the step deviation method are as follows:
Step 1: First of all take any value of X in the series as Assumed Mean (A).
Step 2: Now determine the deviations of the items from an assumed mean and denote the deviations by d; i.e., d = X – A.
Step 3: Divide these deviations by common factor (C) and obtain step deviations; i.e., 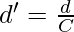
Step 4: Multiply the step deviations determined in the previous step by their respective frequencies, and obtain their total; i.e., 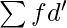
Step 5: Now determine the square of step deviations; i.e., 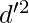
Step 6: Multiply the squared step deviations by their respective frequencies and determine the total to get 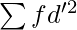
Step 7: Now, apply the following formula:
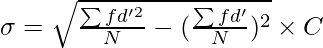
Where,
σ = Standard Deviation
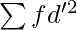 = Sum total of the squared step deviations multiplied by frequencies
= Sum total of the squared step deviations multiplied by frequencies
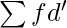 = Sum total of step deviations multiplied by frequencies
= Sum total of step deviations multiplied by frequencies
N = Number of pairs of observations
Example:
Calculate the Standard Deviation for the following data by using the Step-Deviation Method.
Solution:
Arithmetic Mean 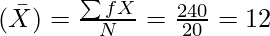
Standard Deviation 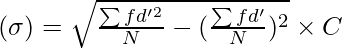
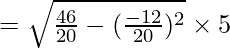
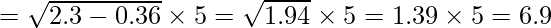
Standard Deviation = 6.9 or 7
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...