Merge two sorted arrays with O(1) extra space

Difficulty Level : Medium
Last Updated : 14 Oct, 2022

We are given two sorted arrays. We need to merge these two arrays such that the initial numbers (after complete sorting) are in the first array and the remaining numbers are in the second array. Extra space is allowed in O(1).

Example:

Input: ar1[] = {10};
       ar2[] = {2, 3};
Output: ar1[] = {2}
        ar2[] = {3, 10}  

Input: ar1[] = {1, 5, 9, 10, 15, 20};
       ar2[] = {2, 3, 8, 13};
Output: ar1[] = {1, 2, 3, 5, 8, 9}
        ar2[] = {10, 13, 15, 20}

This task is simple and O(m+n) if we are allowed to use extra space. But it becomes really complicated when extra space is not allowed and doesn’t look possible in less than O(m*n) worst-case time. Though further optimizations are possible
The idea is to begin from the last element of ar2[] and search it in ar1[]. If there is a greater element in ar1[], then we move the last element of ar1[] to ar2[]. To keep ar1[] and ar2[] sorted, we need to place the last element of ar2[] at the correct place in ar1[]. We can use Insertion Sort type of insertion for this.

1. Method 1

Algorithm:

1) Iterate through every element of ar2[] starting from last 
   element. Do following for every element ar2[i]
    a) Store last element of ar1[i]: last = ar1[i]
    b) Loop from last element of ar1[] while element ar1[j] is 
       greater than ar2[i].
          ar1[j+1] = ar1[j] // Move element one position ahead
          j--
    c) If any element of ar1[] was moved
          ar1[j+1] = ar2[i] 
          ar2[i] = last

In the above loop, elements in ar1[] and ar2[] are always kept sorted.

Below is the implementation of the above algorithm.

C++

// C++ program to merge two sorted arrays with O(1) extra
// space.
#include <bits/stdc++.h>
using namespace std;
 
// Merge ar1[] and ar2[] with O(1) extra space
void merge(int ar1[], int ar2[], int m, int n)
{
    // Iterate through all elements
    // of ar2[] starting from the last element
    for (int i = n - 1; i >= 0; i--) {
        // Find the smallest element greater than ar2[i].
        // Move all elements one position ahead till the
        // smallest greater element is not found */
        int j, last = ar1[m - 1];
        for (j = m - 2; j >= 0 && ar1[j] > ar2[i]; j--)
            ar1[j + 1] = ar1[j];
 
        // If there was a greater element
        if (last > ar2[i]) {
            ar1[j + 1] = ar2[i];
            ar2[i] = last;
        }
    }
}
 
// Driver program
int main()
{
    int ar1[] = { 1, 5, 9, 10, 15, 20 };
    int ar2[] = { 2, 3, 8, 13 };
    int m = sizeof(ar1) / sizeof(ar1[0]);
    int n = sizeof(ar2) / sizeof(ar2[0]);
    merge(ar1, ar2, m, n);
 
    cout << "After Merging \nFirst Array: ";
    for (int i = 0; i < m; i++)
        cout << ar1[i] << " ";
    cout << "\nSecond Array: ";
    for (int i = 0; i < n; i++)
        cout << ar2[i] << " ";
    return 0;
}

C

// C program to merge two sorted arrays with O(1) extra
// space.
#include <stdio.h>
 
// Merge ar1[] and ar2[] with O(1) extra space
void merge(int ar1[], int ar2[], int m, int n)
{
    // Iterate through all elements
    // of ar2[] starting from the last element
    for (int i = n - 1; i >= 0; i--) {
        // Find the smallest element greater than ar2[i].
        // Move all elements one position ahead till the
        // smallest greater element is not found */
        int j, last = ar1[m - 1];
        for (j = m - 2; j >= 0 && ar1[j] > ar2[i]; j--)
            ar1[j + 1] = ar1[j];
 
        // If there was a greater element
        if (last > ar2[i]) {
            ar1[j + 1] = ar2[i];
            ar2[i] = last;
        }
    }
}
 
// Driver program
int main()
{
    int ar1[] = { 1, 5, 9, 10, 15, 20 };
    int ar2[] = { 2, 3, 8, 13 };
    int m = sizeof(ar1) / sizeof(ar1[0]);
    int n = sizeof(ar2) / sizeof(ar2[0]);
    merge(ar1, ar2, m, n);
 
    printf("After Merging \nFirst Array: ");
    for (int i = 0; i < m; i++)
        printf("%d ", ar1[i]);
    printf("\nSecond Array: ");
    for (int i = 0; i < n; i++)
        printf("%d ", ar2[i]);
    return 0;
}
 
// This code is contributed by Aditya Kumar (adityakumar129)

Java

// Java program  to merge two
// sorted arrays with O(1) extra space.
 
import java.util.Arrays;
 
class Test
{
    static int arr1[] = new int[]{1, 5, 9, 10, 15, 20};
    static int arr2[] = new int[]{2, 3, 8, 13};
     
    static void merge(int m, int n)
    {
        // Iterate through all elements of ar2[] starting from
        // the last element
        for (int i=n-1; i>=0; i--)
        {
            /* Find the smallest element greater than ar2[i]. Move all
               elements one position ahead till the smallest greater
               element is not found */
            int j, last = arr1[m-1];
            for (j=m-2; j >= 0 && arr1[j] > arr2[i]; j--)
                arr1[j+1] = arr1[j];
      
            // If there was a greater element
            if (last > arr2[i])
            {
                arr1[j+1] = arr2[i];
                arr2[i] = last;
            }
        }
    }
     
    // Driver method to test the above function
    public static void main(String[] args)
    {
        merge(arr1.length,arr2.length);
        System.out.print("After Merging nFirst Array: ");
        System.out.println(Arrays.toString(arr1));
        System.out.print("Second Array:  ");
        System.out.println(Arrays.toString(arr2));
    }
}

Python3

# Python program to merge
# two sorted arrays
# with O(1) extra space.
 
# Merge ar1[] and ar2[]
# with O(1) extra space
def merge(ar1, ar2, m, n):
 
    # Iterate through all
    # elements of ar2[] starting from
    # the last element
    for i in range(n-1, -1, -1):
     
        # Find the smallest element
        # greater than ar2[i]. Move all
        # elements one position ahead
        # till the smallest greater
        # element is not found
        last = ar1[m-1]
        j=m-2
        while(j >= 0 and ar1[j] > ar2[i]):
            ar1[j+1] = ar1[j]
            j-=1
  
        # If there was a greater element
        if (last > ar2[i]):
         
            ar1[j+1] = ar2[i]
            ar2[i] = last
  
# Driver program
 
ar1 = [1, 5, 9, 10, 15, 20]
ar2 = [2, 3, 8, 13]
m = len(ar1)
n = len(ar2)
 
merge(ar1, ar2, m, n)
  
print("After Merging \nFirst Array:", end="")
for i in range(m):
    print(ar1[i] , " ", end="")
 
print("\nSecond Array: ", end="")
for i in range(n):
    print(ar2[i] , " ", end="")
 
# This code is contributed
# by Anant Agarwal.

C#

// C# program  to merge two
// sorted arrays with O(1) extra space.
using System;
 
// Java program  to merge two
// sorted arrays with O(1) extra space.
 
 
public class Test
{
    static int []arr1 = new int[]{1, 5, 9, 10, 15, 20};
    static int []arr2 = new int[]{2, 3, 8, 13};
     
    static void merge(int m, int n)
    {
        // Iterate through all elements of ar2[] starting from
        // the last element
        for (int i=n-1; i>=0; i--)
        {
            /* Find the smallest element greater than ar2[i]. Move all
            elements one position ahead till the smallest greater
            element is not found */
            int j, last = arr1[m-1];
            for (j=m-2; j >= 0 && arr1[j] > arr2[i]; j--)
                arr1[j+1] = arr1[j];
     
            // If there was a greater element
            if (last > arr2[i])
            {
                arr1[j+1] = arr2[i];
                arr2[i] = last;
            }
        }
    }
     
    // Driver method to test the above function
    public static void Main()
    {
        merge(arr1.Length,arr2.Length);
        Console.Write("After Merging \nFirst Array: ");
        for(int i =0; i< arr1.Length;i++){
            Console.Write(arr1[i]+" ");
        }
        Console.Write("\nSecond Array: ");
        for(int i =0; i< arr2.Length;i++){
            Console.Write(arr2[i]+" ");
        }
    }
}
 
/*This code is contributed by 29AjayKumar*/

PHP

<?php
// PHP program to merge two sorted arrays with O(1) extra space.
  
// Merge ar1[] and ar2[] with O(1) extra space
function merge(&$ar1, &$ar2, $m, $n)
{
    // Iterate through all elements of ar2[] starting from
    // the last element
    for ($i = $n-1; $i >= 0; $i--)
    {
        /* Find the smallest element greater than ar2[i]. Move all
           elements one position ahead till the smallest greater
           element is not found */
        $last = $ar1[$m-1];
        for ($j = $m-2; $j >= 0 && $ar1[$j] > $ar2[$i]; $j--)
            $ar1[$j+1] = $ar1[$j];
  
        // If there was a greater element
        if ($last > $ar2[$i])
        {
            $ar1[$j+1] = $ar2[$i];
            $ar2[$i] = $last;
        }
    }
}
  
// Driver program
 
$ar1 = array(1, 5, 9, 10, 15, 20);
$ar2 = array(2, 3, 8, 13);
$m = sizeof($ar1)/sizeof($ar1[0]);
$n = sizeof($ar2)/sizeof($ar2[0]);
merge($ar1, $ar2, $m, $n);
 
echo "After Merging \nFirst Array: ";
for ($i=0; $i<$m; $i++)
    echo $ar1[$i] . " ";
echo "\nSecond Array: ";
for ($i=0; $i<$n; $i++)
    echo $ar2[$i] ." ";
return 0;
?>

Javascript

<script>
 
// Javascript program to merge two
// sorted arrays with O(1) extra space.
 
    let arr1=[1, 5, 9, 10, 15, 20];
    let arr2=[2, 3, 8, 13];
     
    function merge(m,n)
    {
        // Iterate through all elements of ar2[] starting from
        // the last element
        for (let i=n-1; i>=0; i--)
        {
            /* Find the smallest element greater than ar2[i]. Move all
               elements one position ahead till the smallest greater
               element is not found */
            let j, last = arr1[m-1];
            for (j=m-2; j >= 0 && arr1[j] > arr2[i]; j--)
                arr1[j+1] = arr1[j];
       
            // If there was a greater element
            if (last > arr2[i])
            {
                arr1[j+1] = arr2[i];
                arr2[i] = last;
            }
        }
    }
     
    // Driver method to test the above function
    merge(arr1.length,arr2.length);
    document.write("After Merging <br>First Array: ");
    for(let i=0;i<arr1.length;i++)
    {
        document.write(arr1[i]+" ");
    }
    document.write("<br>Second Array:  ");
    for(let i=0;i<arr2.length;i++)
    {
        document.write(arr2[i]+" ");
    }
     
     
    //  This code is contributed by avanitrachhadiya2155
     
</script>

Output

After Merging 
First Array: 1 2 3 5 8 9 
Second Array: 10 13 15 20

Time Complexity: The worst-case time complexity of code/algorithm is O(m*n). The worst case occurs when all elements of ar1[] are greater than all elements of ar2[].

Illustration:

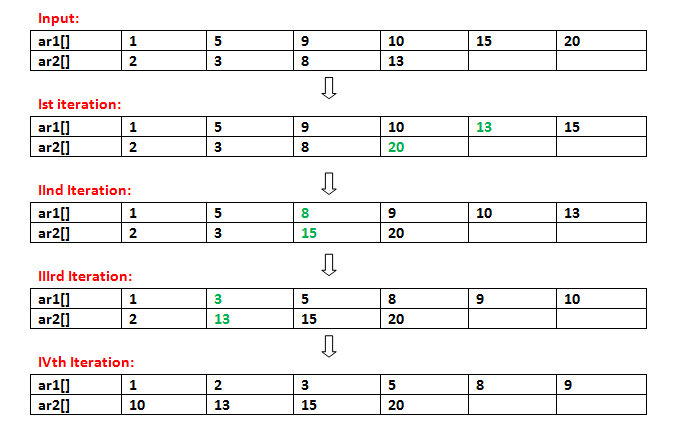
<!— Initial Arrays:
ar1[] = {1, 5, 9, 10, 15, 20};
ar2[] = {2, 3, 8, 13};
After First Iteration:
ar1[] = {1, 5, 9, 10, 13, 15};
ar2[] = {2, 3, 8, 20};
// 20 is moved from ar1[] to ar2[]
// 13 from ar2[] is inserted in ar1[]
After Second Iteration:
ar1[] = {1, 5, 8, 9, 10, 13};
ar2[] = {2, 3, 15, 20};
// 15 is moved from ar1[] to ar2[]
// 8 from ar2[] is inserted in ar1[]
After Third Iteration:
ar1[] = {1, 3, 5, 8, 9, 10};
ar2[] = {2, 13, 15, 20};
// 13 is moved from ar1[] to ar2[]
// 3 from ar2[] is inserted in ar1[]
After Fourth Iteration:
ar1[] = {1, 2, 3, 5, 8, 9};
ar2[] = {10, 13, 15, 20};
// 10 is moved from ar1[] to ar2[]
// 2 from ar2[] is inserted in ar1[]
—!>

Method 2:

The solution can be further optimized by observing that while traversing the two sorted arrays parallelly, if we encounter the jth second array element is smaller than ith first array element, then jth element is to be included and replace some kth element in the first array. This observation helps us with the following algorithm

Algorithm

1) Initialize i,j,k as 0,0,n-1 where n is size of arr1 
2) Iterate through every element of arr1 and arr2 using two pointers i and j respectively
    if arr1[i] is less than arr2[j]
        increment i
    else
        swap the arr2[j] and arr1[k]
        increment j and decrement k

3) Sort both arr1 and arr2

Below is the implementation of the above algorithm

C++

// CPP program for the above approach
#include <bits/stdc++.h>
using namespace std;
 
// Function to merge two arrays
void merge(int arr1[], int arr2[], int n, int m)
{
    int i = 0, j = 0, k = n - 1;
   
    // Until i less than equal to k
    // or j is less than m
    while (i <= k && j < m) {
        if (arr1[i] < arr2[j])
            i++;
        else {
            swap(arr2[j++], arr1[k--]);
        }
    }
   
    // Sort first array
    sort(arr1, arr1 + n);
   
    // Sort second array
    sort(arr2, arr2 + m);
}
 
// Driver Code
int main()
{
 
    int ar1[] = { 1, 5, 9, 10, 15, 20 };
    int ar2[] = { 2, 3, 8, 13 };
    int m = sizeof(ar1) / sizeof(ar1[0]);
    int n = sizeof(ar2) / sizeof(ar2[0]);
    merge(ar1, ar2, m, n);
 
    cout << "After Merging \nFirst Array: ";
    for (int i = 0; i < m; i++)
        cout << ar1[i] << " ";
    cout << "\nSecond Array: ";
    for (int i = 0; i < n; i++)
        cout << ar2[i] << " ";
    return 0;
}

Java

// Java program for the above approach
import java.util.Arrays;
import java.util.Collections;
 
class GFG {
    static int arr1[] = new int[] { 1, 5, 9, 10, 15, 20 };
    static int arr2[] = new int[] { 2, 3, 8, 13 };
 
    // Function to merge two arrays
    static void merge(int m, int n)
    {
        int i = 0, j = 0, k = m - 1;
        while (i <= k && j < n) {
            if (arr1[i] < arr2[j])
                i++;
            else {
                int temp = arr2[j];
                arr2[j] = arr1[k];
                arr1[k] = temp;
                j++;
                k--;
            }
        }
        Arrays.sort(arr1);
        Arrays.sort(arr2);
    }
 
    public static void main(String[] args)
    {
        merge(arr1.length, arr2.length);
        System.out.print("After Merging \nFirst Array: ");
        System.out.println(Arrays.toString(arr1));
        System.out.print("Second Array:  ");
        System.out.println(Arrays.toString(arr2));
    }
}

Python3

# Python program for the above approach
arr1 = [1, 5, 9, 10, 15, 20]
arr2 = [2, 3, 8, 13]
 
# Function to merge two arrays
 
 
def merge(n, m):
    i = 0
    j = 0
    k = n - 1
    while (i <= k and j < m):
        if (arr1[i] < arr2[j]):
            i += 1
        else:
            temp = arr2[j]
            arr2[j] = arr1[k]
            arr1[k] = temp
            j += 1
            k -= 1
 
    arr1.sort()
    arr2.sort()
 
 
# Driver code
if __name__ == '__main__':
    merge(len(arr1), len(arr2))
    print("After Merging \nFirst Array: ")
    print(','.join(str(x) for x in arr1))
    print("Second Array:  ")
    print(','.join(str(x) for x in arr2))
 
# This code is contributed by gauravrajput1

C#

// C# program for the above approach
using System;
 
public class GFG {
  static int []arr1 ={ 1, 5, 9, 10, 15, 20 };
 
  static int []arr2 = { 2, 3, 8, 13 };
 
  // Function to merge two arrays
  static void merge(int m, int n)
  {
    int i = 0, j = 0, k = n - 1;
    while (i <= k && j < m) {
      if (arr1[i] < arr2[j])
        i++;
      else {
        int temp = arr2[j];
        arr2[j] = arr1[k];
        arr1[k] = temp;
        j++;
        k--;
      }
    }
    Array.Sort(arr1);
    Array.Sort(arr2);
  }
 
  public static void Main(String[] args)
  {
    merge(arr1.Length, arr2.Length);
    Console.Write("After Merging \nFirst Array: ");
    foreach(int i in arr1){
      Console.Write(i+" ");
    }
    Console.Write("\nSecond Array:  ");
    foreach(int i in arr2){
      Console.Write(i+" ");
    }
  }
}
 
// This code is contributed by gauravrajput1

Javascript

<script>
// javascript program for the above approach
var arr1 = [ 1, 5, 9, 10, 15, 20 ];
    var arr2 = [ 2, 3, 8, 13 ];
 
    // Function to merge two arrays
    function merge(m , n) {
        var i = 0, j = 0, k = n - 1;
        while (i <= k && j < m) {
            if (arr1[i] < arr2[j])
                i++;
            else {
                var temp = arr2[j];
                arr2[j] = arr1[k];
                arr1[k] = temp;
                j++;
                k--;
            }
        }
        arr1.sort((a,b)=>a-b);
        arr2.sort((a,b)=>a-b);
    }
 
     
        merge(arr1.length, arr2.length);
        document.write("After Merging <br/>First Array:<br/> ");
        for(var a of arr1)
        document.write(a+" ");
        document.write("<br/>Second Array: <br/> ");
        for(var a of arr2)
        document.write(a+" ");
 
// This code is contributed by gauravrajput1
</script>

Output

After Merging 
First Array: 1 2 3 5 8 9 
Second Array: 10 13 15 20

Complexities:
Time Complexity: The time complexity while traversing the arrays in while loop is O(n+m) in worst case and sorting is O(nlog(n) + mlog(m)). So overall time complexity of the code becomes O((n+m)log(n+m)).
Space Complexity: As the function doesn’t use any extra array for any operations, the space complexity is O(1).

Method 3:
Algorithm:

1) Initialize i with 0
2) Iterate while loop until last element of array 1 is greater than first element of array 2
          if arr1[i] greater than first element of arr2
              swap arr1[i] with arr2[0]
              sort arr2
          incrementing i

C++

#include<iostream>
#include<bits/stdc++.h>
using namespace std;
 
void merge(int arr1[], int arr2[], int n, int m) {
        int i=0;
        // while loop till last element of array 1(sorted) is greater than
          // first element of array 2(sorted)
        while(arr1[n-1]>arr2[0])
        {
            if(arr1[i]>arr2[0])
            {
                // swap arr1[i] with first element
                  // of arr2 and sorting the updated
                // arr2(arr1 is already sorted)
                swap(arr1[i],arr2[0]);
                sort(arr2,arr2+m);
            }
            i++;
        }
    }
 
int main()
{
 
    int ar1[] = { 1, 5, 9, 10, 15, 20 };
    int ar2[] = { 2, 3, 8, 13 };
    int m = sizeof(ar1) / sizeof(ar1[0]);
    int n = sizeof(ar2) / sizeof(ar2[0]);
    merge(ar1, ar2, m, n);
 
    cout << "After Merging \nFirst Array: ";
    for (int i = 0; i < m; i++)
        cout << ar1[i] << " ";
    cout << "\nSecond Array: ";
    for (int i = 0; i < n; i++)
        cout << ar2[i] << " ";
    return 0;
 
}

Java

import java.io.*;
import java.util.Arrays;
import java.util.Collections;
 
class GFG{
 
static int arr1[] = new int[]{ 1, 5, 9, 10, 15, 20 };
static int arr2[] = new int[]{ 2, 3, 8, 13 };
 
static void merge(int n, int m)
{
    int i = 0;
    int temp = 0;
     
    // While loop till last element
    // of array 1(sorted)
    // is greater than first element
    // of array 2(sorted)
    while (arr1[n - 1] > arr2[0])
    {
        if (arr1[i] > arr2[0])
        {
             
            // Swap arr1[i] with first element
            // of arr2 and sorting the updated
            // arr2(arr1 is already sorted)
            // swap(arr1[i],arr2[0]);
            temp = arr1[i];
            arr1[i] = arr2[0];
            arr2[0] = temp;
            Arrays.sort(arr2);
        }
        i++;
    }
}
 
// Driver code
public static void main(String[] args)
{
    merge(arr1.length, arr2.length);
 
    System.out.print("After Merging \nFirst Array: ");
    System.out.println(Arrays.toString(arr1));
     
    System.out.print("Second Array:  ");
    System.out.println(Arrays.toString(arr2));
}
}
 
// This code is contributed by Aakash Tiwari(nighteagle)

Python3

arr1 = [1, 5, 9, 10, 15, 20 ];
arr2 =[ 2, 3, 8, 13 ];
 
def merge(n, m):
    i = 0;
    temp = 0;
 
    # While loop till last element
    # of array 1(sorted)
    # is greater than first element
    # of array 2(sorted)
    while (arr1[n - 1] > arr2[0]):
        if (arr1[i] > arr2[0]):
 
            # Swap arr1[i] with first element
            # of arr2 and sorting the updated
            # arr2(arr1 is already sorted)
            # swap(arr1[i],arr2[0]);
            temp = arr1[i];
            arr1[i] = arr2[0];
            arr2[0] = temp;
            arr2.sort();
         
        i+=1;
     
 
 
# Driver code
if __name__ == '__main__':
    merge(len(arr1), len(arr2));
 
    print("After Merging \nFirst Array: ");
    print((arr1));
 
    print("Second Array:  ");
    print((arr2));
 
 
# This code contributed by gauravrajput1

C#

using System;
 
public class GFG {
 
    static int []arr1 = new int[] { 1, 5, 9, 10, 15, 20 };
    static int []arr2 = new int[] { 2, 3, 8, 13 };
 
    static void merge(int n, int m) {
        int i = 0;
        int temp = 0;
 
        // While loop till last element
        // of array 1(sorted)
        // is greater than first element
        // of array 2(sorted)
        while (arr1[n - 1] > arr2[0]) {
            if (arr1[i] > arr2[0]) {
 
                // Swap arr1[i] with first element
                // of arr2 and sorting the updated
                // arr2(arr1 is already sorted)
                // swap(arr1[i],arr2[0]);
                temp = arr1[i];
                arr1[i] = arr2[0];
                arr2[0] = temp;
                Array.Sort(arr2);
            }
            i++;
        }
    }
 
    // Driver code
    public static void Main(String[] args) {
        merge(arr1.Length, arr2.Length);
 
        Console.Write("After Merging \nFirst Array: ");
        foreach(int i in arr1)
            Console.Write(i+" ");
        Console.Write("\nSecond Array:  ");
        foreach(int i in arr2)
            Console.Write(i+" ");
    }
}
 
// This code is contributed by gauravrajput1

Javascript

<script>
    var arr1 =  [1, 5, 9, 10, 15, 20 ];
    var arr2 =[2, 3, 8, 13 ];
 
    function merge(n , m) {
        var i = 0;
        var temp = 0;
 
        // While loop till last element
        // of array 1(sorted)
        // is greater than first element
        // of array 2(sorted)
        while (arr1[n - 1] > arr2[0]) {
            if (arr1[i] > arr2[0]) {
 
                // Swap arr1[i] with first element
                // of arr2 and sorting the updated
                // arr2(arr1 is already sorted)
                // swap(arr1[i],arr2[0]);
                temp = arr1[i];
                arr1[i] = arr2[0];
                arr2[0] = temp;
                arr2.sort((a,b)=>a-b);
            }
            i++;
        }
    }
 
    // Driver code
        merge(arr1.length, arr2.length);
 
        document.write("After Merging <br\>First Array: ");
        document.write(arr1.toString());
 
        document.write("<br\>Second Array:  ");
        document.write(arr2.toString());
 
// This code is contributed by umadevi9616
</script>

Output

After Merging 
First Array: 1 2 3 5 8 9 
Second Array: 10 13 15 20

Efficiently merging two sorted arrays with O(1) extra space

Method 4: Let the length of the shorter array be ‘m’ and the larger array be ‘n’

Step 1: Select the shorter array and find the index at which partition should be done. Similar to this https://www.geeksforgeeks.org/median-of-two-sorted-arrays-of-different-sizes/

Step 1: Partition the shorter array at its median (l1).

Step 2: Select the first n-l1 elements from the second array.

Step 3: Compare the border elements i.e.

if l1 < r2 and l2 < r2 we have found the index

else if l1 > r2 we have to search in the left subarray

else we have to search in the right subarray

NOTE : This step will store all the smallest elements in the shorter array.

Step 2: Swap all the elements right to the index(i) of the shorter array with the first n-i elements of the larger array.

Step 3: Sort both the arrays.

::::: if len(arr1) > len(arr2) all the smallest elements are stored in arr2 so we have to move all the elements in arr1 since we have to print arr1 first.

Step 4: Rotate the larger array (arr1) m times counter-clockwise.

Step 5: Swap the first m elements of both the arrays.

C++

#include <bits/stdc++.h>
using namespace std;
 
void swap(int& a, int& b)
{
    int temp = a;
    a = b;
    b = temp;
}
 
void rotate(int a[], int n, int idx)
{
    int i;
    for (i = 0; i < idx / 2; i++)
        swap(a[i], a[idx - 1 - i]);
    for (i = idx; i < (n + idx) / 2; i++)
        swap(a[i], a[n - 1 - (i - idx)]);
    for (i = 0; i < n / 2; i++)
        swap(a[i], a[n - 1 - i]);
}
 
void sol(int a1[], int a2[], int n, int m)
{
    int l = 0, h = n - 1, idx = 0;
    //---------------------------------------------------------
    while (l <= h) {
        // select the median of the remaining subarray
        int c1 = (l + h) / 2;
        // select the first elements from the larger array
        // equal to the size of remaining portion to the
        // right of the smaller array
        int c2 = n - c1 - 1;
        int l1 = a1[c1];
        int l2 = a2[c2 - 1];
        int r1 = c1 == n - 1 ? INT_MAX : a1[c1 + 1];
        int r2 = c2 == m ? INT_MAX : a2[c2];
        // compare the border elements and check for the
        // target index
        if (l1 > r2) {
            h = c1 - 1;
            if (h == -1)
                idx = 0;
        }
        else if (l2 > r1) {
            l = c1 + 1;
            if (l == n - 1)
                idx = n;
        }
        else {
            idx = c1 + 1;
            break;
        }
    }
 
    for (int i = idx; i < n; i++)
        swap(a1[i], a2[i - idx]);
 
    sort(a1, a1 + n);
 
    sort(a2, a2 + m);
}
 
void merge(int arr1[], int arr2[], int n, int m)
{
    // code here
    if (n > m) {
        sol(arr2, arr1, m, n);
        rotate(arr1, n, n - m);
 
        for (int i = 0; i < m; i++)
            swap(arr2[i], arr1[i]);
    }
    else {
        sol(arr1, arr2, n, m);
    }
}
 
int main()
{
 
    int ar1[] = { 1, 5, 9, 10, 15, 20 };
    int ar2[] = { 2, 3, 8, 13 };
    int m = sizeof(ar1) / sizeof(ar1[0]);
    int n = sizeof(ar2) / sizeof(ar2[0]);
    merge(ar1, ar2, m, n);
 
    cout << "After Merging \nFirst Array: ";
    for (int i = 0; i < m; i++)
        cout << ar1[i] << " ";
    cout << "\nSecond Array: ";
    for (int i = 0; i < n; i++)
        cout << ar2[i] << " ";
    return 0;
}

Java

// Java program for the above approach
import java.util.*;
 
class GFG
{
 
static void swap(int a, int b)
{
    int temp = a;
    a = b;
    b = temp;
}
 
static void rotate(int a[], int n, int idx)
{
    int i;
    for (i = 0; i < idx / 2; i++)
        swap(a[i], a[idx - 1 - i]);
    for (i = idx; i < (n + idx) / 2; i++)
        swap(a[i], a[n - 1 - (i - idx)]);
    for (i = 0; i < n / 2; i++)
        swap(a[i], a[n - 1 - i]);
}
 
static void sol(int a1[], int a2[], int n, int m)
{
    int l = 0, h = n - 1, idx = 0;
    //---------------------------------------------------------
    while (l <= h) {
        // select the median of the remaining subarray
        int c1 = (int)(l + h) / 2;
        // select the first elements from the larger array
        // equal to the size of remaining portion to the
        // right of the smaller array
        int c2 = n - c1 - 1;
        int l1 = a1[c1];
        int l2 = a2[c2 - 1];
        int r1 = (c1 == n - 1) ? Integer.MAX_VALUE : a1[c1 + 1];
        int r2 = (c2 == m) ? Integer.MAX_VALUE : a2[c2];
 
        // compare the border elements and check for the
        // target index
        if (l1 > r2) {
            h = c1 - 1;
            if (h == -1)
                idx = 0;
        }
        else if (l2 > r1) {
            l = c1 + 1;
            if (l == n - 1)
                idx = n;
        }
        else {
            idx = c1 + 1;
            break;
        }
    }
 
    for (int i = idx; i < n; i++)
        swap(a1[i], a2[i - idx]);
 
    Arrays.sort(a1);
 
    Arrays.sort(a2);
}
 
static void merge(int arr1[], int arr2[], int n, int m)
{
    // code here
    if (n > m) {
        sol(arr2, arr1, m, n);
        rotate(arr1, n, n - m);
 
        for (int i = 0; i < m; i++)
            swap(arr2[i], arr1[i]);
    }
    else {
        sol(arr1, arr2, n, m);
    }
}
 
// Driver Code
public static void main (String[] args)
{
    int ar1[] = { 1, 5, 9, 10, 15, 20 };
    int ar2[] = { 2, 3, 8, 13 };
    int m = ar1.length;
    int n = ar2.length;
    merge(ar1, ar2, m, n);
 
    System.out.print("After Merging \nFirst Array: ");
    for (int i = 0; i < m; i++)
        System.out.print(ar1[i] + " ");
    System.out.print("\nSecond Array: ");
    for (int i = 0; i < n; i++)
        System.out.print(ar2[i] + " ");
 
}
}
 
// This code is contributed by sanjoy_62.

Python3

# Python program to merge
# two sorted arrays
# with O(1) extra space.
 
# Merge ar1[] and ar2[]
# with O(1) extra space
 
 
def rotate(a, n, idx):
    for i in range((int)(idx/2)):
        a[i], a[idx-1-i] = a[idx-1-i], a[i]
    for i in range(idx, (int)((n+idx)/2)):
        a[i], a[n-1-(i-idx)] = a[n-1-(i-idx)], a[i]
    for i in range((int)(n/2)):
        a[i], a[n-1-i] = a[n-1-i], a[i]
 
 
def sol(a1, a2, n, m):
    l = 0
    h = n-1
    idx = 0
    while (l <= h):
        c1 = (int)((l+h)/2)
        c2 = n-c1-1
        l1 = a1[c1]
        l2 = a2[c2-1]
        r1 = sys.maxint if c1 == n-1 else a1[c1+1]
        r2 = sys.maxint if c2 == m else a2[c2]
        if l1 > r2:
            h = c1-1
            if h == -1:
                idx = 0
        elif l2 > r1:
            l = c1+1
            if l == n-1:
                idx = n
        else:
            idx = c1+1
            break
    for i in range(idx, n):
        a1[i], a2[i-idx] = a2[i-idx], a1[i]
 
    a1.sort()
    a2.sort()
 
 
def merge(a1, a2, n, m):
    if n > m:
        sol(a2, a1, m, n)
        rotate(a1, n, n-m)
        for i in range(m):
            a1[i], a2[i] = a2[i], a1[i]
    else:
        sol(a1, a2, n, m)
# Driver program
 
 
ar1 = [1, 5, 9, 10, 15, 20]
ar2 = [2, 3, 8, 13]
m = len(ar1)
n = len(ar2)
 
merge(ar1, ar2, m, n)
 
print("After Merging \nFirst Array:", end="")
for i in range(m):
    print(ar1[i], " ", end="")
print("\nSecond Array: ", end="")
for i in range(n):
    print(ar2[i], " ", end="")
# This code is contributed
# by Aditya Anand.

C#

// C# program for the above approach
using System;
using System.Collections.Generic;
 
public class GFG {
 
    static void swap(int a, int b) {
        int temp = a;
        a = b;
        b = temp;
    }
 
    static void rotate(int []a, int n, int idx) {
        int i;
        for (i = 0; i < idx / 2; i++)
            swap(a[i], a[idx - 1 - i]);
        for (i = idx; i < (n + idx) / 2; i++)
            swap(a[i], a[n - 1 - (i - idx)]);
        for (i = 0; i < n / 2; i++)
            swap(a[i], a[n - 1 - i]);
    }
 
    static void sol(int []a1, int []a2, int n, int m) {
        int l = 0, h = n - 1, idx = 0;
        // ---------------------------------------------------------
        while (l <= h) {
            // select the median of the remaining subarray
            int c1 = (int) (l + h) / 2;
            // select the first elements from the larger array
            // equal to the size of remaining portion to the
            // right of the smaller array
            int c2 = n - c1 - 1;
            int l1 = a1[c1];
            int l2 = a2[c2 - 1];
            int r1 = (c1 == n - 1) ? int.MaxValue : a1[c1 + 1];
            int r2 = (c2 == m) ? int.MaxValue : a2[c2];
 
            // compare the border elements and check for the
            // target index
            if (l1 > r2) {
                h = c1 - 1;
                if (h == -1)
                    idx = 0;
            } else if (l2 > r1) {
                l = c1 + 1;
                if (l == n - 1)
                    idx = n;
            } else {
                idx = c1 + 1;
                break;
            }
        }
 
        for (int i = idx; i < n; i++)
            swap(a1[i], a2[i - idx]);
 
        Array.Sort(a1);
 
        Array.Sort(a2);
    }
 
    static void merge(int []arr1, int []arr2, int n, int m) {
        // code here
        if (n > m) {
            sol(arr2, arr1, m, n);
            rotate(arr1, n, n - m);
 
            for (int i = 0; i < m; i++)
                swap(arr2[i], arr1[i]);
        } else {
            sol(arr1, arr2, n, m);
        }
    }
 
    // Driver Code
    public static void Main(String[] args) {
        int []ar1 = { 1, 5, 9, 10, 15, 20 };
        int []ar2 = { 2, 3, 8, 13 };
        int m = ar1.Length;
        int n = ar2.Length;
        merge(ar1, ar2, m, n);
 
        Console.Write("After Merging \nFirst Array: ");
        for (int i = 0; i < m; i++)
            Console.Write(ar1[i] + " ");
        Console.Write("\nSecond Array: ");
        for (int i = 0; i < n; i++)
            Console.Write(ar2[i] + " ");
 
    }
}
 
 
// This code contributed by gauravrajput1

Javascript

<script>
// javascript program for the above approach
 
    function swap(a , b) {
        var temp = a;
        a = b;
        b = temp;
    }
 
    function rotate(a , n , idx) {
        var i;
        for (i = 0; i < idx / 2; i++)
        {
            var temp  =a[i]
            a[i]= a[idx - 1 - i];
            a[idx - 1 - i] = temp;
        }
     
        for (i = idx; i < (n + idx) / 2; i++)
        {
            var temp  =a[i]
            a[i]= a[n - 1 - (i - idx)];
            a[n - 1 - (i - idx)] = temp;
        }
 
        for (i = 0; i < n / 2; i++)
        {
            var temp  =a[i]
               a[i]= a[n - 1 - i];
            a[n - 1 - i] = temp;
        }
    }
 
    function sol(a1 , a2 , n , m) {
        var l = 0, h = n - 1, idx = 0;
        // ---------------------------------------------------------
        while (l <= h)
        {
         
            // select the median of the remaining subarray
            var c1 = parseInt( (l + h) / 2);
             
            // select the first elements from the larger array
            // equal to the size of remaining portion to the
            // right of the smaller array
            var c2 = n - c1 - 1;
            var l1 = a1[c1];
            var l2 = a2[c2 - 1];
            var r1 = (c1 == n - 1) ? Number.MAX_VALUE : a1[c1 + 1];
            var r2 = (c2 == m) ? Number.MAX_VALUE : a2[c2];
 
            // compare the border elements and check for the
            // target index
            if (l1 > r2) {
                h = c1 - 1;
                if (h == -1)
                    idx = 0;
            } else if (l2 > r1) {
                l = c1 + 1;
                if (l == n - 1)
                    idx = n;
            } else {
                idx = c1 + 1;
                break;
            }
        }
 
        for (i = idx; i < n; i++)
         {
            var temp  =a1[i]
            a1[i]= a2[i - idx];
            a2[i - idx] = temp;
        }   
 
        a1.sort((a,b)=>a-b);
 
        a2.sort((a,b)=>a-b);
    }
 
    function merge(arr1 , arr2 , n , m) {
        // code here
        if (n > m) {
            sol(arr2, arr1, m, n);
            rotate(arr1, n, n - m);
 
            for (i = 0; i < m; i++)
            {
        var temp  =arr2[i]
        arr2[i]= arr1[i];
        arr1[i] = temp;
        }
                 
        } else {
            sol(arr1, arr2, n, m);
        }
    }
 
    // Driver Code
     
        var ar1 = [ 1, 5, 9, 10, 15, 20 ];
        var ar2 = [ 2, 3, 8, 13 ];
        var m = ar1.length;
        var n = ar2.length;
        merge(ar1, ar2, m, n);
 
        document.write("After Merging \nFirst Array: ");
        for (i = 0; i < m; i++)
            document.write(ar1[i] + " ");
        document.write("\nSecond Array: ");
        for (i = 0; i < n; i++)
            document.write(ar2[i] + " ");
 
// This code is contributed by gauravrajput1
</script>

Output

After Merging 
First Array: 1 2 3 5 8 9 
Second Array: 10 13 15 20

Time Complexity: O(max(nlogn, mlogm))

Method-5 [Insertion Sort with Simultaneous Merge]

Approach:
1. sort list 1 by always comparing with head/first of list 2 and swapping if required
2. after each head/first swap, perform insertion of the swapped element into correct position in list 2 which will eventually sort list 2 at the end.
For every swapped item from list 1, perform insertion sort in list 2 to find its correct position so that when list 1 is sorted, list 2 is also sorted.

C++

#include <bits/stdc++.h>
using namespace std;
 
void merge(int arr1[], int arr2[], int n, int m)
{
    // two pointer to iterate
    int i = 0;
    int j = 0;
    while (i < n && j < m) {
        // if arr1[i] <= arr2[j] then both array is already
        // sorted
        if (arr1[i] <= arr2[j]) {
            i++;
        }
        else if (arr1[i] > arr2[j]) {
            // if arr1[i]>arr2[j] then first we swap both
            // element so that arr1[i] become smaller means
            // arr1[] become sorted then we check that
            // arr2[j] is smaller than all other element in
            // right side of arr2[j] if arr2[] is not sorted
            // then we linearly do sorting
            // means while adjacent element are less than
            // new arr2[j] we do sorting like by changing
            // position of element by shifting one position
            // toward left
            swap(arr1[i], arr2[j]);
            i++;
            if (j < m - 1 && arr2[j + 1] < arr2[j]) {
                int temp = arr2[j];
                int tempj = j + 1;
                while (arr2[tempj] < temp && tempj < m) {
                    arr2[tempj - 1] = arr2[tempj];
                    tempj++;
                }
                arr2[tempj - 1] = temp;
            }
        }
    }
}
 
int main()
{
 
    int ar1[] = { 1, 5, 9, 10, 15, 20 };
    int ar2[] = { 2, 3, 8, 13 };
    int m = sizeof(ar1) / sizeof(ar1[0]);
    int n = sizeof(ar2) / sizeof(ar2[0]);
    merge(ar1, ar2, m, n);
 
    cout << "After Merging \nFirst Array: ";
    for (int i = 0; i < m; i++)
        cout << ar1[i] << " ";
    cout << "\nSecond Array: ";
    for (int i = 0; i < n; i++)
        cout << ar2[i] << " ";
    return 0;
}

Java

import java.util.*;
class GFG{
 
static void merge(int arr1[], int arr2[], int n, int m)
{
    // two pointer to iterate
    int i = 0;
    int j = 0;
    while (i < n && j < m)
    {
       
        // if arr1[i] <= arr2[j] then both array is already
        // sorted
        if (arr1[i] <= arr2[j]) {
            i++;
        }
        else if (arr1[i] > arr2[j])
        {
           
            // if arr1[i]>arr2[j] then first we swap both
            // element so that arr1[i] become smaller means
            // arr1[] become sorted then we check that
            // arr2[j] is smaller than all other element in
            // right side of arr2[j] if arr2[] is not sorted
            // then we linearly do sorting
            // means while adjacent element are less than
            // new arr2[j] we do sorting like by changing
            // position of element by shifting one position
            // toward left
            int t = arr1[i];
            arr1[i] = arr2[j];
            arr2[j] = t;
            i++;
            if (j < m - 1 && arr2[j + 1] < arr2[j]) {
                int temp = arr2[j];
                int tempj = j + 1;
                while (tempj<m && arr2[tempj] < temp && tempj < m) {
                    arr2[tempj - 1] = arr2[tempj];
                    tempj++;
                }
                arr2[tempj - 1] = temp;
            }
        }
    }
}
 
public static void main(String[] args)
{
 
    int ar1[] = { 1, 5, 9, 10, 15, 20 };
    int ar2[] = { 2, 3, 8, 13 };
    int m = ar1.length;
    int n =ar2.length;
    merge(ar1, ar2, m, n);
 
    System.out.print("After Merging \nFirst Array: ");
    for (int i = 0; i < m; i++)
        System.out.print(ar1[i]+ " ");
    System.out.print("\nSecond Array: ");
    for (int i = 0; i < n; i++)
        System.out.print(ar2[i]+ " ");
}
}
 
// This code is contributed by gauravrajput1

Python3

# code contributed by mahee96
 
# "Insertion sort of list 2 with swaps from list 1"
#
# swap elements to get list 1 correctly, meanwhile
# place the swapped item in correct position of list 2
# eventually list 2 is also sorted
# Time = O(m*n) or O(n*m)
# AUX = O(1)
def merge(arr1, arr2):
    x = arr1; y = arr2
    end = len(arr1)
    i = 0
    while(i < end):                 # O(m) or O(n)
        if(x[i] > y[0]):
            swap(x,y,i,0)
            insert(y,0)             # O(n) or O(m) number of shifts
        i+=1
 
# O(n):
def insert(y, i):
    orig = y[i]
    i+=1
    while (i<len(y) and y[i]<orig):
        y[i-1] = y[i]
        i+=1
    y[i-1] = orig
 
def swap(x,y,i,j):
    temp = x[i]
    x[i] = y[j]
    y[j] = temp
 
def test():
    c1 = [2, 3, 8, 13]
    c2 = [1, 5, 9, 10, 15, 20 ]
    for _ in range(2):
        merge(c1,c2)
        print(c1,c2)
        c1, c2 = c2, c1
 
test()

C#

using System;
 
public class GFG {
 
    static void merge(int []arr1, int []arr2, int n, int m) {
        // two pointer to iterate
        int i = 0;
        int j = 0;
        while (i < n && j < m) {
 
            // if arr1[i] <= arr2[j] then both array is already
            // sorted
            if (arr1[i] <= arr2[j]) {
                i++;
            } else if (arr1[i] > arr2[j]) {
 
                // if arr1[i]>arr2[j] then first we swap both
                // element so that arr1[i] become smaller means
                // arr1[] become sorted then we check that
                // arr2[j] is smaller than all other element in
                // right side of arr2[j] if arr2[] is not sorted
                // then we linearly do sorting
                // means while adjacent element are less than
                // new arr2[j] we do sorting like by changing
                // position of element by shifting one position
                // toward left
                int t = arr1[i];
                arr1[i] = arr2[j];
                arr2[j] = t;
                i++;
                if (j < m - 1 && arr2[j + 1] < arr2[j]) {
                    int temp = arr2[j];
                    int tempj = j + 1;
                    while (tempj < m && arr2[tempj] < temp && tempj < m) {
                        arr2[tempj - 1] = arr2[tempj];
                        tempj++;
                    }
                    arr2[tempj - 1] = temp;
                }
            }
        }
    }
 
    public static void Main(String[] args) {
 
        int []ar1 = { 1, 5, 9, 10, 15, 20 };
        int []ar2 = { 2, 3, 8, 13 };
        int m = ar1.Length;
        int n = ar2.Length;
        merge(ar1, ar2, m, n);
 
        Console.Write("After Merging \nFirst Array: ");
        for (int i = 0; i < m; i++)
            Console.Write(ar1[i] + " ");
        Console.Write("\nSecond Array: ");
        for (int i = 0; i < n; i++)
            Console.Write(ar2[i] + " ");
    }
}
 
// This code is contributed by gauravrajput1

Javascript

<script>
    function merge(arr1 , arr2 , n , m) {
        // two pointer to iterate
        var i = 0;
        var j = 0;
        while (i < n && j < m) {
 
            // if arr1[i] <= arr2[j] then both array is already
            // sorted
            if (arr1[i] <= arr2[j]) {
                i++;
            } else if (arr1[i] > arr2[j]) {
 
                // if arr1[i]>arr2[j] then first we swap both
                // element so that arr1[i] become smaller means
                // arr1 become sorted then we check that
                // arr2[j] is smaller than all other element in
                // right side of arr2[j] if arr2 is not sorted
                // then we linearly do sorting
                // means while adjacent element are less than
                // new arr2[j] we do sorting like by changing
                // position of element by shifting one position
                // toward left
                var t = arr1[i];
                arr1[i] = arr2[j];
                arr2[j] = t;
                i++;
                if (j < m - 1 && arr2[j + 1] < arr2[j]) {
                    var temp = arr2[j];
                    var tempj = j + 1;
                    while (tempj < m && arr2[tempj] < temp && tempj < m) {
                        arr2[tempj - 1] = arr2[tempj];
                        tempj++;
                    }
                    arr2[tempj - 1] = temp;
                }
            }
        }
    }
 
     
 
        var ar1 = [ 1, 5, 9, 10, 15, 20 ];
        var ar2 = [ 2, 3, 8, 13 ];
        var m = ar1.length;
        var n = ar2.length;
        merge(ar1, ar2, m, n);
 
        document.write("After Merging <br/>First Array: <br/>");
        for (i = 0; i < m; i++)
            document.write(ar1[i] + " ");
        document.write("<br/>Second Array: <br/>");
        for (i = 0; i < n; i++)
            document.write(ar2[i] + " ");
 
// This code contributed by gauravrajput1
</script>

Output

After Merging 
First Array: 1 2 3 5 8 9 
Second Array: 10 13 15 20

Time Complexity: O(m*n) list 1 traversal and list 2 insertions
Auxiliary Space: O(1)
If m == n: Time = O(n^2) insertion sort complexity

Method-6 [Using Euclidean Division Lemma]

Approach:
Just merge the two arrays as we do in merge sort, while simultaneously using Euclidean Division Lemma, i.e. (((Operation on array) % x) * x). And at least after merging divide both the arrays with x. Where x needs to be a number greater than all elements of array. Here in this case x, (according to the constraints) can be 10e7 + 1.

C++

// C++ program to merge two sorted arrays without using extra space
#include <bits/stdc++.h>
 
using namespace std;
 
void merge(int arr1[], int arr2[], int n, int m)
{
    // three pointers to iterate
    int i = 0, j = 0, k = 0;
    // for euclid's division lemma
    int x = 10e7 + 1;
    // in this loop we are rearranging the elements of arr1
    while (i < n && (j < n && k < m)) {
        // if both arr1 and arr2 elements are modified
        if (arr1[j] >= x && arr2[k] >= x) {
            if (arr1[j] % x <= arr2[k] % x) {
                arr1[i] += (arr1[j++] % x) * x;
            }
            else {
                arr1[i] += (arr2[k++] % x) * x;
            }
        }
        // if only arr1 elements are modified
        else if (arr1[j] >= x) {
            if (arr1[j] % x <= arr2[k]) {
                arr1[i] += (arr1[j++] % x) * x;
            }
            else {
                arr1[i] += (arr2[k++] % x) * x;
            }
        }
        // if only arr2 elements are modified
        else if (arr2[k] >= x) {
            if (arr1[j] <= arr2[k] % x) {
                arr1[i] += (arr1[j++] % x) * x;
            }
            else {
                arr1[i] += (arr2[k++] % x) * x;
            }
        }
        // if none elements are modified
        else {
            if (arr1[j] <= arr2[k]) {
                arr1[i] += (arr1[j++] % x) * x;
            }
            else {
                arr1[i] += (arr2[k++] % x) * x;
            }
        }
        i++;
    }
    // we can copy the elements directly as the other array
    // is exchausted
    while (j < n && i < n) {
        arr1[i++] += (arr1[j++] % x) * x;
    }
    while (k < m && i < n) {
        arr1[i++] += (arr2[k++] % x) * x;
    }
    // we need to reset i
    i = 0;
    // in this loop we are rearranging the elements of arr2
    while (i < m && (j < n && k < m)) {
        // if both arr1 and arr2 elements are modified
        if (arr1[j] >= x && arr2[k] >= x) {
            if (arr1[j] % x <= arr2[k] % x) {
                arr2[i] += (arr1[j++] % x) * x;
            }
            else {
                arr2[i] += (arr2[k++] % x) * x;
            }
        }
        // if only arr1 elements are modified
        else if (arr1[j] >= x) {
            if (arr1[j] % x <= arr2[k]) {
                arr2[i] += (arr1[j++] % x) * x;
            }
            else {
                arr2[i] += (arr2[k++] % x) * x;
            }
        }
        // if only arr2 elements are modified
        else if (arr2[k] >= x) {
            if (arr1[j] <= arr2[k] % x) {
                arr2[i] += (arr1[j++] % x) * x;
            }
            else {
                arr2[i] += (arr2[k++] % x) * x;
            }
        }
        else {
            // if none elements are modified
            if (arr1[j] <= arr2[k]) {
                arr2[i] += (arr1[j++] % x) * x;
            }
            else {
                arr2[i] += (arr2[k++] % x) * x;
            }
        }
        i++;
    }
    // we can copy the elements directly as the other array
    // is exhausted
    while (j < n && i < m) {
        arr2[i++] += (arr1[j++] % x) * x;
    }
    while (k < m && i < m) {
        arr2[i++] += (arr2[k++] % x) * x;
    }
    // we need to reset i
    i = 0;
    // we need to divide the whole arr1 by x
    while (i < n) {
        arr1[i++] /= x;
    }
    // we need to reset i
    i = 0;
    // we need to divide the whole arr2 by x
    while (i < m) {
        arr2[i++] /= x;
    }
}
 
int main()
{
 
    int ar1[] = { 1, 5, 9, 10, 15, 20 };
    int ar2[] = { 2, 3, 8, 13 };
    int m = sizeof(ar1) / sizeof(ar1[0]);
    int n = sizeof(ar2) / sizeof(ar2[0]);
    merge(ar1, ar2, m, n);
 
    cout << "After Merging \nFirst Array: ";
    for (int i = 0; i < m; i++)
        cout << ar1[i] << " ";
    cout << "\nSecond Array: ";
    for (int i = 0; i < n; i++)
        cout << ar2[i] << " ";
    return 0;
}
// This code is contributed by @ancientmoon8 (Mayank Kashyap)

Java

import java.util.*;
class GFG{
  
static void merge(int arr1[], int arr2[], int n, int m)
{
    // three pointers to iterate
    int i = 0, j = 0, k = 0;
   
    // for euclid's division lemma
    int x=10000000+7;
   
    // in this loop we are rearranging the elements of arr1
    while (i < n && (j < n && k < m))
    {
       
        // if both arr1 and arr2 elements are modified
        if (arr1[j] >= x && arr2[k] >= x) {
            if (arr1[j] % x <= arr2[k] % x) {
                arr1[i] += (arr1[j++] % x) * x;
            }
            else {
                arr1[i] += (arr2[k++] % x) * x;
            }
        }
       
        // if only arr1 elements are modified
        else if (arr1[j] >= x) {
            if (arr1[j] % x <= arr2[k]) {
                arr1[i] += (arr1[j++] % x) * x;
            }
            else {
                arr1[i] += (arr2[k++] % x) * x;
            }
        }
       
        // if only arr2 elements are modified
        else if (arr2[k] >= x) {
            if (arr1[j] <= arr2[k] % x) {
                arr1[i] += (arr1[j++] % x) * x;
            }
            else {
                arr1[i] += (arr2[k++] % x) * x;
            }
        }
       
        // if none elements are modified
        else {
            if (arr1[j] <= arr2[k]) {
                arr1[i] += (arr1[j++] % x) * x;
            }
            else {
                arr1[i] += (arr2[k++] % x) * x;
            }
        }
        i++;
    }
   
    // we can copy the elements directly as the other array
    // is exchausted
    while (j < n && i < n) {
        arr1[i++] += (arr1[j++] % x) * x;
    }
    while (k < m && i < n) {
        arr1[i++] += (arr2[k++] % x) * x;
    }
   
    // we need to reset i
    i = 0;
   
    // in this loop we are rearranging the elements of arr2
    while (i < m && (j < n && k < m))
    {
       
        // if both arr1 and arr2 elements are modified
        if (arr1[j] >= x && arr2[k] >= x) {
            if (arr1[j] % x <= arr2[k] % x) {
                arr2[i] += (arr1[j++] % x) * x;
            }
            else {
                arr2[i] += (arr2[k++] % x) * x;
            }
        }
       
        // if only arr1 elements are modified
        else if (arr1[j] >= x) {
            if (arr1[j] % x <= arr2[k]) {
                arr2[i] += (arr1[j++] % x) * x;
            }
            else {
                arr2[i] += (arr2[k++] % x) * x;
            }
        }
       
        // if only arr2 elements are modified
        else if (arr2[k] >= x) {
            if (arr1[j] <= arr2[k] % x) {
                arr2[i] += (arr1[j++] % x) * x;
            }
            else {
                arr2[i] += (arr2[k++] % x) * x;
            }
        }
        else
        {
           
            // if none elements are modified
            if (arr1[j] <= arr2[k]) {
                arr2[i] += (arr1[j++] % x) * x;
            }
            else {
                arr2[i] += (arr2[k++] % x) * x;
            }
        }
        i++;
    }
   
    // we can copy the elements directly as the other array
    // is exhausted
    while (j < n && i < m) {
        arr2[i++] += (arr1[j++] % x) * x;
    }
    while (k < m && i < m) {
        arr2[i++] += (arr2[k++] % x) * x;
    }
   
    // we need to reset i
    i = 0;
   
    // we need to divide the whole arr1 by x
    while (i < n) {
        arr1[i++] /= x;
    }
   
    // we need to reset i
    i = 0;
   
    // we need to divide the whole arr2 by x
    while (i < m) {
        arr2[i++] /= x;
    }
}
  
public static void main(String[] args)
{
  
    int ar1[] = { 1, 5, 9, 10, 15, 20 };
    int ar2[] = { 2, 3, 8, 13 };
    int m = ar1.length;
    int n =ar2.length;
    merge(ar1, ar2, m, n);
  
    System.out.print("After Merging \nFirst Array: ");
    for (int i = 0; i < m; i++)
        System.out.print(ar1[i]+ " ");
    System.out.print("\nSecond Array: ");
    for (int i = 0; i < n; i++)
        System.out.print(ar2[i]+ " ");
}
}
  
// This code is contributed by Aarti_Rathi

Python3

# Python program to merge two sorted arrays without using extra space
 
 
def merge(arr1, arr2, n, m):
    # three pointers to iterate
    i = 0
    j = 0
    k = 0
    # for euclid's division lemma
    x = 10e7 + 1
    # in this loop we are rearranging the elements of arr1
    while i < n and (j < n and k < m):
        # if both arr1 and arr2 elements are modified
        if arr1[j] >= x and arr2[k] >= x:
            if arr1[j] % x <= arr2[k] % x:
                arr1[i] += (arr1[j] % x) * x
                j += 1
            else:
                arr1[i] += (arr2[k] % x) * x
                k += 1
        # if only arr1 elements are modified
        elif arr1[j] >= x:
            if arr1[j] % x <= arr2[k]:
                arr1[i] += (arr1[j] % x) * x
                j += 1
            else:
                arr1[i] += (arr2[k] % x) * x
                k += 1
        # if only arr2 elements are modified
        elif arr2[k] >= x:
            if arr1[j] <= arr2[k] % x:
                arr1[i] += (arr1[j] % x) * x
                j += 1
            else:
                arr1[i] += (arr2[k] % x) * x
                k += 1
        # if none elements are modified
        else:
            if arr1[j] <= arr2[k]:
                arr1[i] += (arr1[j] % x) * x
                j += 1
            else:
                arr1[i] += (arr2[k] % x) * x
                k += 1
        i += 1
 
    #  we can copy the elements directly as the other array
    #  is exchausted
    while j < n and i < n:
        arr1[i] += (arr1[j] % x) * x
        i += 1
        j += 1
    while k < m and i < n:
        arr1[i] += (arr2[k] % x) * x
        i += 1
        k += 1
    #  we need to reset i
    i = 0
 
    # in this loop we are rearranging the elements of arr2
    while i < m and (j < n and k < m):
        # if both arr1 and arr2 elements are modified
        if arr1[j] >= x and arr2[k] >= x:
            if arr1[j] % x <= arr2[k] % x:
                arr2[i] += (arr1[j] % x) * x
                j += 1
 
            else:
                arr2[i] += (arr2[k] % x) * x
                k += 1
 
        # if only arr1 elements are modified
        elif arr1[j] >= x:
            if arr1[j] % x <= arr2[k]:
                arr2[i] += (arr1[j] % x) * x
                j += 1
 
            else:
                arr2[i] += (arr2[k] % x) * x
                k += 1
 
        # if only arr2 elements are modified
        elif arr2[k] >= x:
            if arr1[j] <= arr2[k] % x:
                arr2[i] += (arr1[j] % x) * x
                j += 1
 
            else:
                arr2[i] += (arr2[k] % x) * x
                k += 1
 
        else:
            # if none elements are modified
            if arr1[j] <= arr2[k]:
                arr2[i] += (arr1[j] % x) * x
                j += 1
 
            else:
                arr2[i] += (arr2[k] % x) * x
                k += 1
 
        i += 1
    # we can copy the elements directly as the other array
    # is exhausted
    while j < n and i < m:
        arr2[i] += (arr1[j] % x) * x
        i += 1
        j += 1
 
    while k < m and i < m:
        arr2[i] += (arr2[k] % x) * x
        i += 1
        k += 1
 
    # we need to reset i
    i = 0
    # we need to divide the whole arr1 by x
    while i < n:
        arr1[i] /= x
        i += 1
 
    # we need to reset i
    i = 0
    # we need to divide the whole arr2 by x
    while i < m:
        arr2[i] /= x
        i += 1
 
# Driver program
 
 
ar1 = [1, 5, 9, 10, 15, 20]
ar2 = [2, 3, 8, 13]
m = len(ar1)
n = len(ar2)
 
merge(ar1, ar2, m, n)
 
print("After Merging \nFirst Array:", end=" ")
for i in range(m):
    print(int(ar1[i]), end=" ")
print("\nSecond Array:", end=" ")
for i in range(n):
    print(int(ar2[i]), end=" ")
     
# This code is contributed by Tapesh(tapeshdua420)

C#

using System;
 
public class GFG {
 
  static void merge(int []arr1, int []arr2, int n, int m)
  {
 
    // three pointers to iterate
    int i = 0, j = 0, k = 0;
 
    // for euclid's division lemma
    int x = 10000000 + 1;
 
    // in this loop we are rearranging the elements of arr1
    while (i < n && (j < n && k < m))
    {
 
      // if both arr1 and arr2 elements are modified
      if (arr1[j] >= x && arr2[k] >= x) {
        if (arr1[j] % x <= arr2[k] % x) {
          arr1[i] += (arr1[j++] % x) * x;
        }
        else {
          arr1[i] += (arr2[k++] % x) * x;
        }
      }
 
      // if only arr1 elements are modified
      else if (arr1[j] >= x) {
        if (arr1[j] % x <= arr2[k]) {
          arr1[i] += (arr1[j++] % x) * x;
        }
        else {
          arr1[i] += (arr2[k++] % x) * x;
        }
      }
 
      // if only arr2 elements are modified
      else if (arr2[k] >= x) {
        if (arr1[j] <= arr2[k] % x) {
          arr1[i] += (arr1[j++] % x) * x;
        }
        else {
          arr1[i] += (arr2[k++] % x) * x;
        }
      }
 
      // if none elements are modified
      else {
        if (arr1[j] <= arr2[k]) {
          arr1[i] += (arr1[j++] % x) * x;
        }
        else {
          arr1[i] += (arr2[k++] % x) * x;
        }
      }
      i++;
    }
 
    // we can copy the elements directly as the other array
    // is exchausted
    while (j < n && i < n) {
      arr1[i++] += (arr1[j++] % x) * x;
    }
    while (k < m && i < n) {
      arr1[i++] += (arr2[k++] % x) * x;
    }
 
    // we need to reset i
    i = 0;
 
    // in this loop we are rearranging the elements of arr2
    while (i < m && (j < n && k < m))
    {
 
      // if both arr1 and arr2 elements are modified
      if (arr1[j] >= x && arr2[k] >= x) {
        if (arr1[j] % x <= arr2[k] % x) {
          arr2[i] += (arr1[j++] % x) * x;
        }
        else {
          arr2[i] += (arr2[k++] % x) * x;
        }
      }
 
      // if only arr1 elements are modified
      else if (arr1[j] >= x) {
        if (arr1[j] % x <= arr2[k]) {
          arr2[i] += (arr1[j++] % x) * x;
        }
        else {
          arr2[i] += (arr2[k++] % x) * x;
        }
      }
 
      // if only arr2 elements are modified
      else if (arr2[k] >= x) {
        if (arr1[j] <= arr2[k] % x) {
          arr2[i] += (arr1[j++] % x) * x;
        }
        else {
          arr2[i] += (arr2[k++] % x) * x;
        }
      }
      else
      {
 
        // if none elements are modified
        if (arr1[j] <= arr2[k]) {
          arr2[i] += (arr1[j++] % x) * x;
        }
        else {
          arr2[i] += (arr2[k++] % x) * x;
        }
      }
      i++;
    }
 
    // we can copy the elements directly as the other array
    // is exhausted
    while (j < n && i < m) {
      arr2[i++] += (arr1[j++] % x) * x;
    }
    while (k < m && i < m) {
      arr2[i++] += (arr2[k++] % x) * x;
    }
 
    // we need to reset i
    i = 0;
 
    // we need to divide the whole arr1 by x
    while (i < n) {
      arr1[i++] /= x;
    }
 
    // we need to reset i
    i = 0;
 
    // we need to divide the whole arr2 by x
    while (i < m) {
      arr2[i++] /= x;
    }
  }
 
  public static void Main(String[] args) {
 
    int []ar1 = { 1, 5, 9, 10, 15, 20 };
    int []ar2 = { 2, 3, 8, 13 };
    int m = ar1.Length;
    int n = ar2.Length;
    merge(ar1, ar2, m, n);
 
    Console.Write("After Merging \nFirst Array: ");
    for (int i = 0; i < m; i++)
      Console.Write(ar1[i] + " ");
    Console.Write("\nSecond Array: ");
    for (int i = 0; i < n; i++)
      Console.Write(ar2[i] + " ");
  }
}
 
// This code is contributed by Aarti_Rathi

Javascript

// JavaScript program to merge two sorted arrays without using extra space
static merge(arr1, arr2, n, m)
{
    // three pointers to iterate
    var i = 0;
    var j = 0;
    var k = 0;
     
    // for euclid's division lemma
    var x = 10000000 + 7;
     
    // in this loop we are rearranging the elements of arr1
    while (i < n && (j < n && k < m))
    {
     
        // if both arr1 and arr2 elements are modified
        if (arr1[j] >= x && arr2[k] >= x)
        {
            if (arr1[j] % x <= arr2[k] % x)
            {
                arr1[i] += (arr1[j++] % x) * x;
            }
            else
            {
                arr1[i] += (arr2[k++] % x) * x;
            }
        }
        else if (arr1[j] >= x)
        {
            if (arr1[j] % x <= arr2[k])
            {
                arr1[i] += (arr1[j++] % x) * x;
            }
            else
            {
                arr1[i] += (arr2[k++] % x) * x;
            }
        }
        else if (arr2[k] >= x)
        {
            if (arr1[j] <= arr2[k] % x)
            {
                arr1[i] += (arr1[j++] % x) * x;
            }
            else
            {
                arr1[i] += (arr2[k++] % x) * x;
            }
        }
        else
        {
            if (arr1[j] <= arr2[k])
            {
                arr1[i] += (arr1[j++] % x) * x;
            }
            else
            {
                arr1[i] += (arr2[k++] % x) * x;
            }
        }
        i++;
    }
     
    // we can copy the elements directly as the other array
    // is exchausted
    while (j < n && i < n)
    {
        arr1[i++] += (arr1[j++] % x) * x;
    }
    while (k < m && i < n)
    {
        arr1[i++] += (arr2[k++] % x) * x;
    }
     
    // we need to reset i
    i = 0;
     
    // in this loop we are rearranging the elements of arr2
    while (i < m && (j < n && k < m))
    {
     
        // if both arr1 and arr2 elements are modified
        if (arr1[j] >= x && arr2[k] >= x)
        {
            if (arr1[j] % x <= arr2[k] % x)
            {
                arr2[i] += (arr1[j++] % x) * x;
            }
            else
            {
                arr2[i] += (arr2[k++] % x) * x;
            }
        }
        else if (arr1[j] >= x)
        {
            if (arr1[j] % x <= arr2[k])
            {
                arr2[i] += (arr1[j++] % x) * x;
            }
            else
            {
                arr2[i] += (arr2[k++] % x) * x;
            }
        }
        else if (arr2[k] >= x)
        {
            if (arr1[j] <= arr2[k] % x)
            {
                arr2[i] += (arr1[j++] % x) * x;
            }
            else
            {
                arr2[i] += (arr2[k++] % x) * x;
            }
        }
        else
        {
         
            // if none elements are modified
            if (arr1[j] <= arr2[k])
            {
                arr2[i] += (arr1[j++] % x) * x;
            }
            else
            {
                arr2[i] += (arr2[k++] % x) * x;
            }
        }
        i++;
    }
     
    // we can copy the elements directly as the other array
    // is exhausted
    while (j < n && i < m)
    {
        arr2[i++] += (arr1[j++] % x) * x;
    }
    while (k < m && i < m)
    {
        arr2[i++] += (arr2[k++] % x) * x;
    }
     
    // we need to reset i
    i = 0;
     
    // we need to divide the whole arr1 by x
    while (i < n)
    {
        arr1[i++] /= x;
    }
     
    // we need to reset i
    i = 0;
     
    // we need to divide the whole arr2 by x
    while (i < m)
    {
        arr2[i++] /= x;
    }
}
 
var ar1 = [1, 5, 9, 10, 15, 20];
var ar2 = [2, 3, 8, 13];
var m = ar1.length;
var n = ar2.length;
GFG.merge(ar1, ar2, m, n);
console.log("After Merging \nFirst Array: ");
for (var i=0; i < m; i++)
{
    console.log(parseInt(ar1[i]) + " ");
}
console.log("\nSecond Array: ");
for (var i=0; i < n; i++)
{
    console.log(parseInt(ar2[i]) + " ");
}
 
// This code is contributed by Aarti_Rathi

Output

After Merging 
First Array: 1 2 3 5 8 9 
Second Array: 10 13 15 20

Time Complexity: O(m + n)
Auxiliary Space: O(1), since no extra space has been taken.

Related Articles :
Merge two sorted arrays
Merge k sorted arrays | Set 1
Thanks to Shubham Chauhan for suggesting 1st solution and Himanshu Kaushik for the 2nd solution. Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above

My Personal Notes