Mensuration 2D | Set 2

Question 1: A square of perimeter 88cm and a circle of perimeter 88cm given. Which figure has larger area and by how much? 
Solution: Perimeter of square =88 cm 
4 x side = 88, side = 22 
Area of square = (22)² = 484 cm²
Circumference of circle =88cm 
2π(radius) = 88 
radius = 44*7/22 = 14 
Area of circle = π (radius)²
=22/7 * 14 * 14 = 616 cm²
Area of circle – Area of square = 616 – 484 = 132 cm²
Hence, circle has larger area than square by 132 cm²
Question 2: The areas of a square and a rectangle are equal. The length of the rectangle is greater than the length of any side of the square by 4cm and the breadth is less by 3cm. Find the perimeter of the rectangle. 
Solution: Let the side of square is a, then 
length of rectangle is a+4 
breadth of rectangle is a-3 
Acc. to question – 
Area of square = Area of rectangle 
a² = (a+4)(a-3) 
a² = a² + 4a – 3a – 12 
a = 12 
Perimeter of rectangle = 2(l+b) 
=2(16 + 9) =50 cm 
Hence, perimeter of rectangle is 50 cm
Question 3: A wire is bent in the shape of square of area 324cm². If the same wire is bent in the form of a semicircle, the radius of the semicircle is 
Solution: Let the side of the square is a. 
a² = 324, a = 18 
Perimeter of the square = 4 x 18 = 72 cm 
Let radius of the semicircle is r. 
Perimeter of the semicircle = 2r + πr 
Acc to question 
2r + πr = 72 
r(2 + 22/7)= 72 
r = 72 * 7 /36 
r =14 cm 
Hence radius of the semicircle is 14cm
Question 4: A kite is in the shape of a square with a diagonal 24cm attached to a triangle of the base 4cm and height 6cm. How much paper has been used to make it? 
Solution: Area of square = 1/2(diagonal)²
=1/2 * (24)²
=288 cm²
Area of triangle = 1/2 * base * height 
= 1/2 * 4 * 6 = 12 cm²
Total area = 288 + 12 = 300 cm²
Question 5: The area of a sector of a circle of radius 10cm, formed by an arc of length 7cm is 
Solution: Radius of circle(r)= 10cm 
Length of arc(l)=7cm 
Area of sector = 1/2 lr 
= 1/2 * 7 * 10 
= 35 cm²

Question 6: Three circles of radius 7cm each are placed in such a way that each touches the other two.The area of portion enclosed by the circles is(√3 = 1.732) 
Solution :Diagram for the solution 

Radius of circle = 7cm 
Sides of the triangle AB=BC=CA = 14cm 
and, angle of equilateral triangle is 60^o. 
Three arcs combined to form area 1/2(circle). 
Area enclosed = Area of triangle – 1/2*(Area of a circle) 
= √3/4 (14)² – 1/2[22/7*(7)²] 
= 1.732×49 – 77 
= 84.868 – 77 
= 7.868 cm²
Question 7: From a point in the interior of an equilateral triangle, the perpendicular distance of the sides are 2√3, 3√3 and 4√3. Find the perimeter of the triangle. 
Solution :

Let O is the intersection point of all the perpendiculars and Let x is the side of equilateral triangle. 
OP=2√3, OR= 3√3 and OQ=4√3 
Area of ∆ABC = ar∆ABO + ar∆ACO + ar∆BOC 
√3/4 x² = 1/2*x*2√3 + 1/2*x*3√3 + 1/2*x*4√3 
√3x² = 4√3x + 6√3x + 8√3x 
√3x = 18√3 
x = 18 cm 
Hence, Perimeter of the equilateral triangle = 3x = 3*18 = 54 cm 
Question 8: Find the diameter of a wheel that makes 226 revolutions to go 4520 meter. 
Solution :Total distance = 4520 meter 
No of revolutions = 226 
Distance covered in 1 revolution = 4520 / 226 = 20 m 
We know that 
2 π r = 20 m 
2r = 20 * 7/22 
Diameter(2r) = 70/11 m 
Question 9: The circum-radius of an equilateral triangle is 10cm. The in-radius of the triangle is 
Solution: 

Circum-radius(OA) of equilateral triangle is = (side)/√3 
10 = side/√3 
side = 10√3 
In-radius(OB) of the equilateral triangle = side/2√3 
= 10√3/2√3 
= 5 
Hence, In-radius of equilateral triangle is 5 cm. 
Question 10: The base and altitude of a right angled triangle are 7cm and 24cm respectively. The perpendicular distance of its hypotenuse from the opposite vertex is 
Solution :
First find the length of hypotenuse (H) 
(H)² = (Base)² + (Altitude)²
(H)² = (7)² + (24)²
(H)² = 49 + 576 
H = √625 = 25cm 
Perpendicular distance of its hypotenuse = (base x altitude) /H 
= (7 x 24) / 25 
= 168/25 cm
Question 11: The perimeter of a rhombus is 80 cm, If one of its diagonals is 24 cm long, what is the area of rhombus? 
Solution :

NOTE: Diagonals of rhombus bisect each other at 90^o angle. 
In ∆ AOB 
Perimeter = 4 x side 
side = 80/4 = 20 cm 
OB= √ (20²– 12²) 
= √(400 – 144) 
= √256 = 16 cm 
So, diagonal BD = 2 x 16 = 32 cm 
Area of rhombus = 1/2 x d₁ x d₂
= 1/2 x 24 x 32 
= 384 cm²
Question 12: The ratio of the length of parallel sides of a trapezium is 3:2. The shortest distance between them is 30 cm. If the area of the trapezium is 900 cm², the sum of the length of the parallel sides is 
Solution :Let the parallel sides be 3x and 2x. 
Area of trapezium = 1/2(sum of the parallel sides) * distance between parallel sides 
1/2 (3x + 2x)*30 = 900 
5x = 60 
x = 12 
Sum of length of parallel sides = 5*12 = 60 cm 
Question 13: Two sides of a parallelogram 30cm and 14cm long. The length of one of the diagonals is 40 cm. The area of a parallelogram is – 
Solution : Using heron’s formula we find the area of one half of parallelogram. 
S = (30 + 14 + 40) /2 = 42 
Area of half triangle= 

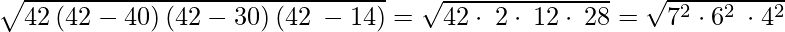
= 7*6*4 
= 168 cm²
Area of parallelogram = 2 x area of triangle 
= 2 x 168 
= 336 cm²
Question 14: The sides of a triangle are in the ratio 1/2 : 1/3 : 1/6 . If the perimeter of the triangles in 60cm, the length of the largest side is: 
Solution : Acc. to question 
Ratio = 1/2 : 1/3 : 1/6 
Take LCM of the denominator as 6 and multiply each of them 
New ratio = 3 : 2 : 1 
Now, 
3x + 2x + x = 60 
6x =60 
x = 10 cm 
Length of the largest side is 3*10 = 30 cm