Memory representation of Binomial Heap

Prerequisites: Binomial Heap

Binomial trees are multi-way trees typically stored in the left-child, right-sibling representation, and each node stores its degree. Binomial heaps are collection of binomial trees stored in ascending order of size. The root list in the heap is a linked list of roots of the Binomial heap. The degree of the nodes of the roots increase as on traversing the root list.

The number of binomial trees in a binomial heap can be found with the binary value of the number of nodes in the binomial heap. This article focuses on memory representation of binomial heaps.

Binomial Heap Node:

• Fields in each node:

  Each node in a binomial heap has 5 fields :

  1. Pointer to parent
  2. Key
  3. Degree
  4. Pointer to child (leftmost child)
  5. Pointer to sibling which is immediately to its right

  

• Pointers in each node:

  Each node has the following pointers:

  1. A parent pointer pointing to the immediate parent of the node
  2. A left pointer pointing to the first child of the node
  3. A right pointer pointing to the next sibling of the node.

Types of nodes and their representations:

• Single node in the Heap:

  

• Parent – Child relationship between nodes:

  

• Sibling relationship between nodes:

  

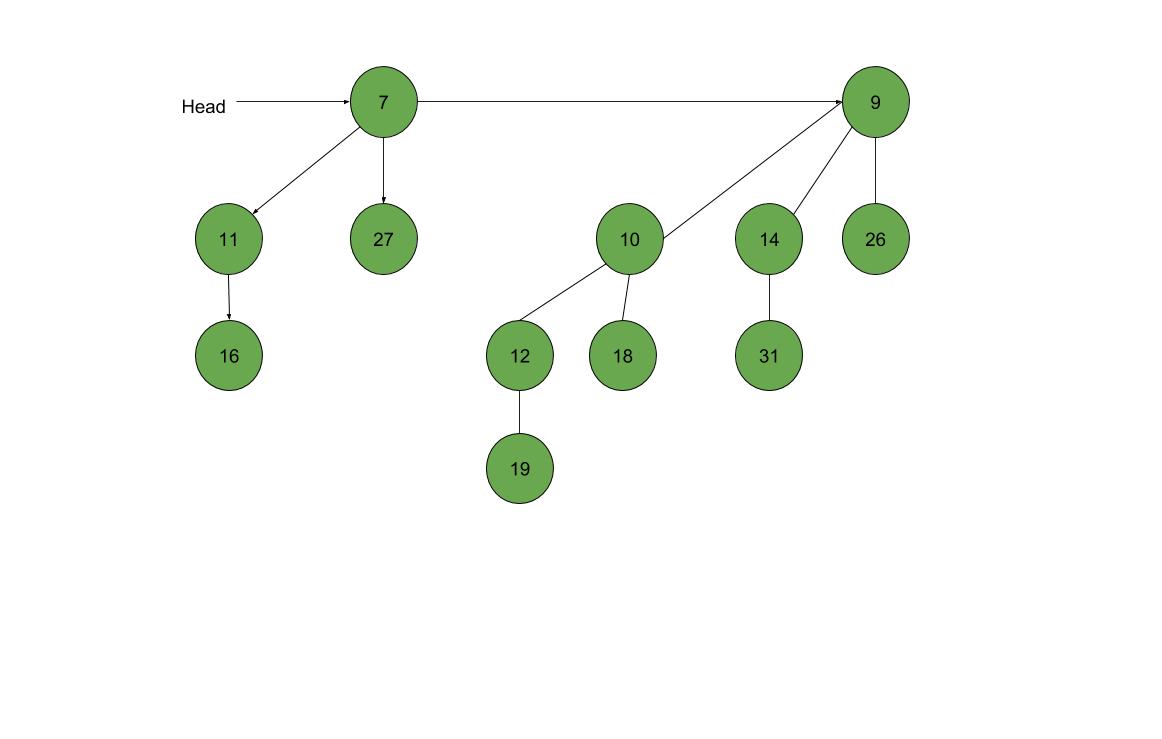
Representation of Full binomial heap:

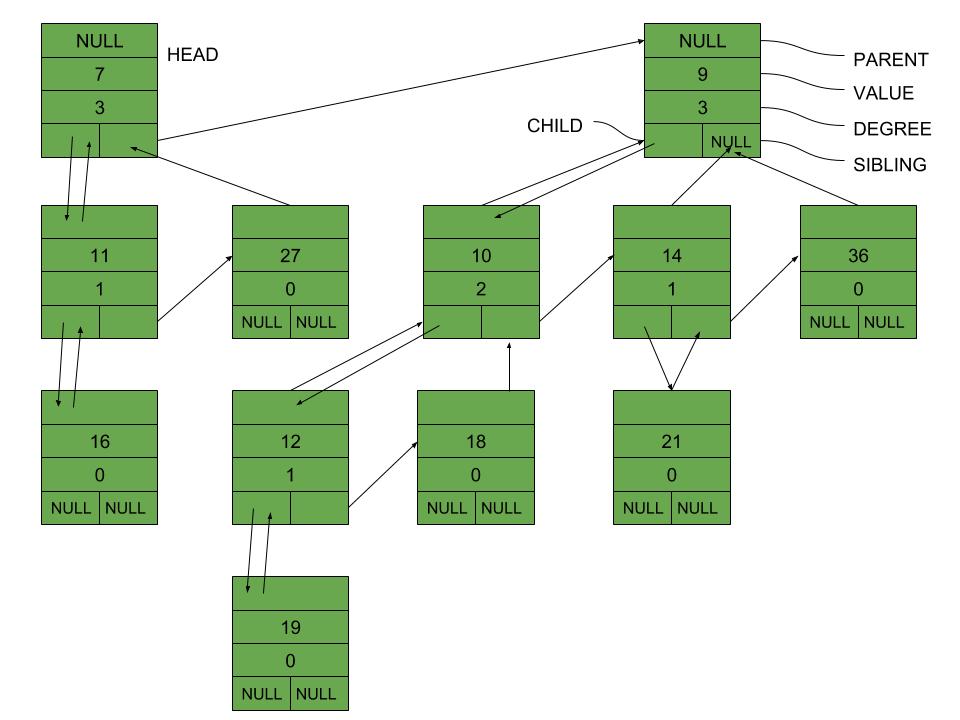
The memory representation of each node of the Binomial heap given above can be illustrated using the following diagram: