Measures of Distance in Data Mining
Last Updated :
03 Feb, 2020
Clustering consists of grouping certain objects that are similar to each other, it can be used to decide if two items are similar or dissimilar in their properties.
In a
Data Mining sense, the similarity measure is a distance with dimensions describing object features. That means if the distance among two data points is
small then there is a
high degree of similarity among the objects and vice versa. The similarity is
subjective and depends heavily on the context and application. For example, similarity among vegetables can be determined from their taste, size, colour etc.
Most clustering approaches use distance measures to assess the similarities or differences between a pair of objects, the most popular distance measures used are:
1. Euclidean Distance:
Euclidean distance is considered the traditional metric for problems with geometry. It can be simply explained as the
ordinary distance between two points. It is one of the most used algorithms in the cluster analysis. One of the algorithms that use this formula would be
K-mean. Mathematically it computes the
root of squared differences between the coordinates between two objects.
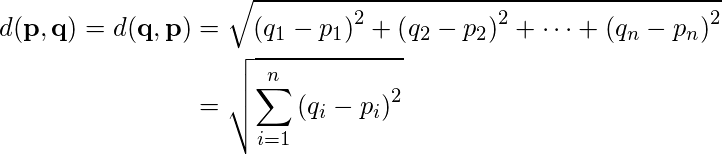
 Figure – Euclidean Distance
2. Manhattan Distance:
Figure – Euclidean Distance
2. Manhattan Distance:
This determines the absolute difference among the pair of the coordinates.
Suppose we have two points P and Q to determine the distance between these points we simply have to calculate the perpendicular distance of the points from X-Axis and Y-Axis.
In a plane with P at coordinate (x1, y1) and Q at (x2, y2).
Manhattan distance between P and Q = |x1 – x2| + |y1 – y2|

Here the total distance of the
Red line gives the Manhattan distance between both the points.
3. Jaccard Index:
The Jaccard distance measures the similarity of the two data set items as the
intersection of those items divided by the
union of the data items.
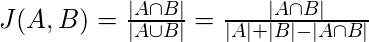
 Figure – Jaccard Index
4. Minkowski distance:
Figure – Jaccard Index
4. Minkowski distance:
It is the
generalized form of the Euclidean and Manhattan Distance Measure. In an
N-dimensional space, a point is represented as,
(x1, x2, ..., xN)
Consider two points P1 and P2:
P1: (X1, X2, ..., XN)
P2: (Y1, Y2, ..., YN)
Then, the Minkowski distance between P1 and P2 is given as:
![Rendered by QuickLaTeX.com \sqrt[p]{(x 1-y 1)^{p}+(x 2-y 2)^{p}+\ldots+(x N-y N)^{p}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4b4c94cc46facdb2183fb68d468dfe47_l3.png)
- When p = 2, Minkowski distance is same as the Euclidean distance.
- When p = 1, Minkowski distance is same as the Manhattan distance.
5. Cosine Index:
Cosine distance measure for clustering determines the
cosine of the angle between two vectors given by the following formula.
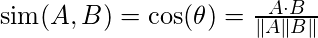
Here (
theta) gives the angle between two vectors and A, B are n-dimensional vectors.
 Figure – Cosine Distance
Figure – Cosine Distance
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...