Mean Free Path – Definition, Formula, Derivation, Examples
Last Updated :
10 Dec, 2021
The kinetic theory was introduced to explain the structure and composition of molecules with respect to submicroscopic particles. The theory talks about the increase in pressure due to the constant movement and collision of the submicroscopic particles. It also discusses other properties of a gas such as a temperature, pressure, volume, viscosity, diffusion, thermal conductivity, etc. The theory develops a relationship between the microscopic particles and the macroscopic properties. The molecule of gas is always in constant motion and keeps colliding with each other and to the walls of the container, in such a case, it is difficult as well important to learn the dynamics of the gases.
Molecular nature of matter
As it is known that there are three forms of matter, they are solids, liquids, and gases. The molecules of a solid are tightly packed and they have very minimum intermolecular space among them. In liquids, the molecules are relatively less tightly packed, and hence they have relatively more intermolecular space among them. Gases on the other hand have very loosely packed molecules and the intermolecular distance among them is most as compared to the other states.

Free Path
Let’s understand what is a free path. By definition, a free path is a distance between two consecutive collisions. As known through the behavior of gases, the molecules of a gas are always in constant motion.
They collide with each other as well as with the walls of the container. Suppose molecule 1 first collided with molecule 2 and then with molecule 3 and so on. When molecule 1 collides with molecule 2, it is known as the first collision. When it collided with molecule 3, it is known as 2nd collision, and so on.
The distance between the first and the second collision is known as the free path denoted as λ1, the distance between the second and the third collision is known as λ2, and so on. Since there is no collision between any two consecutive collisions, therefore, the path is known as a free path (λ1, λ2, λ3, etc).

Mean Free Path
Mean Free Path
The mean free path is the average path covered by the molecules between collisions. It is known that there are different free paths with different path lengths. Given below are the free paths,
λ1 = First free path
λ2 = Second free path
λ3 = Third free path
λn = nth free path
The average of these path lengths is known as the mean free path. Therefore, the mean free path can (denoted by λ) be calculated as,
λ = (λ1 + λ2 + λ3 + … λn)/n
Formulae in mean free path
Let’s take the example of a single molecule having a diameter d. Imagining it moving through other molecules, considering the other molecules are still and not colliding, the molecule covers a certain distance in cylindrical form. The cross-sectional area is πd2. The volume of the cylinder is πd2 × vt, where v is the velocity of the molecule and t is the time. Let’s consider the number of molecules per unit volume is N/V. The mean free path can be written as,
λ = Length of the path/ number of collisions
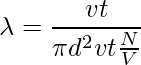
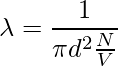
Since the characteristics of other molecules are not considered and the velocities of the numerator and denominator are different. The velocity in the numerator is average and the velocity in the denominator is relative. Therefore, a factor of √2 is added to the denominator.
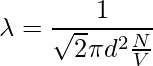
The time between two successive collisions,

The average distance between two successive collisions,
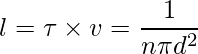
Sample Problems
Problem 1: Find the mean free path of the oxygen molecule traveling in air at 200K at 1 atm. The diameter of the oxygen molecule is 1.5 × 10-6 m.
Solution:
As the formula for the mean free path is already known, that is,
λ = 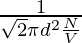
N/V is the number density that can be equated to P/KT by ideal gas law,
Therefore,
λ = 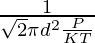
λ = 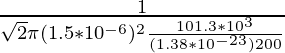
λ = 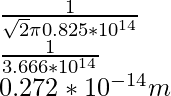
Problem 2: Find the mean free path of the oxygen molecule traveling in air at 100 K at 1 atm. The diameter of the oxygen molecule is 2 × 10-6 m.
Solution:
As the formula for the mean free path is already known, that is,
λ = 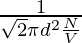
N/V is the number density that can be equated to P/KT by ideal gas law,
Therefore,
λ = 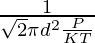
λ = 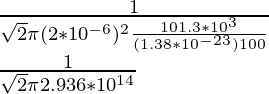
λ = 0.076 × 10-14
λ = 7.6 × 10-16m
Problem 3: Find the mean free path of the oxygen molecule traveling in air at 150 K at 1 atm. The diameter of the oxygen molecule is 1 × 10-6 m.
Solution:
As the formula for the mean free path is already known, that is,
λ = 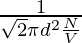
N/V is the number density that can be equated to P/KT by ideal gas law,
Therefore,
λ = 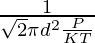
λ = 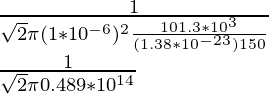
λ = 2.17 × 10-14
λ = 2.17 × 10-14m
Problem 4: If the mean free path of a molecule is given as 1.5 × 10-10 m. Find out at what temperature in pascal is the molecule traveling at 2 atm when the diameter of the molecule is given as 1.2 × 10-6 m.
Solution:
As the formula for the mean free path is already known, that is,
λ = 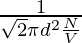
N/V is the number density that can be equated to P/KT by ideal gas law,
Therefore,
λ = 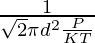
1.5 × 10-10 = 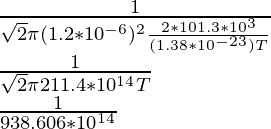
(1.5 × 10-10)(938.606 × 1014) = 1/T
1407.909 × 104 = 1/T
T = 7.10 K
Problem 5: If the mean free path of a molecule is given as 1 × 10-6 m. Find out at what temperature in pascal is the molecule traveling at 1 atm when the diameter of the molecule is given as 2 × 10-9 m.
Solution:
As the formula for the mean free path is already known, that is,
λ = 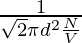
N/V is the number density that can be equated to P/KT by ideal gas law,
Therefore,
λ = 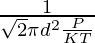
1 × 10-6 = 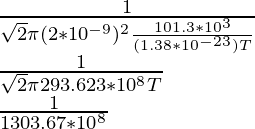
(1 × 10-6)(1303.67 × 108) = 1/T
1303.67 × 102 = 1/T
T = 7.6 × 10-6
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...