Mean Absolute Deviation
Last Updated :
10 Jun, 2023
Mean Absolute Deviation is one of the metrics of statistics that helps us find out the average spread of the data i.e., Mean Absolute Deviation shows the average distance of the observation of the dataset from the mean of the dataset. It is helpful in the analysis of data and understanding of the data with a much better understanding. Mean Absolute Deviation is one of the measures of the spread which include other measures i.e., range, quartiles, interquartile range, standard deviation, and variance. In this article, we will learn about the measure of spread which is Mean Absolute Deviation, and other than this we will also learn about the formula to find it.
What is Mean Absolute Deviation?
Mean Absolute Deviation (MAD) of a data set is the average distance between each data point of the data set and the mean of data. i.e. it represents the amount of variation that occurs around the mean value in the data set. It is also a measure of spread. It is calculated as the average of the sum of the absolute difference between each value of the data set and the mean.
What is Measure of Spread?
The measure of spread represents the amount of dispersion in a data set. i.e., how spread out are the values of the dataset around the central value (example- mean/mode/median). It tells how far away the data points tend to fall from the central value.
- The lower value of the measure of spread reflects that the data points are close to the central value. In this case, the values in a data set are more consistent.
- Further, the distance of the data points from the central value, the greater the spread. whereas here, the values are not much consistent.
Using the above diagram, we can infer that the narrow distribution represents a lower spread, and the broad distribution represents a higher spread.
Mean Absolute Deviation Formula
As Mean Absolute Deviation is the average of the absolute value of deviation about the mean of the data, its formula for grouped as well as ungrouped data is given as follows:
For Ungrouped Data
The Mean Absolute Deviation Formula for ungrouped data is given as follows:
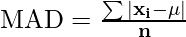
where,
- xi represents the each observation of the dataset,
- μ is the mean of the data set, and
- n is the number of observations in the data set.
For Grouped Data
The Mean Absolute Deviation Formula for grouped data is given as follows:
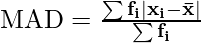
Where,
- xi represents the each observation of the dataset,
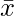 is mean of dataset
is mean of dataset- fi represents frequency of corresponding observation xi,
- 1 < i < n and n is the number of data points in the data set.
How to Calculate Mean Absolute Deviation?
To calculate the mean absolute deviation for a set of values, we can use the following steps:
Step 1: Identify whether the data set is either grouped or ungrouped and calculate the Mean.
Step 2: Calculate the absolute difference between each data point and the mean.
Step 3: Add the Absolute Difference calculated for each data point in the step 2.
Step 4: Dividing the sum of absolute difference by the number of data points given to calculate the mean abosolute deviation.
Using these steps, we can calculate the Mean Absolute Deviation of any dataset either grouped or ungrouped.
Mean Absolute Deviation vs. Standard Deviation
There are some differences between Mean Absolute Deviation and Standard Deviation, which are as follows:
Parameters
| Mean Absolute Deviation
| Standard Deviation
|
|---|
Definition
| The average distance between each
data point and the mean. | The measure of how spread out the data is from the mean. |
|---|
Calculation
| 1. Calculate the mean of the data set.
2. Calculate the absolute value of the difference
between each data point and the mean.
3. Take the average of those absolute values. | 1. Calculate the mean of the data set.
2. Calculate the difference between each data point and the mean.
3. Square each of those differences.
4. Take the average of the squared differences.
5. Take the square root of the result. |
|---|
Use
| Useful when the data set contains outliers, as it
is not affected by extreme values. | Useful when the data set does not contain outliers,
as it provides a more accurate measure of the spread of the data. |
|---|
Read More,
Solved Examples on Mean Absolute Deviation
Example 1: The data set is 11, 15, 18, 17, 12, and 17. Calculate the mean absolute deviation of the given data set.
Solution:
Step 1: Calculating the mean
x̅ = (x1 + x2 + x3 + …… + xn) / n
x̅ = (11 + 15 + 18 + 17 + 12 + 17 ) / 6
x̅ = 15
The mean of the given data = 15
Step 2: Calculating the absolute difference between each data-point and mean.
Data-Point
| Absolute Difference from the mean
|
|---|
11
| |11 – 15| = 4
|
12
| |12 – 15| = 3
|
15
| |15 – 15| = 0
|
17
| |17 – 15| = 2
|
17
| |17 – 15| = 2
|
18
| |18 – 15| = 3
|
Step 3: Adding the Absolute Difference together
(∑ |xi – mean| ) = 4 + 3 + 0 + 2 + 2 + 3
(∑ |xi – mean| ) = 14
Step 4: Dividing the sum of absolute difference and the number of data-points.
MAD = (∑ |xi – mean|) ÷ n
MAD = 14/6
MAD = 2.33
Hence, we can conclude that, on average, each data-point is 2 distance away from the mean.
Example 2: The following table shows the number of oranges that grew on Nancy’s orange tree each season
Season
| Number of Oranges
|
|---|
Winter
| 5
|
Summer
| 17
|
Spring
| 24
|
Fall
| 10
|
Find the mean absolute deviation (MAD) of the data set.
Solution:
Step 1: Calculating the mean
x̅ = (x1 + x2 + x3 + …… + xn) / n
x̅ = (5 + 17 + 24 + 10) / 4
x̅ = 56/4
The mean of the given data = 14
Step 2: Calculating the absolute difference between each data-point and mean
Data-Point
| Absolute Difference from the mean
|
|---|
5
| |5 – 14| = 9
|
17
| |17 – 14| = 3
|
24
| |24 – 14| = 10
|
10
| |10 – 14| = 4
|
Step 3:Adding the Absolute Difference together
(∑ |xi – mean| ) = 9 + 3 + 10 + 4
(∑ |xi – mean| ) = 26
Step 4: Dividing the sum of absolute difference and the number of data-points
MAD = (∑ |xi – mean| ) ÷ n
MAD = 26 / 4
MAD = 6.5
Example 3: Consider the following data.
Name of the student
| Marks in Maths
|
|---|
Chetan
| 90
|
Shubham
| 74
|
Riya
| 80
|
Manu
| 92
|
Calculate the mean absolute deviation of the given data.
Solution:
Step 1: Calculating the mean
x̅ = (x1 + x2 + x3 + …… + xn) / n
x̅ = (90 + 74 + 80 + 92) / 4
x̅ = 336/4
The mean of the given data = 84
Step 2: Calculating the absolute difference between each data-point and mean
Data-Point
| Absolute Difference from the mean
|
|---|
90
| |90 – 84| = 6
|
74
| |74 – 84| = 10
|
80
| |80 – 84| = 4
|
92
| |92 – 84| = 8
|
Step 3: Adding the Absolute Difference together
(∑ |xi – mean| ) = 6 + 10 + 4 + 8
(∑ |xi – mean| ) = 28
Step 4: Dividing the sum of absolute difference and the number of data-points
MAD = (∑ |xi – mean|) ÷ n
MAD = 28 / 4
MAD = 7
FAQs on Mean Absolute Deviation
Q1: Define Mean Absolute Deviation (MAD).
Answer:
Mean Absolute Deviation as the name suggests is the mean of the absolute value of deviation about the mean of the data set.
Q2: How is Mean Absolute Deviation (MAD) calculated?
Answer:
To calculate Mean Absolute Deviation, we need to calculate the absolute value of the deviation about the mean i.e., |xi -μ| and then find the mean of those absolute values.
Q3: What is the difference between Mean Absolute Deviation (MAD) and Standard Deviation?
Answer:
The key difference between Mean Absolute Deviation (MAD) and Standard Deviation that MAD is less sensitive to the extream values or outliers in the data. Other than that, both are the measures of spread or dispersion.
Q4: Can Mean Absolute Deviation (MAD) be negative?
Answer:
No, MAD can’t be negative as Mean Absolute Deviation is mean of absolute values.
Q5: What is the Mean Absolute Deviation of 2, 3, 8, 5, and 7?
Answer:
Mean of 2, 3, 8, 5, and 7 = (2 + 3 + 8 + 5 + 7)/5 = 25/5 = 5
Sum of Absolute deviation = |2 – 5| + |3 – 5| + |8 – 5| + |5 – 5| + |7 – 5| = 3+2+3+0+2 = 10
MAD = 10/5 = 2
Thus, MAD of 2, 3, 8, 5, and 7 is 2.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...