Maximum value of B less than A such that A ^ B = A + B
Last Updated :
21 May, 2021
Given an integer A, the task is to find the maximum value possible(B) which is less than A, such that xor of these two numbers A and B are equal to their sum, that is A ^ B = A + B.
Examples:
Input: A = 4
Output: 3
Explanation:
There are many such integers, such that A ^ B = A + B
Some of these integers are –
4 ^ 3 = 4 + 3 = 7
4 ^ 2 = 4 + 2 = 6
4 ^ 1 = 4 + 1 = 5
4 ^ 0 = 4 + 0 = 4
The maximum of these values is 3
Input: 7
Output: 0
There is no integer except 0 such that A + B = A ^ B
Approach: The idea is to use the fact that
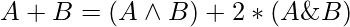 and to get the value of
and to get the value of 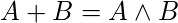 , the value of (A & B) must be equal to 0.
, the value of (A & B) must be equal to 0.
=> A & B = 0
=> B = ~A
For Example:
A = 4 (1 0 0)
B = ~ A = (0 1 1) = 3
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void maxValue(int a)
{
string c = bitset<3>(a).to_string();
string b = "";
for(int i = 0; i < c.length(); i++)
{
if ((c[i] - '0') == 1)
b += '0';
else
b += '1';
}
cout << bitset<3>(b).to_ulong();
}
int main()
{
int a = 4;
maxValue(a);
return 0;
}
|
Java
class GFG
{
static void maxValue(int a)
{
String c = Integer.toBinaryString(a);
String b = "";
for (int i = 0; i < c.length(); i++)
{
if((c.charAt(i)-'0')==1)
b +='0';
else
b+='1';
}
System.out.print(Integer.parseInt(b, 2));
}
public static void main(String []args)
{
int a = 4;
maxValue(a);
}
}
|
Python3
def maxValue(a):
a = bin(a)[2:]
b = ''
for i in list(a):
b += str(int(not int(i)))
print(int(b, 2))
return int(b, 2)
if __name__ == '__main__':
a = 4
maxValue(a)
|
C#
using System;
using System.Collections.Generic;
class GFG
{
static void maxValue(int a)
{
String c = Convert.ToString(a, 2);
String b = "";
for (int i = 0; i < c.Length; i++)
{
if((c[i] - '0') == 1)
b += '0';
else
b += '1';
}
Console.Write(Convert.ToInt32(b, 2));
}
public static void Main(String []args)
{
int a = 4;
maxValue(a);
}
}
|
Javascript
<script>
function maxValue(a)
{
var c = a.toString(2);
var b = "";
for(var i = 0; i < c.length; i++)
{
if ((c[i] - '0') == 1)
b += '0';
else
b += '1';
}
document.write(parseInt(b,2));
}
var a = 4;
maxValue(a);
</script>
|
Performance Analysis:
- Time Complexity: In the above-given approach, there is the conversion from decimal to binary which takes O(logN) time in the worst case. Therefore, the time complexity for this approach will be O(logN).
- Auxiliary Space Complexity: In the above-given approach, there is no extra space used. Therefore, the auxiliary space complexity for the above approach will be O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...