Maximum Sum of Products of two arrays by toggling adjacent bits
Last Updated :
05 Nov, 2021
Given an integer array arr1 and a binary array arr2 of same size, the task is to find the maximum possible sum of products of these arrays, i.e. (arr1[0] * arr2[0]) + (arr1[1] * arr2[1]) + ….. (arr1[N-1] * arr2[N-1]) obtained by toggling any 2 adjacent bits in the array arr2. This toggle can be done infinite number of times.
Toggling of 2 adjacent bits in array arr2 is done as follows:
- 00 is toggled to 11
- 01 is toggled to 10
- 10 is toggled to 01
- 11 is toggled to 00
Examples:
Input: arr1 = {2, 3, 1}, arr2 = {0, 0, 1}
Output: 6
Explanation:
if we put 1 corresponding to a positive integer
then arr2 will be {1, 1, 1}
No. of 1's initially and now are odd
It means parity is same
so this arrangement is fine
Hence sum will be 2 + 3 + 1 = 6.
Input: arr1 = {2, -4, 5, 3}, arr2 = {0, 1, 0, 1}
Output: 8
Approach :
- After every operation parity remains the same, i.e. no. of 1’s is even if initially it is even, or odd if initially it is odd.
- The second observation is that to toggling of i’th and j’th bit can be done by toggling from i’th bit like (i, i+1), (i+1, i+2) …. (j-1, j) here every bit is toggling twice (if bit is toggle twice then its come to its initial value) except i and j then ultimately i’th and j’th bits toggle.
- From these two observations, it can be shown that we can make any arrangement of 1’s and 0’s in array arr2. The only thing we need to take care of is the parity of ones and zeroes. The final parity must be the same as of initial parity.
- To get the maximum sum put 1 at the i’th position of arr2 if the element at the i’th position in arr1 is positive else put 0.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int maxSum(int arr1[], int arr2[], int n)
{
int initialParity = 0, finalParity = 0;
int sum = 0,
minPositive = INT_MAX,
maxNegative = INT_MIN;
for (int i = 0; i < n; i++) {
initialParity += arr2[i];
if (arr1[i] >= 0) {
finalParity += 1;
sum += arr1[i];
minPositive = min(minPositive, arr1[i]);
}
else {
maxNegative = max(maxNegative, arr1[i]);
}
}
if (initialParity % 2 == finalParity % 2) {
return sum;
}
else {
if (minPositive + maxNegative >= 0) {
return sum + maxNegative;
}
else {
return sum - minPositive;
}
}
}
int main()
{
int arr1[] = { 2, -4, 5, 3 };
int arr2[] = { 0, 1, 0, 1 };
int n = sizeof(arr1) / sizeof(arr1[0]);
cout << maxSum(arr1, arr2, n) << endl;
return 0;
}
|
Java
class GFG
{
static int maxSum(int arr1[],
int arr2[], int n)
{
int initialParity = 0, finalParity = 0;
int sum = 0,
minPositive = Integer.MAX_VALUE,
maxNegative = Integer.MIN_VALUE;
for (int i = 0; i < n; i++)
{
initialParity += arr2[i];
if (arr1[i] >= 0)
{
finalParity += 1;
sum += arr1[i];
minPositive = Math.min(minPositive,
arr1[i]);
}
else
{
maxNegative = Math.max(maxNegative,
arr1[i]);
}
}
if (initialParity % 2 == finalParity % 2)
{
return sum;
}
else
{
if (minPositive + maxNegative >= 0)
{
return sum + maxNegative;
}
else
{
return sum - minPositive;
}
}
}
public static void main(String []args)
{
int arr1[] = { 2, -4, 5, 3 };
int arr2[] = { 0, 1, 0, 1 };
int n = arr1.length;
System.out.println(maxSum(arr1, arr2, n));
}
}
|
Python3
import sys
def maxSum(arr1, arr2, n) :
initialParity, finalParity = 0, 0
sum = 0
minPositive = sys.maxsize
maxNegative = -sys.maxsize - 1
for i in range(n) :
initialParity += arr2[i];
if (arr1[i] >= 0) :
finalParity += 1
sum += arr1[i]
minPositive = min(minPositive, arr1[i])
else :
maxNegative = max(maxNegative, arr1[i])
if (initialParity % 2 == finalParity % 2) :
return sum
else :
if (minPositive + maxNegative >= 0) :
return sum + maxNegative
else :
return sum - minPositive
arr1 = [ 2, -4, 5, 3 ]
arr2 = [ 0, 1, 0, 1 ]
n = len(arr1)
print(maxSum(arr1, arr2, n))
|
C#
using System;
class GFG
{
static int maxSum(int []arr1,
int []arr2, int n)
{
int initialParity = 0, finalParity = 0;
int sum = 0,
minPositive = int.MaxValue,
maxNegative = int.MinValue;
for (int i = 0; i < n; i++)
{
initialParity += arr2[i];
if (arr1[i] >= 0)
{
finalParity += 1;
sum += arr1[i];
minPositive = Math.Min(minPositive,
arr1[i]);
}
else
{
maxNegative = Math.Max(maxNegative,
arr1[i]);
}
}
if (initialParity % 2 == finalParity % 2)
{
return sum;
}
else
{
if (minPositive + maxNegative >= 0)
{
return sum + maxNegative;
}
else
{
return sum - minPositive;
}
}
}
public static void Main(String []args)
{
int []arr1 = { 2, -4, 5, 3 };
int []arr2 = { 0, 1, 0, 1 };
int n = arr1.Length;
Console.WriteLine(maxSum(arr1, arr2, n));
}
}
|
Javascript
<script>
function maxSum(arr1, arr2, n) {
let initialParity = 0, finalParity = 0;
let sum = 0,
minPositive = Number.MAX_SAFE_INTEGER,
maxNegative = Number.MIN_SAFE_INTEGER;
for (let i = 0; i < n; i++) {
initialParity += arr2[i];
if (arr1[i] >= 0) {
finalParity += 1;
sum += arr1[i];
minPositive = Math.min(minPositive,
arr1[i]);
}
else {
maxNegative = Math.max(maxNegative,
arr1[i]);
}
}
if (initialParity % 2 == finalParity % 2) {
return sum;
}
else {
if (minPositive + maxNegative >= 0) {
return sum + maxNegative;
}
else {
return sum - minPositive;
}
}
}
let arr1 = [2, -4, 5, 3];
let arr2 = [0, 1, 0, 1];
let n = arr1.length;
document.write(maxSum(arr1, arr2, n));
</script>
|
Time Complexity: 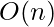 , where n is the size of the array.
, where n is the size of the array.
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...