Maximum String Partition
Last Updated :
22 Dec, 2022
Given a string. The task is to find the maximum number P, such that a given string can be partitioned into P contiguous substrings such that any two adjacent substrings must be different. More formally, 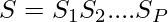 and
and 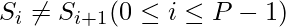 .
.
Examples:
Input: str = “aabccd”
Output: 4
Explanation:
We can divide the given string into four strings, like “a”, “ab”, “c”, “cd”. We can not divide
it are more than four parts. If we do, then the condition 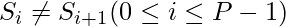 will not
will not
satisfy
Input: str = “aaaa”
Output: 3
Approach:
- Here we only have to focus on the value of P, not upon finding those P substrings.
- We will solve it greedily. We always check the current string that we have with the previous string that has been taken already.
- If we find that both of them are the same, then we will go forward, otherwise, create a partition here, and change the previous track of the string to the current string, which means we will treat this current string as the previous string for future comparison.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int maxPartition(string s)
{
int n = s.length(), P = 0;
string current = "", previous = "";
for (int i = 0; i < n; i++) {
current += s[i];
if (current != previous) {
previous = current;
current.clear();
P++;
}
}
return P;
}
int main()
{
string s = "geeksforgeeks";
int ans = maxPartition(s);
cout << ans << "\n";
return 0;
}
|
Java
class GFG
{
static int maxPartition(String s)
{
int n = s.length(), P = 0;
String current = "", previous = "";
for (int i = 0; i < n; i++)
{
current += s.charAt(i);
if (!current.equals(previous))
{
previous = current;
current = "";
P++;
}
}
return P;
}
public static void main (String[] args)
{
String s = "geeksforgeeks";
int ans = maxPartition(s);
System.out.println(ans);
}
}
|
Python3
def maxPartition(s):
n = len(s)
P = 0
current = ""
previous = ""
for i in range(n):
current += s[i]
if (current != previous):
previous = current
current = ""
P += 1
return P
s = "geeksforgeeks"
ans = maxPartition(s)
print(ans)
|
C#
using System;
class GFG
{
static int maxPartition(string s)
{
int n = s.Length, P = 0;
string current = "", previous = "";
for (int i = 0; i < n; i++)
{
current += s[i];
if (!current.Equals(previous))
{
previous = current;
current = "";
P++;
}
}
return P;
}
public static void Main ()
{
string s = "geeksforgeeks";
int ans = maxPartition(s);
Console.WriteLine(ans);
}
}
|
Javascript
<script>
function maxPartition(s)
{
var n = s.length, P = 0;
var current = "", previous = "";
for (var i = 0; i < n; i++) {
current += s[i];
if (current != previous) {
previous = current;
current = "";
P++;
}
}
return P;
}
var s = "geeksforgeeks";
var ans = maxPartition(s);
document.write( ans);
</script>
|
Time Complexity: O(N), where N is the length of the string.
Auxiliary Space: O(N), where N is the length of the given string.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...