Maximum Product Cutting | DP-36
Last Updated :
19 Apr, 2024
Given a rope of length n meters, cut the rope in different parts of integer lengths in a way that maximizes product of lengths of all parts. You must make at least one cut. Assume that the length of rope is more than 2 meters.
Examples:
Input: n = 2
Output: 1 (Maximum obtainable product is 1*1)
Input: n = 3
Output: 2 (Maximum obtainable product is 1*2)
Input: n = 4
Output: 4 (Maximum obtainable product is 2*2)
Input: n = 5
Output: 6 (Maximum obtainable product is 2*3)
Input: n = 10
Output: 36 (Maximum obtainable product is 3*3*4)
1) Optimal Substructure:
This problem is similar to Rod Cutting Problem. We can get the maximum product by making a cut at different positions and comparing the values obtained after a cut. We can recursively call the same function for a piece obtained after a cut.
Let maxProd(n) be the maximum product for a rope of length n. maxProd(n) can be written as following.
maxProd(n) = max(i*(n-i), maxProdRec(n-i)*i) for all i in {1, 2, 3 .. n}
2) Overlapping Subproblems:
Following is simple recursive implementation of the problem. The implementation simply follows the recursive structure mentioned above.
C++
// A Naive Recursive method to find maximum product
#include <iostream>
using namespace std;
// Utility function to get the maximum of two and three integers
int max(int a, int b) { return (a > b)? a : b;}
int max(int a, int b, int c) { return max(a, max(b, c));}
// The main function that returns maximum product obtainable
// from a rope of length n
int maxProd(int n)
{
// Base cases
if (n == 0 || n == 1) return 0;
// Make a cut at different places and take the maximum of all
int max_val = 0;
for (int i = 1; i < n; i++)
max_val = max(max_val, i*(n-i), maxProd(n-i)*i);
// Return the maximum of all values
return max_val;
}
/* Driver program to test above functions */
int main()
{
cout << "Maximum Product is " << maxProd(10);
return 0;
}
// Java program to find maximum product
import java.io.*;
class GFG {
// The main function that returns
// maximum product obtainable from
// a rope of length n
static int maxProd(int n)
{
// Base cases
if (n == 0 || n == 1) return 0;
// Make a cut at different places
// and take the maximum of all
int max_val = 0;
for (int i = 1; i < n; i++)
max_val = Math.max(max_val,
Math.max(i * (n - i),
maxProd(n - i) * i));
// Return the maximum of all values
return max_val;
}
/* Driver program to test above functions */
public static void main(String[] args)
{
System.out.println("Maximum Product is "
+ maxProd(10));
}
}
// This code is contributed by Prerna Saini
# The main function that returns maximum
# product obtainable from a rope of length n
def maxProd(n):
# Base cases
if (n == 0 or n == 1):
return 0
# Make a cut at different places
# and take the maximum of all
max_val = 0
for i in range(1, n - 1):
max_val = max(max_val, max(i * (n - i), maxProd(n - i) * i))
#Return the maximum of all values
return max_val;
# Driver program to test above functions
print("Maximum Product is ", maxProd(10));
# This code is contributed
# by Sumit Sudhakar
// C# program to find maximum product
using System;
class GFG {
// The main function that returns
// the max possible product
static int maxProd(int n)
{
// n equals to 2 or 3 must
// be handled explicitly
if (n == 2 || n == 3)
return (n - 1);
// Keep removing parts of size
// 3 while n is greater than 4
int res = 1;
while (n > 4) {
n -= 3;
// Keep multiplying 3 to res
res *= 3;
}
// The last part multiplied
// by previous parts
return (n * res);
}
// Driver code
public static void Main()
{
Console.WriteLine("Maximum Product is "
+ maxProd(10));
}
}
// This code is contributed by Sam007
<script>
// Javascript program to find maximum product
// The main function that returns
// maximum product obtainable from
// a rope of length n
function maxProd(n)
{
// Base cases
if (n == 0 || n == 1)
return 0;
// Make a cut at different places
// and take the maximum of all
let max_val = 0;
for (let i = 1; i < n; i++)
{
max_val = Math.max(max_val,
Math.max(i * (n - i),
maxProd(n - i) * i));
}
// Return the maximum of all values
return max_val;
}
/* Driver program to test above functions */
document.write("Maximum Product is "
+ maxProd(10));
// This code is contributed by rag2127
</script>
<?php
// A Naive Recursive method to
// find maximum product
// Utility function to get the
// maximum of two and three integers
function max_1($a, $b, $c)
{
return max($a, max($b, $c));
}
// The main function that returns
// maximum product obtainable
// from a rope of length n
function maxProd($n)
{
// Base cases
if ($n == 0 || $n == 1) return 0;
// Make a cut at different places
// and take the maximum of all
$max_val = 0;
for ($i = 1; $i < $n; $i++)
$max_val = max_1($max_val, $i * ($n - $i),
maxProd($n - $i) * $i);
// Return the maximum of all values
return $max_val;
}
// Driver Code
echo "Maximum Product is " . maxProd(10);
// This code is contributed
// by ChitraNayal
?>
OutputMaximum Product is 36
Time complexity: O(n^2)
The time complexity of the maxProd function is O(n^2), because it contains a loop that iterates n-1 times, and inside the loop it calls itself recursively with a smaller input size (n-i). The maximum recursion depth is n, so the total time complexity is n * (n-1) = O(n^2).
Space complexity: O(n)
The space complexity of the maxProd function is O(n), because the maximum recursion depth is n, and each recursive call adds a new activation record to the call stack, which contains local variables and return addresses. Therefore, the space used by the call stack is proportional to the input size n.
Considering the above implementation, following is recursion tree for a Rope of length 5.
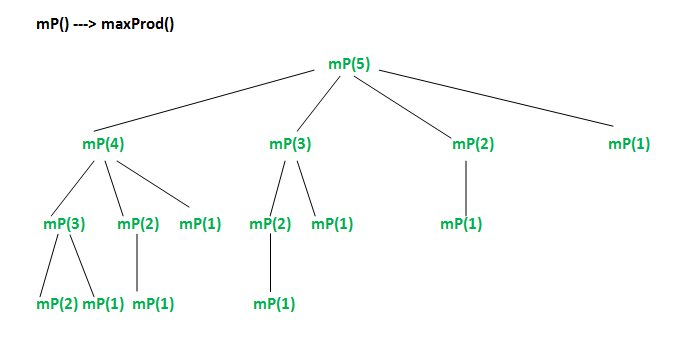
In the above partial recursion tree, mP(3) is being solved twice. We can see that there are many subproblems which are solved again and again. Since same subproblems are called again, this problem has Overlapping Subproblems property. So the problem has both properties (see this and this) of a dynamic programming problem. Like other typical Dynamic Programming(DP) problems, recomputations of same subproblems can be avoided by constructing a temporary array val[] in bottom up manner.
C++
// C++ code to implement the approach\
// A Dynamic Programming solution for Max Product Problem
int maxProd(int n)
{
int val[n+1];
val[0] = val[1] = 0;
// Build the table val[] in bottom up manner and return
// the last entry from the table
for (int i = 1; i <= n; i++)
{
int max_val = 0;
for (int j = 1; j <= i; j++)
max_val = max(max_val, (i-j)*j, j*val[i-j]);
val[i] = max_val;
}
return val[n];
}
// This code is contributed by sanjoy_62.
// A Dynamic Programming solution for Max Product Problem
int maxProd(int n)
{
int val[n+1];
val[0] = val[1] = 0;
// Build the table val[] in bottom up manner and return
// the last entry from the table
for (int i = 1; i <= n; i++)
{
int max_val = 0;
for (int j = 1; j <= i; j++)
max_val = max(max_val, (i-j)*j, j*val[i-j]);
val[i] = max_val;
}
return val[n];
}
// A Dynamic Programming solution for Max Product Problem
int maxProd(int n)
{
int val[n+1];
val[0] = val[1] = 0;
// Build the table val[] in bottom up manner and return
// the last entry from the table
for (int i = 1; i <= n; i++)
{
int max_val = 0;
for (int j = 1; j <= i; j++)
max_val = Math.max(max_val, (i-j)*j, j*val[i-j]);
val[i] = max_val;
}
return val[n];
}
// This code is contributed by umadevi9616
# A Dynamic Programming solution for Max Product Problem
def maxProd(n):
val= [0 for i in range(n+1)];
# Build the table val in bottom up manner and return
# the last entry from the table
for i in range(1,n+1):
max_val = 0;
for j in range(1,i):
max_val = max(max_val, (i-j)*j, j*val[i-j]);
val[i] = max_val;
return val[n];
# This code is contributed by gauravrajput1
// A Dynamic Programming solution for Max Product Problem
int maxProd(int n)
{
int []val = new int[n+1];
val[0] = val[1] = 0;
// Build the table val[] in bottom up manner and return
// the last entry from the table
for (int i = 1; i <= n; i++)
{
int max_val = 0;
for (int j = 1; j <= i; j++)
max_val = Math.Max(max_val, (i-j)*j, j*val[i-j]);
val[i] = max_val;
}
return val[n];
}
// This code is contributed by umadevi9616
<script>
// A Dynamic Programming solution for Max Product Problem
function maxProd(n)
{
var val = Array(n+1).fill(0);
val[0] = val[1] = 0;
// Build the table val in bottom up manner and return
// the last entry from the table
for (var 1; i <= n; i++)
{
var max_val = 0;
for ( var ; j <= i; j++)
max_val = Math.max(max_val, (i-j)*j, j*val[i-j]);
val[i] = max_val;
}
return val[n];
}
// This code is contributed by gauravrajput1
// This code is modified by Susobhan Akhuli
</script>
Time Complexity of the Dynamic Programming solution is O(n^2) and it requires O(n) extra space.
A Tricky Solution:
If we see some examples of this problems, we can easily observe following pattern.
The maximum product can be obtained be repeatedly cutting parts of size 3 while size is greater than 4, keeping the last part as size of 2 or 3 or 4. For example, n = 10, the maximum product is obtained by 3, 3, 4. For n = 11, the maximum product is obtained by 3, 3, 3, 2. Following is the implementation of this approach.
C++
#include <iostream>
using namespace std;
/* The main function that returns the max possible product */
int maxProd(int n)
{
// n equals to 2 or 3 must be handled explicitly
if (n == 2 || n == 3) return (n-1);
// Keep removing parts of size 3 while n is greater than 4
int res = 1;
while (n > 4)
{
n -= 3;
res *= 3; // Keep multiplying 3 to res
}
return (n * res); // The last part multiplied by previous parts
}
/* Driver program to test above functions */
int main()
{
cout << "Maximum Product is " << maxProd(10);
return 0;
}
// Java program to find maximum product
import java.io.*;
class GFG {
/* The main function that returns the
max possible product */
static int maxProd(int n)
{
// n equals to 2 or 3 must be handled
// explicitly
if (n == 2 || n == 3) return (n-1);
// Keep removing parts of size 3
// while n is greater than 4
int res = 1;
while (n > 4)
{
n -= 3;
// Keep multiplying 3 to res
res *= 3;
}
// The last part multiplied by
// previous parts
return (n * res);
}
/* Driver program to test above functions */
public static void main(String[] args)
{
System.out.println("Maximum Product is "
+ maxProd(10));
}
}
// This code is contributed by Prerna Saini
# The main function that returns the
# max possible product
def maxProd(n):
# n equals to 2 or 3 must
# be handled explicitly
if (n == 2 or n == 3):
return (n - 1)
# Keep removing parts of size 3
# while n is greater than 4
res = 1
while (n > 4):
n -= 3;
# Keep multiplying 3 to res
res *= 3;
# The last part multiplied
# by previous parts
return (n * res)
# Driver program to test above functions
print("Maximum Product is ", maxProd(10));
# This code is contributed
# by Sumit Sudhakar
// C# program to find maximum product
using System;
class GFG {
// The main function that returns
// maximum product obtainable from
// a rope of length n
static int maxProd(int n)
{
// Base cases
if (n == 0 || n == 1)
return 0;
// Make a cut at different places
// and take the maximum of all
int max_val = 0;
for (int i = 1; i < n; i++)
max_val = Math.Max(max_val,
Math.Max(i * (n - i),
maxProd(n - i) * i));
// Return the maximum of all values
return max_val;
}
// Driver code
public static void Main()
{
Console.WriteLine("Maximum Product is "
+ maxProd(10));
}
}
// This code is contributed by Sam007
<script>
// Javascript program to find maximum product
/* The main function that returns the
max possible product */
function maxProd(n)
{
// n equals to 2 or 3 must be handled
// explicitly
if (n == 2 || n == 3)
{
return (n-1);
}
// Keep removing parts of size 3
// while n is greater than 4
let res = 1;
while (n > 4)
{
n -= 3;
// Keep multiplying 3 to res
res *= 3;
}
// The last part multiplied by
// previous parts
return (n * res);
}
/* Driver program to test above functions */
document.write("Maximum Product is " + maxProd(10));
// This code is contributed by avanitrachhadiya2155
</script>
<?php
/* The main function that returns
the max possible product */
function maxProd($n)
{
// n equals to 2 or 3 must
// be handled explicitly
if ($n == 2 || $n == 3)
return ($n - 1);
// Keep removing parts of size
// 3 while n is greater than 4
$res = 1;
while ($n > 4)
{
$n = $n - 3;
// Keep multiplying 3 to res
$res = $res * 3;
}
// The last part multiplied
// by previous parts
return ($n * $res);
}
// Driver code
echo ("Maximum Product is ");
echo(maxProd(10));
// This code is contributed
// by Shivi_Aggarwal
?>
OutputMaximum Product is 36
Time Complexity: O(n/3) ~= O(n), as here in every loop step we do decrement of 3 from n so it’s take n/3 – 1 iteration to make n less than or equal to 4 so ultimately we need O(n) time complexity.
Space Complexity: O(1), as we don’t need any extra space to generate answer
More Efficient Solution (log(n) time complexity solution)
In the above solution, we are using a while loop in which on every iteration of look we are subtracting 3 from n and multiplying the result with 3. But If we observe mathematically then, for any number n, we can subtract (n/3) times 3 from that number. so using this observation we can eliminate that while loop from the code and instead of that we directly do (n/3) times 3 subtraction from n. so after knowing that number we can use the pow() function to multiply the result which takes log(n) time complexity to multiply. here the while loop break condition is (n>4) so we need to handle that case by the if-else statement as shown in the code.
C++
#include <bits/stdc++.h>
using namespace std;
/* The main function that returns the max possible product
*/
int maxProd(int n)
{
// edge case
if ((n == 2) || (n == 3)) {
return n - 1;
}
// how many times we can subtract 3 from n is (n/3)
int num_threes = n / 3;
int num_twos = 0;
// specifically for handling case where n = 4, 7, 10,
// ...
if (n % 3 == 1) {
num_threes -= 1;
num_twos = 2;
}
// specifically for handling case where n = 5, 8, 11,
// ...
else if (n % 3 == 2) {
num_twos = 1;
}
int res = 1;
res *= pow(3, num_threes);
res *= pow(2, num_twos);
return res;
}
/* Driver program to test above functions */
int main()
{
cout << "Maximum Product is " << maxProd(10);
return 0;
}
// Java Program for the above approach
import java.lang.Math;
public class Main {
public static void main(String[] args) {
System.out.println("Maximum Product is " + maxProd(10));
}
/* The main function that returns the max possible product */
public static int maxProd(int n) {
// edge case
if ((n == 2) || (n == 3)) {
return n - 1;
}
// how many times we can subtract 3 from n is (n/3)
int num_threes = n / 3;
int num_twos = 0;
// specifically for handling case where n = 4, 7, 10,
// ...
if (n % 3 == 1) {
num_threes -= 1;
num_twos = 2;
}
// specifically for handling case where n = 5, 8, 11,
// ...
else if (n % 3 == 2) {
num_twos = 1;
}
int res = 1;
res *= Math.pow(3, num_threes);
res *= Math.pow(2, num_twos);
return res;
}
}
// Contributed by adityasharmadev01
import math
def max_prod(n):
"""
The main function that returns the max possible product
"""
# edge case
if n == 2 or n == 3:
return n - 1
# how many times we can subtract 3 from n is (n/3)
num_threes = n // 3
num_twos = 0
# specifically for handling case where n = 4, 7, 10, ...
if n % 3 == 1:
num_threes -= 1
num_twos = 2
# specifically for handling case where n = 5, 8, 11, ...
elif n % 3 == 2:
num_twos = 1
res = 1
res *= math.pow(3, num_threes)
res *= math.pow(2, num_twos)
return int(res)
# Driver program to test above function
print("Maximum Product is", max_prod(10))
using System;
public class Program {
public static void Main(string[] args)
{
Console.WriteLine("Maximum Product is "
+ maxProd(10));
}
/* The main function that returns the max possible
* product */
public static int maxProd(int n)
{
// edge case
if ((n == 2) || (n == 3)) {
return n - 1;
}
// how many times we can subtract 3 from n is (n/3)
int num_threes = n / 3;
int num_twos = 0;
// specifically for handling case where n = 4, 7,
// 10,
// ...
if (n % 3 == 1) {
num_threes -= 1;
num_twos = 2;
}
// specifically for handling case where n = 5, 8,
// 11,
// ...
else if (n % 3 == 2) {
num_twos = 1;
}
int res = 1;
res *= (int)Math.Pow(3, num_threes);
res *= (int)Math.Pow(2, num_twos);
return res;
}
}
function maxProd(n) {
// edge case
if ((n == 2) || (n == 3)) {
return n - 1;
}
// how many times we can subtract 3 from n is (n/3)
let num_threes = Math.floor(n / 3);
let num_twos = 0;
// specifically for handling case where n = 4, 7, 10,
// ...
if (n % 3 == 1) {
num_threes -= 1;
num_twos = 2;
}
// specifically for handling case where n = 5, 8, 11,
// ...
else if (n % 3 == 2) {
num_twos = 1;
}
let res = 1;
res *= Math.pow(3, num_threes);
res *= Math.pow(2, num_twos);
return res;
}
console.log("Maximum Product is " + maxProd(10));
OutputMaximum Product is 36
Time Complexity: O(log(n)), the pow() function takes log(n) time complexity so overall time complexity is O(log(n)).
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...