Maximum points of intersections possible among X circles and Y straight lines
Last Updated :
12 Jan, 2023
Given two integers X and Y, the task is to find the maximum number of points of intersection possible among X circles and Y straight lines.
Example:
Input: X = 4, Y = 4
Output: 50
Explanation:
4 lines intersect each other at 6 points and 4 circles intersect each other at maximum of 12 points.
Each line intersects 4 circles at 8 points.
Hence, 4 lines intersect four circles at a maximum of 32 points.
Thus, required number of intersections = 6 + 12 + 32 = 50.
Input: X = 3, Y = 4
Output: 36
Approach:
It can be observed that there are three types of intersections:
- The number of ways to choose a pair of points from X circles is
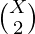 . Each such pair intersect at most two points.
. Each such pair intersect at most two points. - The number of ways to choose a pair of points from Y lines is
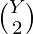 . Each such pair intersect in at most one point.
. Each such pair intersect in at most one point. - The number of ways to choose one circle and one line from X circles and Y lines is
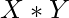 . Each such pair intersect in at most two points.
. Each such pair intersect in at most two points.
So, the maximum number of point of intersection can be calculated as:
=> 
=> 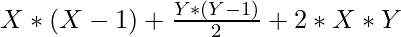
Thus, formula to find maximum number of point of intersection of X circles and Y straight lines is:
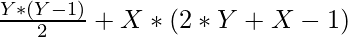
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int maxPointOfIntersection(int x, int y)
{
int k = y * (y - 1) / 2;
k = k + x * (2 * y + x - 1);
return k;
}
int main()
{
int x = 3;
int y = 4;
cout << (maxPointOfIntersection(x, y));
}
|
Java
import java.io.*;
public class GFG{
static int maxPointOfIntersection(int x, int y)
{
int k = y * (y - 1) / 2;
k = k + x * (2 * y + x - 1);
return k;
}
public static void main(String[] args)
{
int x = 3;
int y = 4;
System.out.print(maxPointOfIntersection(x, y));
}
}
|
Python3
def maxPointOfIntersection(x, y):
k = y * ( y - 1 ) // 2
k = k + x * ( 2 * y + x - 1 )
return k
x = 3
y = 4
print(maxPointOfIntersection(x, y))
|
C#
using System;
class GFG{
static int maxPointOfIntersection(int x, int y)
{
int k = y * (y - 1) / 2;
k = k + x * (2 * y + x - 1);
return k;
}
public static void Main(String[] args)
{
int x = 3;
int y = 4;
Console.Write(maxPointOfIntersection(x, y));
}
}
|
Javascript
<script>
function maxPointOfIntersection(x, y)
{
let k = y * (y - 1) / 2;
k = k + x * (2 * y + x - 1);
return k;
}
let x = 3;
let y = 4;
document.write(maxPointOfIntersection(x, y));
</script>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...