Maximum number of region in which N non-parallel lines can divide a plane
Last Updated :
28 Jul, 2022
Given N‘, the number of non-parallel lines. The task is to find the maximum number of regions in which these lines can divide a plane.
Examples:
Input : N = 3
Output : 7
Input : N = 2
Output : 4
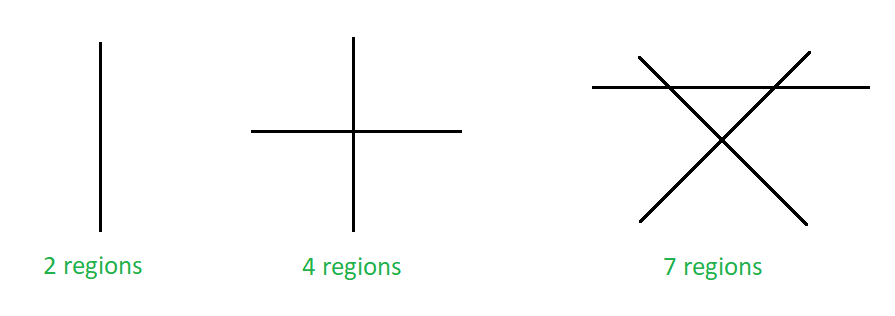
Maximum number of regions on a plane formed due to non-parallel lines
Approach: The above image shows the maximum number of regions a line can divide a plane. One line can divide a plane into two regions, two non-parallel lines can divide a plane into 4 regions and three non-parallel lines can divide into 7 regions, and so on. When the nth line is added to a cluster of (n-1) lines then the maximum number of extra regions formed is equal to n.
Now solve the recursion as follows:
L(2) – L(1) = 2 … (i)
L(3) – L(2) = 3 … (ii)
L(4) – L(3) = 4 … (iii)
. . .
. . .
L(n) – L(n-1) = n ; … (n)
Adding all the above equation we get,
L(n) – L(1) = 2 + 3 + 4 + 5 + 6 + 7 + …… + n ;
L(n) = L(1) + 2 + 3 + 4 + 5 + 6 + 7 + …… + n ;
L(n) = 2 + 2 + 3 + 4 + 5 + 6 + 7 + …… + n ;
L(n) = 1 + 2 + 3 + 4 + 5 + 6 + 7 + …… + n + 1 ;
L(n) = n ( n + 1 ) / 2 + 1 ;
The number of region in which N non-parallel lines can divide a plane is equal to N*( N + 1 )/2 + 1.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void maxRegions(int n)
{
int num;
num = n * (n + 1) / 2 + 1;
cout << num;
}
int main()
{
int n = 10;
maxRegions(n);
return 0;
}
|
Java
class GFG
{
static void maxRegions(int n)
{
int num;
num = n * (n + 1) / 2 + 1;
System.out.println(num);;
}
public static void main(String[] args)
{
int n = 10;
maxRegions(n);
}
}
|
Python3
def maxRegions(n):
num = n * (n + 1) // 2 + 1
print(num)
n = 10
maxRegions(n)
|
C#
using System;
class GFG
{
static void maxRegions(int n)
{
int num;
num = n * (n + 1) / 2 + 1;
Console.WriteLine(num);
}
public static void Main(String[] args)
{
int n = 10;
maxRegions(n);
}
}
|
Javascript
<script>
function maxRegions(n)
{
let num;
num = parseInt( n * (n + 1) / 2) + 1;
document.write(num);
}
let n = 10;
maxRegions(n);
</script>
|
Time Complexity : O(1)
Space Complexity : O(1) since using constant variables
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...