Maximum number of elements greater than X after equally distributing subset of array

Given an array, arr[] and an integer X, the task is to count the number of elements greater than X after equally dividing the subset of elements. That is each element of the subset will be equal to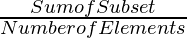 

Examples:

Input: arr[] = {5, 1, 2, 1}, X = 3 
Output: 2 
Explanation:
Subset which is equally distributes is {5, 2}. 
After which the elements will be 3.5 each. 
Array => {3.5, 1, 3.5, 1} 
Total number of elements greater than X = 2

Input: arr[] = {3, 4, 5}, X = 6 
Output: 0 
Explanation:
There is no way to distribute any subset of array to make the elements greater than 6. 

Approach: The idea is to sort the array and include the largest elements of the array such that their average is greater than or equal to X. Count of such elements whose average is greater than or equal to X is the desired subset which can be equally divided and each element is greater than X.

Below is the implementation of the above approach: 

C++

// C++ implementation to find the
// maximum number of elements greater
// than X by equally distributing

#include <bits/stdc++.h>
using namespace std;

// Function to find the
// maximum number of elements greater
// than X by equally distributing
void redistribute(int arr[], int n, int x)
{
    // Sorting the array
    sort(arr, arr + n, greater<int>());

    int i, sum = 0;

    // Loop to iterate over the elements
    // of the array
    for (i = 0; i < n; i++) {
        sum += arr[i];

        // If no more elements can
        // become larger than x
        if (sum / (i + 1) < x) {
            cout << i << endl;
            break;
        }
    }
    if (i == n)
        cout << n << endl;
}

// Driver Code
int main()
{
    int arr[] = { 5, 1, 2, 1 };
    int x = 3;
    redistribute(arr, 4, x);
    return 0;
}

Java

// Java implementation to find the
// maximum number of elements greater
// than X by equally distributing
import java.util.*;

class GFG{

// Function to find the maximum
// number of elements greater
// than X by equally distributing
static void redistribute(Integer arr[], int n,
                                        int x)
{

    // Sorting the array
    Arrays.sort(arr, Collections.reverseOrder());

    int i, sum = 0;

    // Loop to iterate over the elements
    // of the array
    for(i = 0; i < n; i++)
    {
       sum += arr[i];

       // If no more elements can
       // become larger than x
       if (sum / (i + 1) < x)
       {
           System.out.print(i + "\n");
           break;
       }
    }
    if (i == n)
        System.out.print(n + "\n");
}

// Driver Code
public static void main(String[] args)
{
    Integer arr[] = { 5, 1, 2, 1 };
    int x = 3;

    redistribute(arr, 4, x);
}
}

// This code is contributed by Rajput-Ji

Python3

# Python3 implementation to find the
# maximum number of elements greater
# than X by equally distributing

# Function to find the
# maximum number of elements greater
# than X by equally distributing
def redistribute(arr, n, x):

    # Sorting the array
    arr.sort(reverse = True)

    sum = 0

    # Loop to iterate over the
    # elements of the array
    for i in range(n):
        sum += arr[i]

        # If no more elements can
        # become larger than x
        if (sum / (i + 1) < x):
            print(i)
            break

    if (i == n):
        print(n)

# Driver Code
arr = [ 5, 1, 2, 1 ]
x = 3

# Function call
redistribute(arr, 4, x)

# This code is contributed by Vishal Maurya.

C#

// C# implementation to find the
// maximum number of elements greater
// than X by equally distributing
using System;

class GFG{

// Function to find the maximum
// number of elements greater
// than X by equally distributing
static void redistribute(int []arr, int n,
                                    int x)
{

    // Sorting the array
    Array.Sort(arr);
    Array.Reverse(arr);

    int i, sum = 0;

    // Loop to iterate over the elements
    // of the array
    for(i = 0; i < n; i++)
    {
       sum += arr[i];

       // If no more elements can
       // become larger than x
       if (sum / (i + 1) < x)
       {
           Console.Write(i + "\n");
           break;
       }
    }
    if (i == n)
        Console.Write(n + "\n");
}

// Driver Code
public static void Main(String[] args)
{
    int []arr = { 5, 1, 2, 1 };
    int x = 3;

    redistribute(arr, 4, x);
}
}

// This code is contributed by Rajput-Ji

Javascript

<script>

// JavaScript implementation to find the
// maximum number of elements greater
// than X by equally distributing

// Function to find the maximum
// number of elements greater
// than X by equally distributing
function redistribute(arr, n, x)
{

    // Sorting the array
    arr.sort();
    arr.reverse();

    let i, sum = 0;

    // Loop to iterate over the elements
    // of the array
    for(i = 0; i < n; i++)
    {
        sum += arr[i];

        // If no more elements can
        // become larger than x
        if ((sum / (i + 1)) < x)
        {
            document.write(i );
            break;
        }
    }
    if (i == n)
        document.write(n);
}

// Driver Code
let arr = [ 5, 1, 2, 1 ];
let x = 3;

redistribute(arr, 4, x);

// This code is contributed by sanjoy_62

</script>

Output:

2

Time Complexity: O(n*log(n))
Auxiliary Space: O(1)