Maximum number of edges to be removed to contain exactly K connected components in the Graph

Difficulty Level : Medium
Last Updated : 04 Feb, 2021

Given an undirected graph G with N nodes, M edges, and an integer K, the task is to find the maximum count of edges that can be removed such that there remains exactly K connected components after the removal of edges. If the graph cannot contain K connect components, print -1.

Examples:

Input: N = 4, M = 3, K = 2, Edges[][] = {{1, 2}, {2, 3}, {3, 4}}

Output: 1
Explanation:
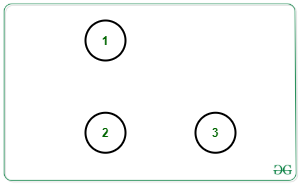
One possible way is to remove edge [1, 2]. Then there will be 2 connect components as shown below:

Input: N = 3, M = 3, K = 3, Edges[][] = {{1, 2}, {2, 3}, {3, 1}}

Output: 3
Explanation: All edges can be removed to make 3 connected components as shown below:

Approach: To solve the given problem, count the number of connected components present in the given graph. Let the count be C. Observe that if C is greater than K then no possible edge removal can generate K connected components as the number of connected components will only increase. Otherwise, the answer will always exist.

Following observations need to be made in order to solve the problem:

Suppose C₁, C₂, …, C_c, are the number of node in each connected component. Then, each component must have edges as C₁– 1, C₂– 1, …, C_c-1 after edges are removed. Therefore,

C₁ – 1 + C₂ – 1 + … + C_c – 1 = C₁ + C₂ + … + C_c – C = N – C, where N is the number of nodes.

The above condition will give us the C connected components by removing M – (N – C) edges as N – C edges are needed to make C components. To get K components, (K – C) more edges must be removed.
Hence, the total count of edges to be removed is given by:

M – (N – C) + (K – C) = M – N + K

Follow the steps below to solve the problem:

Count the number of connected components present in the given graph. Let the count be C.
If C is greater than K, print -1.
Else print M – N + K where N is the number f nodes, M is the number of edges and K is the required number of connected components.

Below is the implementation of the above approach:

C++

// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
 
class Graph
{
  public:
    int V;
    map<int, vector<int>> adj;
 
    Graph(int);
    void addEdge(int, int);
    void DFS(int, vector<bool> &);
} * g;
 
// Constructor
Graph::Graph(int V)
{
   
  // No. of vertices
  this->V = V;
   
  // Dictionary of lists
  for(int i = 1; i <= V; i++)
    adj[i] = vector<int>();
}
 
// Function to add edge
// in the graph
void Graph::addEdge(int v, int w)
{
  adj[v].push_back(w);
  adj[w].push_back(v);
}
 
// Function to perform DFS
void Graph::DFS(int s, vector<bool> &visited)
{
   
  // Create a stack for DFS
  stack<int> stack;
 
  // Push the current source node
  stack.push(s);
  while (!stack.empty())
  {
     
    // Pop a vertex from stack
    // and print it
    s = stack.top();
    stack.pop();
 
    // Traverse adjacent vertices
    // of the popped vertex s
    for(auto node : adj[s])
    {
      if (!visited[node])
      {
         
        // If adjacent is unvisited,
        // push it to the stack
        visited[node] = true;
        stack.push(node);
      }
    }
  }
}
 
// Function to return the count
// edges removed
void countRemovedEdges(int N, int M, int K)
{
  int C = 0;
 
  // Initially mark all verices
  // as not visited
  vector<bool> visited(g->V + 1, false);
 
  for(int node = 1; node <= N; node++)
  {
     
    // If node is unvisited
    if (!visited[node])
    {
       
      // Increment Connected
      // component count by 1
      C = C + 1;
 
      // Perform DFS Traversal
      g->DFS(node, visited);
 
      // Print the result
      if (C <= K)
        cout << M - N + K << endl;
      else
        cout << -1 << endl;
    }
  }
}
 
// Driver Code
int main(int argc, char const *argv[])
{
  int N = 4, M = 3, K = 2;
 
  // Create Graph
  g = new Graph(N);
 
  // Given Edges
  g->addEdge(1, 2);
  g->addEdge(2, 3);
  g->addEdge(3, 4);
 
  // Function Call
  countRemovedEdges(N, M, K);
}
 
// This code is contributed by sanjeev2552

Java

// Java program to implement 
// the above approach
import java.util.*;
class GFG
{
 
  static ArrayList<ArrayList<Integer>> graph;
 
  // Function to perform DFS
  static void DFS(int s, boolean[] visited)
  {
 
    // Create a stack for DFS
    Stack<Integer> stack = new Stack<>();
 
    // Push the current source node
    stack.push(s);
    while (!stack.isEmpty())
    {
 
      // Pop a vertex from stack
      // and print it
      s = stack.peek();
      stack.pop();
 
      // Traverse adjacent vertices
      // of the popped vertex s
      for(Integer node : graph.get(s))
      {
        if (!visited[node])
        {
 
          // If adjacent is unvisited,
          // push it to the stack
          visited[node] = true;
          stack.push(node);
        }
      }
    }
  }
 
  // Function to return the count
  // edges removed
  static void countRemovedEdges(int N, int M, int K)
  {
    int C = 0;
 
    // Initially mark all verices
    // as not visited
    boolean[] visited = new boolean[N+1];
 
    for(int node = 1; node <= N; node++)
    {
 
      // If node is unvisited
      if (!visited[node])
      {
 
        // Increment Connected
        // component count by 1
        C = C + 1;
 
        // Perform DFS Traversal
        DFS(node, visited);
 
        // Print the result
        if (C <= K)
          System.out.println(M - N + K);
        else
          System.out.println(-1);
      }
    }
  }
 
  // Driver code
  public static void main (String[] args)
  {
    int N = 4, M = 3, K = 2;
 
    // Create Graph
    graph = new ArrayList<>();
 
    for(int i = 0; i <= N; i++)
      graph.add(new ArrayList<Integer>());
 
    // Given Edges
    graph.get(1).add(2);
    graph.get(2).add(3);
    graph.get(3).add(4);
 
    // Function Call
    countRemovedEdges(N, M, K);
  }
}
 
// This code is contributed by offbeat.

Python3

# Python3 program for the above approach
 
class Graph:
 
    # Constructor
    def __init__(self, V):
 
        # No. of vertices
        self.V = V
 
        # Dictionary of lists
        self.adj = {i: [] for i in range(1, V + 1)}
 
    # Function to add edge
    # in the graph
    def addEdge(self, v, w):
        self.adj[v].append(w)
        self.adj[w].append(v)
 
    # Function to perform DFS
    def DFS(self, s, visited):
 
    # Create a stack for DFS
        stack = []
 
        # Push the current source node
        stack.append(s)
        while (len(stack)):
 
            # Pop a vertex from stack
            # and print it
            s = stack[-1]
            stack.pop()
 
            # Traverse adjacent vertices
            # of the popped vertex s
            for node in self.adj[s]:
                if (not visited[node]):
 
                    # If adjacent is unvisited,
                    # push it to the stack
                    visited[node] = True
                    stack.append(node)
 
# Function to return the count
# edges removed
def countRemovedEdges(N, M, K):
 
    C = 0
 
    # Initially mark all verices
    # as not visited
    visited = [False for i in range(g.V + 1)]
 
    for node in range(1, N + 1):
 
        # If node is unvisited
        if (not visited[node]):
 
            # Increment Connected
            # component count by 1
            C = C + 1
 
            # Perform DFS Traversal
            g.DFS(node, visited)
 
    # Print the result
    if C <= K:
        print(M - N + K)
    else:
        print(-1)
 
 
# Driver Code
 
N, M, K = 4, 3, 2
 
# Create Graph
g = Graph(N)
 
# Given Edges
g.addEdge(1, 2)
g.addEdge(2, 3)
g.addEdge(3, 4)
 
# Function Call
countRemovedEdges(N, M, K)

Output:

Time Complexity: O(N + M)
Auxiliary Space: O(M + N)

Attention reader! Don’t stop learning now. Get hold of all the important DSA concepts with the DSA Self Paced Course at a student-friendly price and become industry ready. To complete your preparation from learning a language to DS Algo and many more, please refer Complete Interview Preparation Course.

In case you wish to attend live classes with industry experts, please refer Geeks Classes Live

My Personal Notes

Related Articles

C++

Java

Python3