Maximum number of edges in Bipartite graph

Given an integer N which represents the number of Vertices. The Task is to find the maximum number of edges possible in a Bipartite graph of N vertices.
Bipartite Graph:

1. A Bipartite graph is one which is having 2 sets of vertices.
2. The set are such that the vertices in the same set will never share an edge between them.

Examples:

Input: N = 10 
Output: 25 
Both the sets will contain 5 vertices and every vertex of first set 
will have an edge to every other vertex of the second set 
i.e. total edges = 5 * 5 = 25
Input: N = 9 
Output: 20 

Approach: The number of edges will be maximum when every vertex of a given set has an edge to every other vertex of the other set i.e. edges = m * n where m and n are the number of edges in both the sets. in order to maximize the number of edges, m must be equal to or as close to n as possible. Hence, the maximum number of edges can be calculated with the formula, 

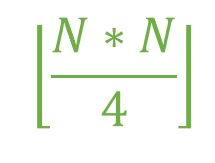
Below is the implementation of the above approach: 

C++

// C++ implementation of the approach
#include <bits/stdc++.h>
using namespace std;

// Function to return the maximum number
// of edges possible in a Bipartite
// graph with N vertices
int maxEdges(int N)
{
    int edges = 0;

    edges = floor((N * N) / 4);

    return edges;
}

// Driver code
int main()
{
    int N = 5;
    cout << maxEdges(N);

    return 0;
}

Java

// Java implementation of the approach

class GFG {

    // Function to return the maximum number
    // of edges possible in a Bipartite
    // graph with N vertices
    public static double maxEdges(double N)
    {
        double edges = 0;

        edges = Math.floor((N * N) / 4);

        return edges;
    }

    // Driver code
    public static void main(String[] args)
    {
        double N = 5;
        System.out.println(maxEdges(N));
    }
}

// This code is contributed by Naman_Garg.

Python3

# Python3 implementation of the approach

# Function to return the maximum number
# of edges possible in a Bipartite
# graph with N vertices
def maxEdges(N) :

    edges = 0;

    edges = (N * N) // 4;

    return edges;

# Driver code
if __name__ == "__main__" :

    N = 5;
    print(maxEdges(N));

# This code is contributed by AnkitRai01

C#

// C# implementation of the approach
using System;

class GFG {

    // Function to return the maximum number
    // of edges possible in a Bipartite
    // graph with N vertices
    static double maxEdges(double N)
    {
        double edges = 0;

        edges = Math.Floor((N * N) / 4);

        return edges;
    }

    // Driver code
    static public void Main()
    {
        double N = 5;
        Console.WriteLine(maxEdges(N));
    }
}

// This code is contributed by jit_t.

PHP

<?php
// PHP implementation of the approach

// Function to return the maximum number
// of edges possible in a Bipartite
// graph with N vertices

function maxEdges($N)
{
    $edges = 0;

    $edges = floor(($N * $N) / 4);

    return $edges;
}

// Driver code
    $N = 5;
    echo maxEdges($N);

// This code is contributed by ajit.
?>

Javascript

<script>

// Javascript implementation of the approach

// Function to return the maximum number
// of edges possible in a Bipartite
// graph with N vertices
function maxEdges(N)
{
    var edges = 0;

    edges = Math.floor((N * N) / 4);

    return edges;
}

// Driver code
var N = 5;
document.write( maxEdges(N));

</script>

Output:

6

Time Complexity: O(1)

Auxiliary Space: O(1)