Maximum distinct lines passing through a single point
Last Updated :
28 Jul, 2022
Given 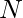 lines represented by two points
lines represented by two points 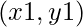 and
and 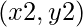 . The task is to find maximum number of lines which can pass through a single point, without superimposing (or covering) any other line. We can move any line but not rotate it.
. The task is to find maximum number of lines which can pass through a single point, without superimposing (or covering) any other line. We can move any line but not rotate it.
Examples:
Input : Line 1 : x1 = 1, y1 = 1, x2 = 2, y2 = 2
Line 2 : x2 = 2, y1 = 2, x2 = 4, y2 = 10
Output : 2
There are two lines. These two lines are not
parallel, so both of them will pass through
a single point.
Input : Line 1 : x1 = 1, y1 = 5, x2 = 1, y2 = 10
Line 2 : x2 = 5, y1 = 1, x2 = 10, y2 = 1
Output : 2
- Represent lines as pair
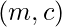 where line can be given as
where line can be given as 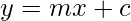 , called line slope form. We can now see that we can change the c for any line, but cannot modify m.
, called line slope form. We can now see that we can change the c for any line, but cannot modify m. - Lines having same value of m parallel, given that (c1 ? c2). Also no two parallel lines can pass through same point without superimposing to each other.
- So, our problem reduces to finding different values of slopes from given set of lines.
We can calculate slope of a line as 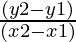 , add them to a set and count the number of distinct values of slope in set. But we have to handle vertical lines separately.
, add them to a set and count the number of distinct values of slope in set. But we have to handle vertical lines separately.
So, if 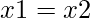 then, slope = INT_MAX.
then, slope = INT_MAX.
Otherwise, slope = 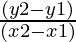 .
.
Below is the implementation of the approach.
C++
#include <bits/stdc++.h>
using namespace std;
int maxLines(int n, int x1[], int y1[],
int x2[], int y2[])
{
unordered_set<double> s;
double slope;
for (int i = 0; i < n; ++i) {
if (x1[i] == x2[i])
slope = INT_MAX;
else
slope = (y2[i] - y1[i]) * 1.0
/ (x2[i] - x1[i]) * 1.0;
s.insert(slope);
}
return s.size();
}
int main()
{
int n = 2, x1[] = { 1, 2 }, y1[] = { 1, 2 },
x2[] = { 2, 4 }, y2[] = { 2, 10 };
cout << maxLines(n, x1, y1, x2, y2);
return 0;
}
|
Java
import java.util.*;
import java.lang.*;
import java.io.*;
class GFG{
static int maxLines(int n, int x1[], int y1[],
int x2[], int y2[])
{
Set<Double> s=new HashSet<Double>();
double slope;
for (int i = 0; i < n; ++i) {
if (x1[i] == x2[i])
slope = Integer.MAX_VALUE;
else
slope = (y2[i] - y1[i]) * 1.0
/ (x2[i] - x1[i]) * 1.0;
s.add(slope);
}
return s.size();
}
public static void main(String args[])
{
int n = 2, x1[] = { 1, 2 }, y1[] = { 1, 2 },
x2[] = { 2, 4 }, y2[] = { 2, 10 };
System.out.print(maxLines(n, x1, y1, x2, y2));
}
}
|
Python3
import sys
def maxLines(n, x1, y1, x2, y2):
s = [];
slope=sys.maxsize;
for i in range(n):
if (x1[i] == x2[i]):
slope = sys.maxsize;
else:
slope = (y2[i] - y1[i]) * 1.0 /(x2[i] - x1[i]) * 1.0;
s.append(slope);
return len(s);
n = 2;
x1 = [ 1, 2 ];
y1 = [1, 2];
x2 = [2, 4];
y2 = [2, 10];
print(maxLines(n, x1, y1, x2, y2));
|
C#
using System;
using System.Collections.Generic;
class GFG
{
static int maxLines(int n, int []x1, int []y1,
int []x2, int []y2)
{
HashSet<Double> s = new HashSet<Double>();
double slope;
for (int i = 0; i < n; ++i)
{
if (x1[i] == x2[i])
slope = int.MaxValue;
else
slope = (y2[i] - y1[i]) * 1.0
/ (x2[i] - x1[i]) * 1.0;
s.Add(slope);
}
return s.Count;
}
public static void Main()
{
int n = 2;
int []x1 = { 1, 2 }; int []y1 = { 1, 2 };
int []x2 = { 2, 4 }; int []y2 = { 2, 10 };
Console.Write(maxLines(n, x1, y1, x2, y2));
}
}
|
PHP
<?php
function maxLines($n, $x1, $y1, $x2, $y2)
{
$s = array();
$slope;
for ($i = 0; $i < $n; ++$i)
{
if ($x1[$i] == $x2[$i])
$slope = PHP_INT_MAX;
else
$slope = ($y2[$i] - $y1[$i]) * 1.0 /
($x2[$i] - $x1[$i]) * 1.0;
array_push($s, $slope);
}
return count($s);
}
$n = 2;
$x1 = array( 1, 2 );
$y1 = array(1, 2);
$x2 = array(2, 4);
$y2 = array(2, 10);
echo maxLines($n, $x1, $y1, $x2, $y2);
?>
|
Javascript
<script>
function maxLines(n, x1, y1, x2, y2) {
var s = [];
var slope = 2147483647;
for (let i = 0; i < n; i++) {
if (x1[i] === x2[i]) slope = 2147483647;
else slope = (((y2[i] - y1[i]) * 1.0) / (x2[i] - x1[i])) * 1.0;
s.push(slope);
}
return s.length;
}
var n = 2;
var x1 = [1, 2];
var y1 = [1, 2];
var x2 = [2, 4];
var y2 = [2, 10];
document.write(maxLines(n, x1, y1, x2, y2));
</script>
|
Time Complexity: 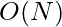
Space Complexity: O(N) since using auxiliary space for set
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...