Maximum circular subarray sum of size K
Last Updated :
23 Dec, 2022
Given an array arr of size N and an integer K, the task is to find the maximum sum subarray of size k among all contiguous sub-array (considering circular subarray also).
Examples:
Input: arr = {18, 4, 3, 4, 5, 6, 7, 8, 2, 10}, k = 3
Output:
max circular sum = 32
start index = 9
end index = 1
Explanation:
Maximum Sum = 10 + 18 + 4 = 32
Input: arr = {8, 2, 5, 9}, k = 4
Output:
max circular sum = 24
start index = 0
end index = 3
Approach:
- Iterate the loop till (n + k) times and
- Take (i % n) to handle the case when the array index becomes greater than n.
Below is the implementation of above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void maxCircularSum(int arr[], int n, int k)
{
if (n < k) {
cout << "Invalid";
return;
}
int sum = 0, start = 0, end = k - 1;
for (int i = 0; i < k; i++) {
sum += arr[i];
}
int ans = sum;
for (int i = k; i < n + k; i++) {
sum += arr[i % n] - arr[(i - k) % n];
if (sum > ans) {
ans = sum;
start = (i - k + 1) % n;
end = i % n;
}
}
cout << "max circular sum = "
<< ans << endl;
cout << "start index = " << start
<< "\nend index = " << end << endl;
}
int main()
{
int arr[] = { 18, 4, 3, 4, 5, 6, 7, 8, 2, 10 };
int n = sizeof(arr) / sizeof(arr[0]);
int k = 3;
maxCircularSum(arr, n, k);
return 0;
}
|
Java
import java.util.*;
class GFG
{
static void maxCircularSum(int[] arr, int n, int k)
{
if (n < k)
{
System.out.println("Invalid");
return;
}
int sum = 0, start = 0, end = k - 1;
for (int i = 0; i < k; i++)
sum += arr[i];
int ans = sum;
for (int i = k; i < n + k; i++)
{
sum += arr[i % n] - arr[(i - k) % n];
if (sum > ans)
{
ans = sum;
start = (i - k + 1) % n;
end = i % n;
}
}
System.out.println("max circular sum = " + ans);
System.out.println("start index = " + start + "\nend index = " + end);
}
public static void main(String[] args)
{
int[] arr = { 18, 4, 3, 4, 5, 6, 7, 8, 2, 10 };
int n = arr.length;
int k = 3;
maxCircularSum(arr, n, k);
}
}
|
Python3
def maxCircularSum(arr, n, k) :
if (n < k) :
print("Invalid");
return;
sum = 0; start = 0; end = k - 1;
for i in range(k) :
sum += arr[i];
ans = sum;
for i in range(k, n + k) :
sum += arr[i % n] - arr[(i - k) % n];
if (sum > ans) :
ans = sum;
start = (i - k + 1) % n;
end = i % n;
print("max circular sum = ",ans);
print("start index = ", start,
"\nend index = ", end);
if __name__ == "__main__" :
arr = [ 18, 4, 3, 4, 5, 6, 7, 8, 2, 10 ];
n = len(arr);
k = 3;
maxCircularSum(arr, n, k);
|
C#
using System;
class GFG
{
static void maxCircularSum(int[] arr,
int n, int k)
{
if (n < k)
{
Console.WriteLine("Invalid");
return;
}
int sum = 0, start = 0, end = k - 1;
for (int i = 0; i < k; i++)
sum += arr[i];
int ans = sum;
for (int i = k; i < n + k; i++)
{
sum += arr[i % n] - arr[(i - k) % n];
if (sum > ans)
{
ans = sum;
start = (i - k + 1) % n;
end = i % n;
}
}
Console.WriteLine("max circular sum = " + ans);
Console.WriteLine("start index = " + start +
"\nend index = " + end);
}
public static void Main(String[] args)
{
int[] arr = { 18, 4, 3, 4, 5,
6, 7, 8, 2, 10 };
int n = arr.Length;
int k = 3;
maxCircularSum(arr, n, k);
}
}
|
Javascript
<script>
function maxCircularSum(arr, n, k)
{
if (n < k)
{
document.write("Invalid");
return;
}
let sum = 0, start = 0, end = k - 1;
for(let i = 0; i < k; i++)
{
sum += arr[i];
}
let ans = sum;
for(let i = k; i < n + k; i++)
{
sum += arr[i % n] - arr[(i - k) % n];
if (sum > ans)
{
ans = sum;
start = (i - k + 1) % n;
end = i % n;
}
}
document.write("max circular sum = " +
ans + "<br>");
document.write("start index = " + start +
"<br>end index = " + end +
"<br>");
}
let arr = [ 18, 4, 3, 4, 5,
6, 7, 8, 2, 10 ];
let n = arr.length
let k = 3;
maxCircularSum(arr, n, k);
</script>
|
Output: max circular sum = 32
start index = 9
end index = 1
Time Complexity: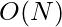
Auxiliary Space: O(1), no extra space is required, so it is a constant.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...