Maximum area of quadrilateral
Last Updated :
22 Jun, 2022
Given four sides of quadrilateral a, b, c, d, find the maximum area of the quadrilateral possible from the given sides .
Examples:
Input : 1 2 1 2
Output : 2.00
It is optimal to construct a rectangle for maximum area .
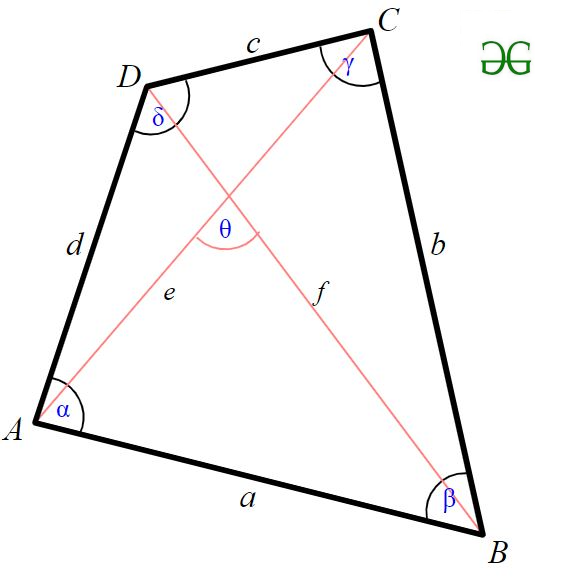
According to Bretschneider’s formula, the area of a general quadrilateral is given by 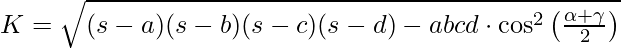
Here a, b, c, d are the sides of a quadrilateral, s is the semiperimeter of a quadrilateral and angles are two opposite angles.
So, this formula is maximized only when opposite angles sum to pi(180) then we can use a simplified form of Bretschneider’s formula to get the (maximum) area K.
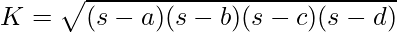
This formula is called as Brahmagupta’s formula .
Below is the implementation of given approach
C++
#include <iostream>
#include <math.h>
using namespace std;
double maxArea(double a, double b,
double c, double d)
{
double semiperimeter = (a + b + c + d) / 2;
return sqrt((semiperimeter - a) *
(semiperimeter - b) *
(semiperimeter - c) *
(semiperimeter - d));
}
int main()
{
double a = 1, b = 2, c= 1, d = 2;
cout <<maxArea(a, b, c, d);
return 0;
}
|
C
#include <stdio.h>
#include <math.h>
double maxArea(double a, double b,
double c, double d)
{
double semiperimeter = (a + b + c + d) / 2;
return sqrt((semiperimeter - a) *
(semiperimeter - b) *
(semiperimeter - c) *
(semiperimeter - d));
}
int main()
{
double a = 1, b = 2, c= 1, d = 2;
printf("%.2f\n",maxArea(a, b, c, d));
return 0;
}
|
Java
import java.io.*;
class GFG
{
static double maxArea(double a, double b,
double c, double d)
{
double semiperimeter = (a + b + c + d) / 2;
return Math.sqrt((semiperimeter - a) *
(semiperimeter - b) *
(semiperimeter - c) *
(semiperimeter - d));
}
public static void main (String[] args)
{
double a = 1, b = 2, c= 1, d = 2;
System.out.println(maxArea(a, b, c, d));
}
}
|
Python3
import math
def maxArea (a , b , c , d ):
semiperimeter = (a + b + c + d) / 2
return math.sqrt((semiperimeter - a) *
(semiperimeter - b) *
(semiperimeter - c) *
(semiperimeter - d))
a = 1
b = 2
c = 1
d = 2
print("%.2f"%maxArea(a, b, c, d))
|
C#
using System;
class GFG {
static double maxArea(double a, double b,
double c, double d)
{
double semiperimeter = (a + b + c + d) / 2;
return Math.Sqrt((semiperimeter - a) *
(semiperimeter - b) *
(semiperimeter - c) *
(semiperimeter - d));
}
public static void Main ()
{
double a = 1, b = 2, c= 1, d = 2;
Console.WriteLine(maxArea(a, b, c, d));
}
}
|
PHP
<?php
function maxArea( $a, $b, $c, $d)
{
$semiperimeter = ($a + $b + $c + $d) / 2;
return sqrt(($semiperimeter - $a) *
($semiperimeter - $b) *
($semiperimeter - $c) *
($semiperimeter - $d));
}
$a = 1; $b = 2; $c= 1; $d = 2;
echo(maxArea($a, $b, $c, $d));
?>
|
Javascript
<script>
function maxArea(a, b, c, d)
{
let semiperimeter = (a + b + c + d) / 2;
return Math.sqrt((semiperimeter - a) *
(semiperimeter - b) *
(semiperimeter - c) *
(semiperimeter - d));
}
let a = 1, b = 2, c= 1, d = 2;
document.write(maxArea(a, b, c, d));
</script>
|
Output:
2.00
Time Complexity: O(logn)
Auxiliary Space: O(1)
Please suggest if someone has a better solution which is more efficient in terms of space and time.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...