Maximum area of rectangle inscribed in an equilateral triangle
Last Updated :
18 Sep, 2022
Given an integer A, which denotes the side of an equilateral triangle, the task is to find the maximum area of the rectangle that can be inscribed in the triangle.
Examples:
Input: A = 10
Output: 21.65
Explanation:
Maximum area of rectangle inscribed in an equilateral triangle of side 10 is 21.65.
Input: A = 12
Output: 31.176
Explanation:
Maximum area of rectangle inscribed in an equilateral triangle of side 12 is 31.176.
Approach: The idea is to use the fact that interior angles of an equilateral triangle is 60o. Then, Draw the perpendicular from one of the side of the triangle and compute the sides of the rectangle with the help of below formulae
The length of Rectangle = (Side of Equilateral Triangle)/2
The breadth of Rectangle = sqrt(3) * (Side of Equilateral Triangle)/4
Then, Maximum area of the rectangle will be 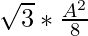
Below is the implementation of the above approach:
C++
#include<bits/stdc++.h>
using namespace std;
double solve(int s)
{
double area = (1.732 * pow(s, 2))/8;
return area;
}
int main()
{
int n = 14;
cout << solve(n);
}
|
Java
class GFG
{
static double solve(int s)
{
double area = (1.732 * Math.pow(s, 2))/8;
return area;
}
public static void main(String[] args)
{
int n = 14;
System.out.println(solve(n));
}
}
|
Python3
def solve(s):
area = (1.732 * s**2)/8
return area
if __name__=='__main__':
n = 14
print(solve(n))
|
C#
using System;
class GFG
{
static double solve(int s)
{
double area = (1.732 * Math.Pow(s, 2))/8;
return area;
}
public static void Main(String[] args)
{
int n = 14;
Console.WriteLine(solve(n));
}
}
|
Javascript
<script>
function solve(s)
{
let area = (1.732 * Math.pow(s, 2))/8;
return area;
}
let n = 14;
document.write(solve(n));
</script>
|
Time complexity: O(1) as constant operations are done
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...