Maximum absolute difference of value and index sums

Given an unsorted array A of N integers, 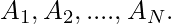Return maximum value of f(i, j) for all 1 ? i, j ? N.
f(i, j) or absolute difference of two elements of an array A is defined as |A[i] – A[j]| + |i – j|, where |A| denotes the absolute value of A.

Examples:

We will calculate the value of f(i, j) for each pair
of (i, j) and return the maximum value thus obtained.

Input : A = {1, 3, -1}
Output : 5
f(1, 1) = f(2, 2) = f(3, 3) = 0
f(1, 2) = f(2, 1) = |1 - 3| + |1 - 2| = 3
f(1, 3) = f(3, 1) = |1 - (-1)| + |1 - 3| = 4
f(2, 3) = f(3, 2) = |3 - (-1)| + |2 - 3| = 5
So, we return 5.

Input : A = {3, -2, 5, -4}
Output : 10
f(1, 1) = f(2, 2) = f(3, 3) = f(4, 4) = 0
f(1, 2) = f(2, 1) = |3 - (-2)| + |1 - 2| = 6
f(1, 3) = f(3, 1) = |3 - 5| + |1 - 3| = 4
f(1, 4) = f(4, 1) = |3 - (-4)| + |1 - 4| = 10
f(2, 3) = f(3, 2) = |(-2) - 5| + |2 - 3| = 8
f(2, 4) = f(4, 2) = |(-2) - (-4)| + |2 - 4| = 4
f(3, 4) = f(4, 3) = |5 - (-4)| + |3 - 4| = 10

So, we return 10

A naive brute force approach is to calculate the value f(i, j) by iterating over all such pairs (i, j) and calculating the maximum absolute difference which is implemented below.

Implementation:

C++

// Brute force C++ program to calculate the
// maximum absolute difference of an array.
#include <bits/stdc++.h>
using namespace std;

int calculateDiff(int i, int j, int arr[])
{
    // Utility function to calculate
    // the value of absolute difference
    // for the pair (i, j).
    return abs(arr[i] - arr[j]) + abs(i - j);
}

// Function to return maximum absolute
// difference in brute force.
int maxDistance(int arr[], int n)
{
    // Variable for storing the maximum
    // absolute distance throughout the
    // traversal of loops.
    int result = 0;

    // Iterate through all pairs.
    for (int i = 0; i < n; i++) {
        for (int j = i; j < n; j++) {

            // If the absolute difference of
            // current pair (i, j) is greater
            // than the maximum difference
            // calculated till now, update
            // the value of result.
            if (calculateDiff(i, j, arr) > result)
                result = calculateDiff(i, j, arr);
        }
    }
    return result;
}

// Driver program to test the above function.
int main()
{
    int arr[] = { -70, -64, -6, -56, 64,
                  61, -57, 16, 48, -98 };

    int n = sizeof(arr) / sizeof(arr[0]);

    cout << maxDistance(arr, n) << endl;

    return 0;
}

Java

// Java program to calculate the maximum
// absolute difference of an array.
public class MaximumAbsoluteDifference
{
    private static int calculateDiff(int i, int j,
                                     int[] array)
    {
        // Utility function to calculate
        // the value of absolute difference
        // for the pair (i, j).
        return Math.abs(array[i] - array[j]) +
                            Math.abs(i - j);
    }

    // Function to return maximum absolute
    // difference in brute force.
    private static int maxDistance(int[] array)
    {
        // Variable for storing the maximum
        // absolute distance throughout the
        // traversal of loops.
        int result = 0;

        // Iterate through all pairs.
        for (int i = 0; i < array.length; i++)
        {
            for (int j = i; j < array.length; j++)
            {

                // If the absolute difference of
                // current pair (i, j) is greater
                // than the maximum difference
                // calculated till now, update
                // the value of result.
                result = Math.max(result, calculateDiff(i, j, array));
            }
        }
        return result;
    }

    // Driver program to test above function
    public static void main(String[] args)
    {
        int[] array = { -70, -64, -6, -56, 64,
                        61, -57, 16, 48, -98 };
        System.out.println(maxDistance(array));
    }
}

// This code is contributed by Harikrishnan Rajan

Python3

# Brute force Python 3 program
# to calculate the maximum
# absolute difference of an array.

def calculateDiff(i, j, arr):

    # Utility function to calculate
    # the value of absolute difference
    # for the pair (i, j).
    return abs(arr[i] - arr[j]) + abs(i - j)

# Function to return maximum
# absolute difference in
# brute force.
def maxDistance(arr, n):

    # Variable for storing the
    # maximum absolute distance
    # throughout the traversal
    # of loops.
    result = 0

    # Iterate through all pairs.
    for i in range(0,n):
        for j in range(i, n):

            # If the absolute difference of
            # current pair (i, j) is greater
            # than the maximum difference
            # calculated till now, update
            # the value of result.
            if (calculateDiff(i, j, arr) > result):
                result = calculateDiff(i, j, arr)

    return result

# Driver program
arr = [ -70, -64, -6, -56, 64,
         61, -57, 16, 48, -98 ]
n = len(arr)

print(maxDistance(arr, n))

# This code is contributed by Smitha Dinesh Semwal

C#

// C# program to calculate the maximum
// absolute difference of an array.
using System;

public class MaximumAbsoluteDifference
{
    private static int calculateDiff(int i, int j,
                                    int[] array)
    {
        // Utility function to calculate
        // the value of absolute difference
        // for the pair (i, j).
        return Math.Abs(array[i] - array[j]) +
                            Math.Abs(i - j);
    }

    // Function to return maximum absolute
    // difference in brute force.
    private static int maxDistance(int[] array)
    {
        // Variable for storing the maximum
        // absolute distance throughout the
        // traversal of loops.
        int result = 0;

        // Iterate through all pairs.
        for (int i = 0; i < array.Length; i++)
        {
            for (int j = i; j < array.Length; j++)
            {

                // If the absolute difference of
                // current pair (i, j) is greater
                // than the maximum difference
                // calculated till now, update
                // the value of result.
                result = Math.Max(result, calculateDiff(i, j, array));
            }
        }
        return result;
    }

    // Driver program
    public static void Main()
    {
        int[] array = { -70, -64, -6, -56, 64,
                        61, -57, 16, 48, -98 };
        Console.WriteLine(maxDistance(array));
    }
}

// This code is contributed by vt_m

PHP

<?php
// Brute force PHP program to
// calculate the maximum absolute
// difference of an array.

function calculateDiff($i, $j, $arr)
{
    // Utility function to calculate
    // the value of absolute difference
    // for the pair (i, j).
    return abs($arr[$i] - $arr[$j]) +
           abs($i - $j);
}

// Function to return maximum
// absolute difference in brute force.
function maxDistance($arr, $n)
{
    // Variable for storing the maximum
    // absolute distance throughout the
    // traversal of loops.
    $result = 0;

    // Iterate through all pairs.
    for ($i = 0; $i < $n; $i++)
    {
        for ($j = $i; $j < $n; $j++)
        {

            // If the absolute difference of
            // current pair (i, j) is greater
            // than the maximum difference
            // calculated till now, update
            // the value of result.
            if (calculateDiff($i, $j, $arr) > $result)
                $result = calculateDiff($i, $j, $arr);
        }
    }
    return $result;
}

// Driver Code
$arr = array( -70, -64, -6, -56, 64,
               61, -57, 16, 48, -98 );

$n = sizeof($arr);

echo maxDistance($arr, $n);

// This Code is contributed by mits
?>

Javascript

<script>

// javascript program to calculate the maximum
// absolute difference of an array.

let MAX = 256;

    // Function to count the number of equal pairs
    function calculateDiff(i, j, array)
    {
        // Utility function to calculate
        // the value of absolute difference
        // for the pair (i, j).
        return Math.abs(array[i] - array[j]) +
                            Math.abs(i - j);
    }

    // Function to return maximum absolute
    // difference in brute force.
    function maxDistance(array)
    {
        // Variable for storing the maximum
        // absolute distance throughout the
        // traversal of loops.
        let result = 0;

        // Iterate through all pairs.
        for (let i = 0; i < array.length; i++)
        {
            for (let j = i; j < array.length; j++)
            {

                // If the absolute difference of
                // current pair (i, j) is greater
                // than the maximum difference
                // calculated till now, update
                // the value of result.
                result = Math.max(result, calculateDiff(i, j, array));
            }
        }
        return result;
    }

// Driver Function
        let array = [-70, -64, -6, -56, 64,
                        61, -57, 16, 48, -98 ];
        document.write(maxDistance(array));

    // This code is contributed by susmitakundugoaldanga.
</script>

Output

167

Time complexity: O(n²)
Auxiliary Space: O(1)

An efficient solution in O(n) time complexity can be worked out using the properties of absolute values. 
f(i, j) = |A[i] – A[j]| + |i – j| can be written in 4 ways (Since we are looking at max value, we don’t even care if the value becomes negative as long as we are also covering the max value in some way). 

Case 1: A[i] > A[j] and i > j
|A[i] - A[j]| = A[i] - A[j]
|i -j| = i - j
hence, f(i, j) = (A[i] + i) - (A[j] + j)

Case 2: A[i] < A[j] and i < j
|A[i] - A[j]| = -(A[i]) + A[j]
|i -j| = -(i) + j
hence, f(i, j) = -(A[i] + i) + (A[j] + j)

Case 3: A[i] > A[j] and i < j
|A[i] - A[j]| = A[i] - A[j]
|i -j| = -(i) + j
hence, f(i, j) = (A[i] - i) - (A[j] - j)

Case 4: A[i] < A[j] and i > j
|A[i] - A[j]| = -(A[i]) + A[j]
|i -j| = i - j
hence, f(i, j) = -(A[i] - i) + (A[j] - j)

Note that cases 1 and 2 are equivalent and so are cases 3 and 4 and hence we can design our algorithm only for two cases as it will cover all the possible cases.

1. Calculate the value of A[i] + i and A[i] – i for every element of the array while traversing through the array.
2. Then for the two equivalent cases, we find the maximum possible value. For that, we have to store minimum and maximum values of expressions A[i] + i and A[i] – i for all i.
3. Hence the required maximum absolute difference is maximum of two values i.e. max((A[i] + i) – (A[j] + j)) and max((A[i] – i) – (A[j] – j)). These values can be found easily in linear time. 
     a. For max((A[i] + i) – (A[j] + j)) Maintain two variables max1 and min1 which will store maximum and minimum values of A[i] + i respectively. max((A[i] + i) – (A[j] + j)) = max1 – min1 
     b. For max((A[i] – i) – (A[j] – j)). Maintain two variables max2 and min2 which will store maximum and minimum values of A[i] – i respectively. max((A[i] – i) – (A[j] – j)) = max2 – min2

Implementation using the above fast algorithm is given below. 

C++

// C++ program to calculate the maximum
// absolute difference of an array.
#include <bits/stdc++.h>
using namespace std;

// Function to return maximum absolute
// difference in linear time.
int maxDistance(int arr[], int n)
{
    // max and min variables as described
    // in algorithm.
    int max1 = INT_MIN, min1 = INT_MAX;
    int max2 = INT_MIN, min2 = INT_MAX;

    for (int i = 0; i < n; i++) {

        // Updating max and min variables
        // as described in algorithm.
        max1 = max(max1, arr[i] + i);
        min1 = min(min1, arr[i] + i);
        max2 = max(max2, arr[i] - i);
        min2 = min(min2, arr[i] - i);
    }

    // Calculating maximum absolute difference.
    return max(max1 - min1, max2 - min2);
}

// Driver program to test the above function.
int main()
{
    int arr[] = { -70, -64, -6, -56, 64,
                  61, -57, 16, 48, -98 };
    int n = sizeof(arr) / sizeof(arr[0]);
    cout << maxDistance(arr, n) << endl;
    return 0;
}

Java

// Java program to calculate the maximum
// absolute difference of an array.
public class MaximumAbsoluteDifference
{
    // Function to return maximum absolute
    // difference in linear time.
    private static int maxDistance(int[] array)
    {
        // max and min variables as described
        // in algorithm.
        int max1 = Integer.MIN_VALUE;
        int min1 = Integer.MAX_VALUE;
        int max2 = Integer.MIN_VALUE;
        int min2 = Integer.MAX_VALUE;

        for (int i = 0; i < array.length; i++)
        {

            // Updating max and min variables
            // as described in algorithm.
            max1 = Math.max(max1, array[i] + i);
            min1 = Math.min(min1, array[i] + i);
            max2 = Math.max(max2, array[i] - i);
            min2 = Math.min(min2, array[i] - i);
        }

        // Calculating maximum absolute difference.
        return Math.max(max1 - min1, max2 - min2);
    }

    // Driver program to test above function
    public static void main(String[] args)
    {
        int[] array = { -70, -64, -6, -56, 64,
                         61, -57, 16, 48, -98 };
        System.out.println(maxDistance(array));
    }
}

// This code is contributed by Harikrishnan Rajan

Python3

# Python program to
# calculate the maximum
# absolute difference
# of an array.

# Function to return
# maximum absolute
# difference in linear time.
def maxDistance(array):

    # max and min variables as described
    # in algorithm.
    max1 = -2147483648
    min1 = +2147483647
    max2 = -2147483648
    min2 = +2147483647

    for i in range(len(array)):


        # Updating max and min variables
        # as described in algorithm.
        max1 = max(max1, array[i] + i)
        min1 = min(min1, array[i] + i)
        max2 = max(max2, array[i] - i)
        min2 = min(min2, array[i] - i)


    # Calculating maximum absolute difference.
    return max(max1 - min1, max2 - min2)


# Driver program to
# test above function

array = [ -70, -64, -6, -56, 64,
           61, -57, 16, 48, -98 ]

print(maxDistance(array))

# This code is contributed
# by Anant Agarwal.

C#

// C# program to calculate the maximum
// absolute difference of an array.
using System;

public class MaximumAbsoluteDifference
{
    // Function to return maximum absolute
    // difference in linear time.
    private static int maxDistance(int[] array)
    {
        // max and min variables as described
        // in algorithm.
        int max1 = int.MinValue ;
        int min1 = int.MaxValue ;
        int max2 = int.MinValue ;
        int min2 =int.MaxValue ;

        for (int i = 0; i < array.Length; i++)
        {

            // Updating max and min variables
            // as described in algorithm.
            max1 = Math.Max(max1, array[i] + i);
            min1 = Math.Min(min1, array[i] + i);
            max2 = Math.Max(max2, array[i] - i);
            min2 = Math.Min(min2, array[i] - i);
        }

        // Calculating maximum absolute difference.
        return Math.Max(max1 - min1, max2 - min2);
    }

    // Driver program
    public static void Main()
    {
        int[] array = { -70, -64, -6, -56, 64,
                        61, -57, 16, 48, -98 };
        Console.WriteLine(maxDistance(array));
    }
}

// This code is contributed by vt_m

PHP

<?php
// PHP program to calculate the maximum
// absolute difference of an array.

// Function to return maximum absolute
// difference in linear time.
function maxDistance( $arr, $n)
{

    // max and min variables as
    // described in algorithm.
    $max1 = PHP_INT_MIN; $min1 =
                    PHP_INT_MAX;
    $max2 = PHP_INT_MIN;$min2 =
                    PHP_INT_MAX;

    for($i = 0; $i < $n; $i++)
    {

        // Updating max and min variables
        // as described in algorithm.
        $max1 = max($max1, $arr[$i] + $i);
        $min1 = min($min1, $arr[$i] + $i);
        $max2 = max($max2, $arr[$i] - $i);
        $min2 = min($min2, $arr[$i] - $i);
    }

    // Calculating maximum
    // absolute difference.
    return max($max1 - $min1,
               $max2 - $min2);
}

    // Driver Code
    $arr = array(-70, -64, -6, -56, 64,
                  61, -57, 16, 48, -98);
    $n = count($arr);
    echo maxDistance($arr, $n);

// This code is contributed by anuj_67.
?>

Javascript

<script>

    // JavaScript program to calculate the maximum
    // absolute difference of an array.

    // Function to return maximum absolute
    // difference in linear time.
    function maxDistance(array)
    {
        // max and min variables as described
        // in algorithm.
        let max1 = Number.MIN_VALUE;
        let min1 = Number.MAX_VALUE;
        let max2 = Number.MIN_VALUE;
        let min2 = Number.MAX_VALUE;

        for (let i = 0; i < array.length; i++)
        {

            // Updating max and min variables
            // as described in algorithm.
            max1 = Math.max(max1, array[i] + i);
            min1 = Math.min(min1, array[i] + i);
            max2 = Math.max(max2, array[i] - i);
            min2 = Math.min(min2, array[i] - i);
        }

        // Calculating maximum absolute difference.
        return Math.max(max1 - min1, max2 - min2);
    }

    let array =
    [ -70, -64, -6, -56, 64, 61, -57, 16, 48, -98 ];
    document.write(maxDistance(array));

</script>

Output

167

Time Complexity: O(n)
Auxiliary Space: O(1)