Maximize the length of upper boundary formed by placing given N rectangles horizontally or vertically
Last Updated :
06 Sep, 2021
Given a vector of pairs, V[] denoting the width and height of N rectangles numbered from 1 to N, these rectangles are placed in contact with the horizontal axis and are adjacent from left to right in numerical order. The task is to find the maximum length of the upper boundary formed by placing each of the rectangles either horizontally or vertically.
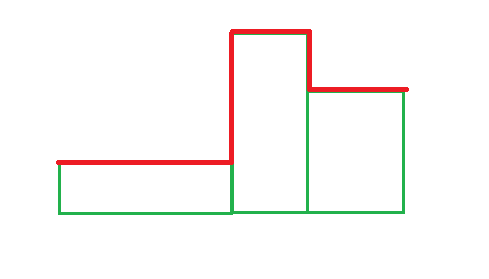
The red line shows the upper boundary of the figure
Examples:
Input: N = 5, V[] = {{2, 5}, {3, 8}, {1, 10}, {7, 14}, {2, 5}}
Output: 68
Explanation: Place the first and the third rectangle vertically and all the other rectangles horizontally to get the maximum length of the upper boundary. (5 + 6 + 3 + 7 + 10 + 13 + 7 + 12 + 5 = 68)
Input: N = 1, V[] = {{8, 7}}
Output: 8
Explanation: Place the only rectangle horizontally, so that the length of the upper boundary becomes 8.
Naive Approach: The simplest approach is to use recursion to try all possibilities by placing each rectangle either horizontally or vertically. For each rectangle, there are two choices either to place the current rectangle horizontally or to place the current rectangle vertically. Print the maximum boundary length among all the possibilities.
Time Complexity: O(2N)
Auxiliary Space: O(1)
Efficient Approach: To optimize the above approach, the idea is to use dynamic programming since the problem has overlapping subproblems and optimal substructure property. Each of the transition states has 2 options:
- Place the rectangle of the current transition state horizontally
- Place the rectangle of the current transition state vertically
Now, suppose the rectangle is placed horizontally then it contributes its width in the upper boundary. Now for this rectangle, the previous state rectangle would have been either in the horizontal position or in the vertical position. Calculate the contribution of the left vertical edge of the current rectangle if the previous rectangle was in a horizontal position or in a vertical position by subtracting the edges of the two rectangles.
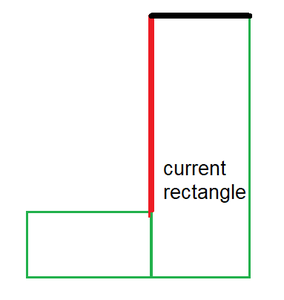
The red line shows the contribution of the current rectangle vertical edge and the black line shows the contribution of the current rectangle horizontal edge in the overall boundary.
Let’s define dp[i][0] as the maximum upper boundary of the first i rectangles if the ith rectangle is placed horizontally, and dp[i][1] as the maximum upper boundary of the first i rectangles if the ith rectangle is placed vertically. The transitions are defined as:
Let height1= |V[i – 1].second – V[i].second| and height2 = |V[i – 1].first – V[i].second|
Then, dp[i][0]= max(height1+dp[i-1][0], height2+dp[i-1][1])+V[i].first
Let vertical1 = |V[i].first – V[i -1].second| and vertical2 = | V[i].first – V[i – 1].first|
then dp[i][1] = max(vertical1 + dp[i-1][0], vertical2 + dp[i-1][1]) + V[i].second
Follow the steps below to solve the problem:
- Initialize a 2-D array dp[][] of size N*2. Initialize dp[0][0] = V[0].first and dp[0][1] = V[0].second.
- Traverse over the range [1, N] using the variable i and follow the below steps:
- Initialize variables height1 = absolute difference of V[i-1].second and V[i].second and height2 = absolute difference of V[i-1].first and V[i].second. Also update the value of dp[i][0] to V[i].first.
- Add max(dp[i-1][0]+height1, dp[i-1][1]+height2) to the value of dp[i][0].
- Initialize dp[i][1] to V[i].second. Also initialize variables vertical1 = absolute difference of V[i-1].first and V[i].first and vertical2 = absolute difference of V[i-1].first and V[i].first.
- Add max(dp[i-1][0]+vertical1, dp[i-1][1]+vertical2) to the value of dp[i][1].
- After completing the above steps print the value of max(dp[N-1][0], dp[N-1][1]).
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void maxBoundary(int N, vector<pair<int, int> > V)
{
int dp[N][2];
memset(dp, 0, sizeof(dp));
dp[0][0] = V[0].first;
dp[0][1] = V[0].second;
for (int i = 1; i < N; i++) {
dp[i][0] = V[i].first;
int height1 = abs(V[i - 1].second - V[i].second);
int height2 = abs(V[i - 1].first - V[i].second);
dp[i][0] += max(height1 + dp[i - 1][0],
height2 + dp[i - 1][1]);
dp[i][1] = V[i].second;
int vertical1 = abs(V[i].first - V[i - 1].second);
int vertical2 = abs(V[i].first - V[i - 1].first);
dp[i][1] += max(vertical1 + dp[i - 1][0],
vertical2 + dp[i - 1][1]);
}
cout << max(dp[N - 1][0], dp[N - 1][1]);
}
int main()
{
int N = 5;
vector<pair<int, int> > V
= { { 2, 5 }, { 3, 8 }, { 1, 10 }, { 7, 14 }, { 2, 5 } };
maxBoundary(N, V);
return 0;
}
|
Java
import java.util.Vector;
public class GFG {
public static class pair {
private int first;
private int second;
public pair(int first, int second)
{
this.first = first;
this.second = second;
}
}
static void maxBoundary(int N, Vector<pair> V)
{
int dp[][] = new int[N][2];
dp[0][0] = V.get(0).first;
dp[0][1] = V.get(0).second;
for (int i = 1; i < N; i++) {
dp[i][0] = V.get(i).first;
int height1 = Math.abs(V.get(i - 1).second
- V.get(i).second);
int height2 = Math.abs(V.get(i - 1).first
- V.get(i).second);
dp[i][0] += Math.max(height1 + dp[i - 1][0],
height2 + dp[i - 1][1]);
dp[i][1] = V.get(i).second;
int vertical1 = Math.abs(V.get(i).first
- V.get(i - 1).second);
int vertical2 = Math.abs(V.get(i).first
- V.get(i - 1).first);
dp[i][1] += Math.max(vertical1 + dp[i - 1][0],
vertical2 + dp[i - 1][1]);
}
System.out.println(
Math.max(dp[N - 1][0], dp[N - 1][1]));
}
public static void main(String[] args)
{
int N = 5;
Vector<pair> V = new Vector<>();
V.add(new pair(2, 5));
V.add(new pair(3, 8));
V.add(new pair(1, 10));
V.add(new pair(7, 14));
V.add(new pair(2, 5));
maxBoundary(N, V);
}
}
|
Python3
def maxBoundary(N, V):
dp = [[0 for i in range(2)] for j in range(N)]
dp[0][0] = V[0][0]
dp[0][1] = V[0][1]
for i in range(1, N, 1):
dp[i][0] = V[i][0]
height1 = abs(V[i - 1][1] - V[i][1])
height2 = abs(V[i - 1][0] - V[i][1])
dp[i][0] += max(height1 + dp[i - 1][0], height2 + dp[i - 1][1])
dp[i][1] = V[i][1]
vertical1 = abs(V[i][0] - V[i - 1][1]);
vertical2 = abs(V[i][0] - V[i - 1][1]);
dp[i][1] += max(vertical1 + dp[i - 1][0], vertical2 + dp[i - 1][1])
print(max(dp[N - 1][0], dp[N - 1][1])-1)
if __name__ == '__main__':
N = 5
V = [[2, 5],[3, 8],[1, 10],[7, 14],[2, 5]]
maxBoundary(N, V)
|
C#
using System;
using System.Collections.Generic;
class GFG {
static void maxBoundary(int N, List<Tuple<int,int>> V)
{
int[,] dp = new int[N,2];
dp[0,0] = V[0].Item1;
dp[0,1] = V[0].Item2;
for (int i = 1; i < N; i++) {
dp[i,0] = V[i].Item1;
int height1 = Math.Abs(V[i - 1].Item2
- V[i].Item2);
int height2 = Math.Abs(V[i - 1].Item1
- V[i].Item2);
dp[i,0] += Math.Max(height1 + dp[i - 1,0],
height2 + dp[i - 1,1]);
dp[i,1] = V[i].Item2;
int vertical1 = Math.Abs(V[i].Item1
- V[i - 1].Item2);
int vertical2 = Math.Abs(V[i].Item1
- V[i - 1].Item1);
dp[i,1] += Math.Max(vertical1 + dp[i - 1,0],
vertical2 + dp[i - 1,1]);
}
Console.WriteLine(Math.Max(dp[N - 1,0], dp[N - 1,1]));
}
static void Main()
{
int N = 5;
List<Tuple<int,int>> V = new List<Tuple<int,int>>();
V.Add(new Tuple<int,int>(2, 5));
V.Add(new Tuple<int,int>(3, 8));
V.Add(new Tuple<int,int>(1, 10));
V.Add(new Tuple<int,int>(7, 14));
V.Add(new Tuple<int,int>(2, 5));
maxBoundary(N, V);
}
}
|
Javascript
<script>
function maxBoundary(N, V)
{
let dp = new Array(N).fill(0).map(() => new Array(2).fill(0));
dp[0][0] = V[0][0];
dp[0][1] = V[0][1];
for (let i = 1; i < N; i++)
{
dp[i][0] = V[i][0];
let height1 = Math.abs(V[i - 1][1] - V[i][1]);
let height2 = Math.abs(V[i - 1][0] - V[i][1]);
dp[i][0] += Math.max(height1 + dp[i - 1][0], height2 + dp[i - 1][1]);
dp[i][1] = V[i][1];
let vertical1 = Math.abs(V[i][0] - V[i - 1][1]);
let vertical2 = Math.abs(V[i][0] - V[i - 1][0]);
dp[i][1] += Math.max(vertical1 + dp[i - 1][0], vertical2 + dp[i - 1][1]);
}
document.write(Math.max(dp[N - 1][0], dp[N - 1][1]));
}
let N = 5;
let V = [
[2, 5],
[3, 8],
[1, 10],
[7, 14],
[2, 5],
];
maxBoundary(N, V);
</script>
|
Time Complexity: O(N)
Auxiliary Space: O(N)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...