Maximize sum of MEX values of each node in an N-ary Tree
Last Updated :
03 May, 2023
Given an N-ary tree rooted at 1, the task is to assign values from the range [0, N – 1] to each node in any order such that the sum of MEX values of each node in the tree is maximized and print the maximum possible sum of MEX values of each node in the tree.
The MEX value of node V is defined as the smallest missing positive number in a tree rooted at node V.
Examples:
Input: N = 3, Edges[] = {{1, 2}, {1, 3}}
Output: 4
Explanation:
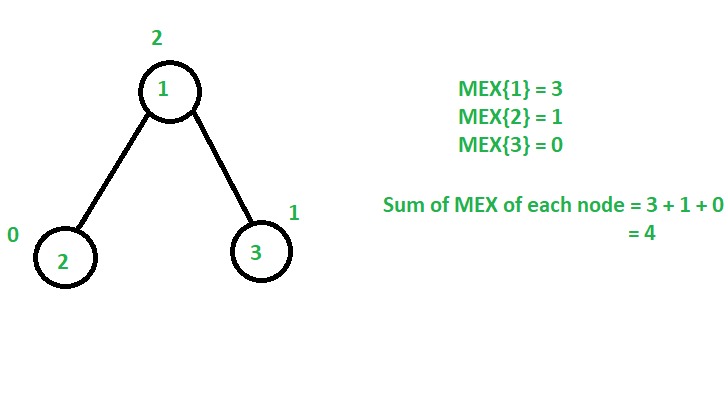
Assign value 0 to node 2, 1 to node 3 and 2 to node 1.
Therefore, the maximum sum of MEX of all nodes = MEX{1} + MEX{2} + MEX{3} = 3 + 1 + 0 = 4.
Input: N = 7, Edges[] = {1, 5}, {1, 4}, {5, 2}, {5, 3}, {4, 7}, {7, 6}}
Output: 13
Explanation:

Assign value 0 to node 6, 1 to node 7, 2 to node 4, 6 to node 1, 5 to node 5, 3 to node 2 and 4 to node 3.
Therefore, the maximum sum of MEX of all nodes = MEX{1} + MEX{2} + MEX{3} + MEX{4} + MEX{5} + MEX{6} + MEX{7} = 7 + 0 + 0 + 3 + 0 + 1 + 0 = 13.
Approach: The idea is to perform DFS Traversal on the given N-ary tree and find the sum of MEX for each subtree in the tree. Follow the steps below to solve the problem:
- Perform Depth First Search(DFS) on tree rooted at node 1.
- Initialize a variable mex with 0 and size with 1.
- Iterate through all children of the current node and perform the following operations:
- Recursively call the children of the current node and store the maximum sum of MEX among all subtree in mex.
- Increase the size of the tree rooted at the current node.
- Increase the value of mex by size.
- After completing the above steps, print the value of mex as the answer.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void makeTree(vector<int> tree[],
pair<int, int> edges[],
int N)
{
for (int i = 0; i < N - 1; i++) {
int u = edges[i].first;
int v = edges[i].second;
tree[u].push_back(v);
}
}
pair<int, int> dfs(int node,
vector<int> tree[])
{
int mex = 0;
int size = 1;
for (int u : tree[node]) {
pair<int, int> temp = dfs(u, tree);
mex = max(mex, temp.first);
size += temp.second;
}
return { mex + size, size };
}
int main()
{
int N = 7;
pair<int, int> edges[]
= { { 1, 4 }, { 1, 5 }, { 5, 2 }, { 5, 3 }, { 4, 7 }, { 7, 6 } };
vector<int> tree[N + 1];
makeTree(tree, edges, N);
cout << dfs(1, tree).first;
return 0;
}
|
Java
import java.util.*;
class GFG{
static class pair
{
int first, second;
public pair(int first, int second)
{
this.first = first;
this.second = second;
}
}
static void makeTree(Vector<Integer> tree[],
pair edges[], int N)
{
for(int i = 0; i < N - 1; i++)
{
int u = edges[i].first;
int v = edges[i].second;
tree[u].add(v);
}
}
static pair dfs(int node, Vector<Integer> tree[])
{
int mex = 0;
int size = 1;
for(int u : tree[node])
{
pair temp = dfs(u, tree);
mex = Math.max(mex, temp.first);
size += temp.second;
}
return new pair(mex + size, size);
}
public static void main(String[] args)
{
int N = 7;
pair edges[] = { new pair(1, 4),
new pair(1, 5),
new pair(5, 2),
new pair(5, 3),
new pair(4, 7),
new pair(7, 6) };
@SuppressWarnings("unchecked")
Vector<Integer>[] tree = new Vector[N + 1];
for(int i = 0; i < tree.length; i++)
tree[i] = new Vector<Integer>();
makeTree(tree, edges, N);
System.out.print((dfs(1, tree).first));
}
}
|
Python3
def makeTree(tree, edges, N):
for i in range(N - 1):
u = edges[i][0]
v = edges[i][1]
tree[u].append(v)
return tree
def dfs(node, tree):
mex = 0
size = 1
for u in tree[node]:
temp = dfs(u, tree)
mex = max(mex, temp[0])
size += temp[1]
return [mex + size, size]
if __name__ == '__main__':
N = 7
edges = [ [ 1, 4 ], [ 1, 5 ],
[ 5, 2 ], [ 5, 3 ],
[ 4, 7 ], [ 7, 6 ] ]
tree = [[] for i in range(N + 1)]
tree = makeTree(tree, edges, N)
print(dfs(1, tree)[0])
|
C#
using System;
using System.Collections.Generic;
class GFG{
public class pair
{
public int first, second;
public pair(int first, int second)
{
this.first = first;
this.second = second;
}
}
static void makeTree(List<int> []tree,
pair []edges, int N)
{
for(int i = 0; i < N - 1; i++)
{
int u = edges[i].first;
int v = edges[i].second;
tree[u].Add(v);
}
}
static pair dfs(int node, List<int> []tree)
{
int mex = 0;
int size = 1;
foreach(int u in tree[node])
{
pair temp = dfs(u, tree);
mex = Math.Max(mex, temp.first);
size += temp.second;
}
return new pair(mex + size, size);
}
public static void Main(String[] args)
{
int N = 7;
pair []edges = { new pair(1, 4),
new pair(1, 5),
new pair(5, 2),
new pair(5, 3),
new pair(4, 7),
new pair(7, 6) };
List<int>[] tree = new List<int>[N + 1];
for(int i = 0; i < tree.Length; i++)
tree[i] = new List<int>();
makeTree(tree, edges, N);
Console.Write((dfs(1, tree).first));
}
}
|
Javascript
<script>
function makeTree(tree, edges, N)
{
for (var i = 0; i < N - 1; i++) {
var u = edges[i][0];
var v = edges[i][1];
tree[u].push(v);
}
}
function dfs(node, tree)
{
var mex = 0;
var size = 1;
tree[node].forEach(u => {
var temp = dfs(u, tree);
mex = Math.max(mex, temp[0]);
size += temp[1];
});
return [mex + size, size ];
}
var N = 7;
var edges = [ [ 1, 4 ], [ 1, 5 ], [ 5, 2 ],
[ 5, 3 ], [ 4, 7 ], [ 7, 6 ] ];
var tree = Array.from(Array(N+1), ()=> Array());
makeTree(tree, edges, N);
document.write( dfs(1, tree)[0]);
</script>
|
Time Complexity: O(N)
Auxiliary Space: O(N)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...