Maximise count of intersections possible from the given endpoints of a line
Last Updated :
08 Mar, 2023
Given two parallel lines of length N and an array containing total N endpoints in array EndPoints[]. Given that there is a straight line from each i, such that 1 <= i <= N, such that each line should end at any of the EndPoint[j]. The task is to get the count of maximum number of intersections from the lines.
Notice: There should be a total of n lines drawn and every endpoint given in the array should be covered.
Example:
Input: 7
EndPoints[]: {4, 1, 4, 6, 7, 7, 5}
Output: 6
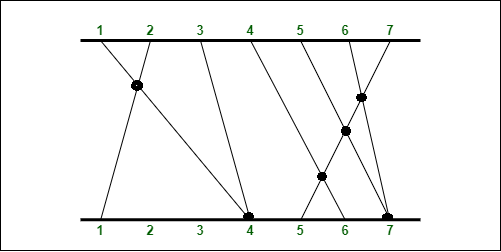
input 1
As you can see in the diagram above, a line is drawn from each i (1, 2, 3, 4, 5, 6, 7) and the endpoint is one of the values from EndPoints[] given in the input. It can be proven that there can not be more than 6 intersections in this case.
Input: 5
EndPoints[]: {2, 1, 4, 3, 5}
Output: 2
.png)
Input 2
Naive Approach:
Let’s look at two lines from i?EndPoints[i] and j?EndPoints[j].
- If ai<aj, there can never be any intersection.
- If ai>aj, there has to be an intersection.
- If ai=aj, it is possible that there is an intersection or not, depending on how we arrange the lines on the bottom terminal.
- In the last case, if there are multiple lines that go to the same segment ai, we can make all pairs of them cross by arranging the points in which they hit this segment from right to left.
Since we want to maximize the number of intersections, we just need to count the number of pairs (i,j) such that ai?aj. You can brute force all pairs in O(n2).
Below is the Implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void maximumIntersection(int EndPoints[], int n)
{
int total = 0;
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
if (EndPoints[i] >= EndPoints[j]) {
total++;
}
}
}
int first = EndPoints[0];
bool flag = false;
for (int i = 1; i < n; i++) {
if (EndPoints[i] != first) {
flag = false;
}
else {
flag = true;
}
}
if (flag == true) {
cout << "Maximum Intersection Possible: "
<< total / 2 << '\n';
}
else {
cout << "Maximum Intersection Possible: " << total
<< '\n';
}
}
int main()
{
int X = 7;
int EndPoints[] = { 4, 1, 4, 6, 7, 7, 5 };
int Y = 5;
int EndPoints2[] = { 2, 1, 4, 3, 5 };
int Z = 5;
int EndPoints3[] = { 1, 1, 1, 1, 1 };
maximumIntersection(EndPoints, X);
maximumIntersection(EndPoints2, Y);
maximumIntersection(EndPoints3, Z);
}
|
Java
import java.io.*;
import java.util.*;
class GFG {
static void maximumIntersection(int EndPoints[], int n)
{
int total = 0;
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
if (EndPoints[i] >= EndPoints[j]) {
total++;
}
}
}
int first = EndPoints[0];
boolean flag = false;
for (int i = 1; i < n; i++) {
if (EndPoints[i] != first) {
flag = false;
}
else {
flag = true;
}
}
if (flag == true) {
System.out.println( "Maximum Intersection Possible: "+ total / 2 );
}
else {
System.out.println( "Maximum Intersection Possible: " + total);
}
}
public static void main(String[] args)
{
int X = 7;
int EndPoints[] = { 4, 1, 4, 6, 7, 7, 5 };
int Y = 5;
int EndPoints2[] = { 2, 1, 4, 3, 5 };
int Z = 5;
int EndPoints3[] = { 1, 1, 1, 1, 1 };
maximumIntersection(EndPoints, X);
maximumIntersection(EndPoints2, Y);
maximumIntersection(EndPoints3, Z);
}
}
|
Python3
def maximum_intersection(endpoints, n):
total = 0
for i in range(n):
for j in range(i+1, n):
if endpoints[i] >= endpoints[j]:
total += 1
first = endpoints[0]
flag = False
for i in range(1, n):
if endpoints[i] != first:
flag = False
else:
flag = True
if flag:
print("Maximum Intersection possible: ", total//2)
else:
print("Maximum Intersection possible: ", total)
x = 7
endpoints = [4, 1, 4, 6, 7, 7, 5]
y = 5
endpoints2 = [2, 1, 4, 3, 5]
z = 5
endpoints3 = [1, 1, 1, 1, 1]
maximum_intersection(endpoints, x)
maximum_intersection(endpoints2, y)
maximum_intersection(endpoints3, z)
|
C#
using System;
public class GFG {
static void maximumIntersection(int[] EndPoints, int n)
{
int total = 0;
for (int i = 0; i < n; i++)
{
for (int j = i + 1; j < n; j++)
{
if (EndPoints[i] >= EndPoints[j]) {
total++;
}
}
}
int first = EndPoints[0];
bool flag = false;
for (int i = 1; i < n; i++)
{
if (EndPoints[i] != first) {
flag = false;
}
else {
flag = true;
}
}
if (flag == true) {
Console.WriteLine(
"Maximum Intersection Possible: "
+ total / 2);
}
else {
Console.WriteLine(
"Maximum Intersection Possible: " + total);
}
}
static public void Main()
{
int X = 7;
int[] EndPoints = { 4, 1, 4, 6, 7, 7, 5 };
int Y = 5;
int[] EndPoints2 = { 2, 1, 4, 3, 5 };
int Z = 5;
int[] EndPoints3 = { 1, 1, 1, 1, 1 };
maximumIntersection(EndPoints, X);
maximumIntersection(EndPoints2, Y);
maximumIntersection(EndPoints3, Z);
}
}
|
Javascript
function maximumIntersection( EndPoints, n)
{
let total = 0;
for (let i = 0; i < n; i++) {
for (let j = i + 1; j < n; j++) {
if (EndPoints[i] >= EndPoints[j]) {
total++;
}
}
}
let first = EndPoints[0];
let flag = false;
for (let i = 1; i < n; i++) {
if (EndPoints[i] != first) {
flag = false;
}
else {
flag = true;
}
}
if (flag == true) {
console.log( "Maximum Intersection Possible: "+ total / 2 );
}
else {
console.log( "Maximum Intersection Possible: " + total);
}
}
let X = 7;
let EndPoints = [ 4, 1, 4, 6, 7, 7, 5 ];
let Y = 5;
let EndPoints2 = [ 2, 1, 4, 3, 5 ];
let Z = 5;
let EndPoints3 = [ 1, 1, 1, 1, 1 ];
maximumIntersection(EndPoints, X);
maximumIntersection(EndPoints2, Y);
maximumIntersection(EndPoints3, Z);
|
Output
Maximum Intersection Possible: 6
Maximum Intersection Possible: 2
Maximum Intersection Possible: 5
Time Complexity: O(N2)
Auxiliary Space: O(1)
Efficient Approach:
The Basic idea is to use onset template policy based data structure and count frequency of duplicate elements and perform respective operations.
- The above approach can also be optimized if are able to count the number of pairs (i,j) such that ai?aj in an efficient manner.
- The ordered set keeps the unique elements in sorted order and provides a number of items strictly smaller than k, which is required in this problem.
order_of_key(k) : Number of items strictly smaller than k .
- Thus, we can loop over the input array and add each element one by one and can check order_of_key(element) at each iteration to get the number of elements less than the element and add that to our sum.
- we will have to count the running frequency of each element because we know that equal elements also intersect each other, thus we will be adding the running frequencies to our answer as well.
Below is the Implementation of the above approach:
C++
#include <iostream>
using namespace std;
#include <ext/pb_ds/assoc_container.hpp> // Common file
#include <ext/pb_ds/tree_policy.hpp>
#include <functional> // for less
#include <iostream>
using namespace std;
using namespace __gnu_pbds;
template <class T>
using oset
= tree<T, null_type, greater_equal<T>, rb_tree_tag,
tree_order_statistics_node_update>;
void maximumIntersection(int EndPoints[], int N)
{
oset<int> st;
int ans = 0;
map<int, int> mp;
for (int i = 0; i < N; i++) {
st.insert(EndPoints[i]);
ans += st.order_of_key(EndPoints[i])
+ mp[EndPoints[i]];
mp[EndPoints[i]]++;
}
if (mp.size() == 1) {
cout << "Maximum Intersection Possible: " << ans / 2
<< "\n";
}
else {
cout << "Maximum Intersection Possible: " << ans
<< "\n";
}
}
int main()
{
int X = 7;
int EndPoints[] = { 4, 1, 4, 6, 7, 7, 5 };
int Y = 5;
int EndPoints2[] = { 2, 1, 4, 3, 5 };
int Z = 5;
int EndPoints3[] = { 1, 1, 1, 1, 1 };
maximumIntersection(EndPoints, X);
maximumIntersection(EndPoints2, Y);
maximumIntersection(EndPoints3, Z);
}
|
Output
Maximum Intersection Possible: 6
Maximum Intersection Possible: 2
Maximum Intersection Possible: 5
Time Complexity: O(N*logN)
Auxiliary Space: O(N)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...