Maximal Frequent Itemsets
Last Updated :
27 Mar, 2023
Prerequisite: Apriori Algorithm & Frequent Item Set Mining
The number of frequent itemsets generated by the Apriori algorithm can often be very large, so it is beneficial to identify a small representative set from which every frequent itemset can be derived. One such approach is using maximal frequent itemsets.
A maximal frequent itemset is a frequent itemset for which none of its immediate supersets are frequent. To illustrate this concept, consider the example given below:
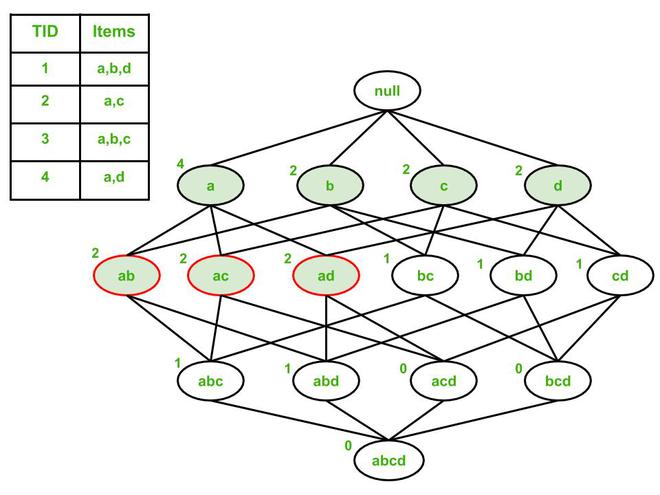
The support counts are shown on the top left of each node. Assume support count threshold = 50%, that is, each item must occur in 2 or more transactions. Based on that threshold, the frequent itemsets are a, b, c, d, ab, ac, and ad (shaded nodes).
Out of these 7 frequent itemsets, 3 are identified as maximal frequent (having red outline):
- ab: Immediate supersets abc and abd are infrequent.
- ac: Immediate supersets abc and acd are infrequent.
- ad: Immediate supersets abd and bcd are infrequent.
The remaining 4 frequent nodes (a, b, c, and d) cannot be maximal frequent because they all have at least 1 immediate superset that is frequent.
Advantage: Maximal frequent itemsets provide a compact representation of all the frequent itemsets for a particular dataset. In the above example, all frequent itemsets are subsets of the maximal frequent itemsets, since we can obtain sets a, b, c, and d by enumerating subsets of ab, ac, and ad (including the maximal frequent itemsets themselves).
Disadvantage: The support count of maximal frequent itemsets does not provide any information about the support count of their subsets. This means that an additional traversal of data is needed to determine the support count for non-maximal frequent itemsets, which may be undesirable in certain cases.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...