Matrix Diagonalization
Last Updated :
27 Apr, 2022
Prerequisite: Eigenvalues and eigenvectors
Let A and B be two matrices of order n. B can be considered similar to A if there exists an invertible matrix P such that B=P^{-1} A P This is known as Matrix Similarity Transformation.
Diagonalization of a matrix is defined as the process of reducing any matrix A into its diagonal form D. As per the similarity transformation, if the matrix A is related to D, then
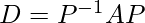 and the matrix A is reduced to the diagonal matrix D through another matrix P. Where P is a modal matrix)
and the matrix A is reduced to the diagonal matrix D through another matrix P. Where P is a modal matrix)
Modal matrix: It is a (n x n) matrix that consists of eigen-vectors. It is generally used in the process of diagonalization and similarity transformation.
In simpler words, it is the process of taking a square matrix and converting it into a special type of matrix called a diagonal matrix.
Steps Involved:
Step 1: Initialize the diagonal matrix D as:
![Rendered by QuickLaTeX.com D=\left[\begin{array}{ccc} \lambda_{1} & 0 & 0 \\ 0 & \lambda_{2} & 0 \\ 0 & 0 & \lambda_{3} \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3cee524be22e1360cec9e36c6dc6e6ac_l3.png)
where λ1, λ2, λ3 -> eigen values
Step 2: Find the eigen values using the equation given below.
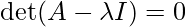
where, A -> given 3×3 square matrix. I -> identity matrix of size 3×3. λ -> eigen value.
Step 3: Compute the corresponding eigen vectors using the equation given below.
![Rendered by QuickLaTeX.com \begin{array}{l} A t, \lambda=i \\ {[A-\lambda I] X_{i}=0} \end{array}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2412ee29fc689f726190dc0b6eb3567e_l3.png)
where, λi -> eigen value. Xi -> corresponding eigen vector.
Step 4: Create the modal matrix P.
![Rendered by QuickLaTeX.com P=\left[X_{0} X_{1} . . X_{n}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1501c321c6a7de3dde2e22e6e27062da_l3.png)
Here, all the eigenvectors till Xi have filled column-wise in matrix P.
Step 5: Find P-1 and then use the equation given below to find diagonal matrix D.
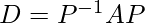
Example Problem:
Problem Statement: Assume a 3×3 square matrix A having the following values:
![Rendered by QuickLaTeX.com A=\left[\begin{array}{ccc} 1 & 0 & -1 \\ 1 & 2 & 1 \\ 2 & 2 & 3 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7f7076d949d44df81d04a07e77719019_l3.png)
Find the diagonal matrix D of A using the diagonalization of the matrix. [ D = P-1AP ]
Solution:
Step 1: Initializing D as:
![Rendered by QuickLaTeX.com D=\left[\begin{array}{ccc} \lambda_{1} & 0 & 0 \\ 0 & \lambda_{2} & 0 \\ 0 & 0 & \lambda_{3} \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3cee524be22e1360cec9e36c6dc6e6ac_l3.png)
Step 2: Find the eigen values. (or possible values of λ)
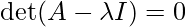
![Rendered by QuickLaTeX.com \begin{array}{l} \Longrightarrow \operatorname{det}(A-\lambda I)=\operatorname{det}\left(\left[\begin{array}{ccc} 1-\lambda & 0 & -1 \\ 1 & 2-\lambda & 1 \\ 2 & 2 & 3-\lambda \end{array}\right]\right)=0 \\ \Longrightarrow\left(\lambda^{3}-6 \lambda^{2}+11 \lambda-6\right)=0 & \\ \Longrightarrow(\lambda-1)(\lambda-2)(\lambda-3)=0 \\ \Longrightarrow & \lambda=1,2,3 \end{array}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-aecb25e925f13c740b8dafd0698fd52d_l3.png)
Step 3: Find the eigen vectors X1, X2, X3 corresponding to the eigen values λ = 1,2,3.
![Rendered by QuickLaTeX.com At $\lambda=1$ A - $(1) I$ $X_{1}=0$ $\Longrightarrow\left[\begin{array}{ccc}1-1 & 0 & -1 \\ 1 & 2-1 & 1 \\ 2 & 2 & 3-1\end{array}\right]\left[\begin{array}{l}x_{1} \\ x_{2} \\ x_{3}\end{array}\right]=\left[\begin{array}{l}0 \\ 0 \\ 0\end{array}\right]$ $\Longrightarrow\left[\begin{array}{ccc}0 & 0 & -1 \\ 1 & 1 & 1 \\ 2 & 2 & 2\end{array}\right]\left[\begin{array}{l}x_{1} \\ x_{2} \\ x_{3}\end{array}\right]=\left[\begin{array}{l}0 \\ 0 \\ 0\end{array}\right]$ On solving, we get the following equations: $x_{3}=0\left(x_{1}\right)$ $x_{1}+x_{2}=0 \Longrightarrow x_{2}=-x_{1}$ $\therefore X_{1}=\left[\begin{array}{c}x_{1} \\ -x_{1} \\ 0\left(x_{1}\right)\end{array}\right]$ $\Longrightarrow X_{1}=\left[\begin{array}{c}1 \\ -1 \\ 0\end{array}\right]$ Similarly, for $\lambda=2$ $X_{2}=\left[\begin{array}{c}-2 \\ 1 \\ 2\end{array}\right]$ and for $\lambda=3$ $X_{3}=\left[\begin{array}{c}1 \\ -1 \\ -2\end{array}\right]$](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-54df2258de67c7cf854e845a2919dc0c_l3.png)
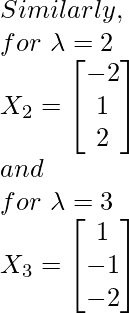
Step 5: Creation of modal matrix P. (here, X1, X2, X3 are column vectors)
![Rendered by QuickLaTeX.com P=\left[X_{1} X_{2} X_{3}\right]=\left[\begin{array}{ccc} 1 & -2 & 1 \\ -1 & 1 & -1 \\ 0 & 2 & -2 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-09e5d83615881301779f489beb4f4c6b_l3.png)
Step 6: Finding P-1 and then putting values in diagonalization of a matrix equation. [D = P-1AP]
We do Step 6 to find out which eigenvalue will replace λ1, λ2, and λ3 in the initial diagonal matrix created in Step 1.
![Rendered by QuickLaTeX.com \begin{array}{l} \begin{array}{l} \quad P=\left[\begin{array}{ccc} 1 & -2 & 1 \\ -1 & 1 & -1 \\ 0 & 2 & -2 \end{array}\right] \\ \operatorname{det}(P)=(1)[(-2)(1)-(-1)(2)]-(-2)[(-2)(-1)-(0)(-1)]+(1)[(2)(-1)- \\ (0)(1)] \\ =[0+(4)+(-2)] \\ =2 \end{array}\\ \text { Since } \operatorname{det}(P) \neq 0 \Longrightarrow \text { Matrix } P \text { is invertible. } \end{array}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-95a4873225048341204822e8e209f569_l3.png)
We know that 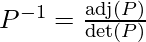
On solving, we get ![Rendered by QuickLaTeX.com P^{-1}=\frac{1}{2}\left[\begin{array}{ccc} 0 & -2 & 1 \\ -2 & -2 & 0 \\ -2 & -2 & -1 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9a106923a45ac3b418199d0adac54ab7_l3.png)
Putting in the Diagonalization of Matrix equation, we get
![Rendered by QuickLaTeX.com \begin{array}{l} \quad D=P^{-1} A P \\ D=\frac{1}{2}\left[\begin{array}{ccc} 0 & -2 & 1 \\ -2 & -2 & 0 \\ -2 & -2 & -1 \end{array}\right]\left[\begin{array}{ccc} 1 & 0 & -1 \\ 1 & 2 & 1 \\ 2 & 2 & 3 \end{array}\right]\left[\begin{array}{ccc} 1 & -2 & 1 \\ -1 & 1 & -1 \\ 0 & 2 & -2 \end{array}\right] \\ D=\left[\begin{array}{lll} 1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 3 \end{array}\right] \end{array}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-701b5697ed528cee5a6dafd21522243b_l3.png)
Matlab
clear all
clc
disp("MATLAB Implementation for Diagonalization
of a Square Matrix | GeeksforGeeks")
A = input("Enter a matrix A : ");
[P , D] = eig(A);
D1 = inv(P)*(A)*(P);
disp("Diagonal form 'D' of Input Matrix 'A' is:")
disp(D1)
|
Output:
For the Matrix: 
For the Matrix: 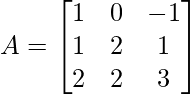
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...