MATLAB – Trapezoidal numerical integration without using trapz

Last Updated : 04 Jul, 2021

Trapezoidal rule is utilized to discover the approximation of a definite integral. The main idea in the Trapezoidal rule is to accept the region under the graph of the given function to be a trapezoid rather than a rectangle shape and calculate its region.

The formula for numerical integration using trapezoidal rule is:

$∫_a^bf(x)dx=h/2[ f(a)+2\{ ∑^{n-1}_{i=1}f(a+ih)\} +f(b)]$

where h = (b-a)/n

Now we take an example for calculating the area under the curve 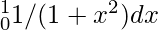$∫_0^11/(1+x^2) dx$ using 10 subintervals.

Example:

Matlab

% MATLAB program for calculate the  
% area under the curve ∫_0^11/(1+x^2) dx  
% using 10 subintervals specify the variable 
% x as symbolic ones The syms function creates  
% a variable dynamically and automatically assigns 
% to a MATLAB variable with the same name 
syms x 
  
% Lower Limit 
a=0;   
  
% Upper Limit 
b=1;    
  
% Number of segments 
n=10;  
  
% Declare the function 
f1=1/(1+x^2); 
  
% inline creates a function of 
% string containing in f1 
f=inline(f1);  
  
% h is the segment size 
h=(b - a)/n; 
  
% X stores the summation of first 
% and last segment 
X=f(a)+f(b); 
  
% variable R stores the summation of 
% all the terms from 1 to n-1 
R=0; 
for i = 1:1:n-1 
    xi=a+(i*h); 
    R=R+f(xi); 
end
  
% Formula to calculate numerical integration 
% using Trapezoidal Rule 
I=(h/2)*(X+2*R); 
  
% Display the output 
disp('Area under the curve 1/(1+x^2) = '); 
disp(I);

Output:

Let’s take another example for calculating the area under the curve 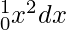$∫_0^1x^2 dx$ using 4 subintervals.

Example:

Matlab

% MATLAB program for calculate 
% the area under the curve∫_0^1x^2 dx     
% using 4 subintervals. 
% specify the variable x as symbolic ones 
  
syms x 
  
% Lower Limit 
a=0;  
  
% Upper Limit 
b=1;  
  
% Number of segments 
n=4;   
  
% Declare the function 
f1=x^2; 
  
% inline creates a function of 
% string containing in f1 
f=inline(f1);  
  
% h is the segment size 
h=(b - a)/n; 
X=f(a)+f(b); 
  
% variable R stores the summation  
% of all the terms from 1 to n-1 
R=0; 
for i = 1:1:n-1 
    xi=a+(i*h); 
    R=R+f(xi); 
end
  
% Formula to calculate numerical 
% integration using Trapezoidal Rule 
I=(h/2)*(X+2*R); 
  
% Display the output 
disp('Area under the curve x^2 = '); 
disp(I); 