Maths Commands in LaTeX
Last Updated :
20 Jun, 2020
LATEX is a document preparation system for producing professional-looking documents. LaTeX is widely used for the communication and publication of scientific documents in many fields, including mathematics, statistics, computer science, engineering, physics, etc. It also has a prominent role in the preparation and publication of books and articles that contain complex multilingual materials, such as Sanskrit and Greek.
So in this post we have discussed the most used TEX commands used for Maths.
- Fractions:
Instead of writing fractions as A / B we will use below syntax
Syntax :
\frac{numerator}{denominator}
Example –
\frac{a+1}{b+1}
OUTPUT:
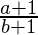
- Nth power:
Instead of writing powers as x ^ n which is not clear as if it is xor or power so we will use below syntax
Syntax:
x^y
Example –
x^2
OUTPUT:
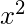
- Nth root:
Instead of writing roots as x^(1/N) which is not clear as if it is xor or root so we will use below syntax
Syntax:
\sqrt[N]{27}
Example –
\sqrt[3]{27}
OUTPUT:
![Rendered by QuickLaTeX.com \sqrt[3]{27}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-dc99d3599ed0ae91dd93e49687b93aee_l3.png)
- Matrices
Instead of writing matrices as [[1, x, x^2], [1, y, y^2][1, z, z^2]] which is not very clear use below syntax
Syntax:
\begin{matrix}
1 & x & x^2 \\
1 & y & y^2 \\
1 & z & z^2 \\
\end{matrix}
Example –
\begin{matrix}
1 & x & x^2 \\
1 & y & y^2 \\
1 & z & z^2 \\
\end{matrix}
OUTPUT:
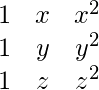
- Definitions by cases (piecewise function) is a function defined by multiple sub-functions, each sub-function applying to a certain interval of the main function’s domain, a sub-domain.
Syntax:
f(n) =
\begin{cases}
n/2, & \text{if $n$ is even} \\
n+1, & \text{if $n$ is odd}
\end{cases}
Example –
f(n) =
\begin{cases}
n/2, & \text{if $n$ is even} \\
n+1, & \text{if $n$ is odd}
\end{cases}
OUTPUT:
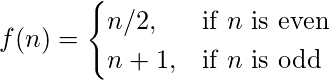
- System of equations is a function defined by multiple sub-functions, each sub-function applying to a certain interval of the main function’s domain, a sub-domain.
Syntax:
\left\{
\begin{array}{c}
a_1x+b_1y+c_1z=d_1 \\
a_2x+b_2y+c_2z=d_2 \\
a_3x+b_3y+c_3z=d_3
\end{array}
\right.
Example –
\left\{
\begin{array}{c}
a_1x+b_1y+c_1z=d_1 \\
a_2x+b_2y+c_2z=d_2 \\
a_3x+b_3y+c_3z=d_3
\end{array}
\right.
OUTPUT:

- Summation is the addition of a sequence of any kind of numbers, called addends or summands; the result is their sum or total.
Syntax:
\sum_{i=0}^n i^2
Example –
\sum_{i=0}^n i^2
OUTPUT:
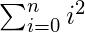
- subscriptsis a character that is set slightly below the normal line of type.
Syntax:
\log_2 x
Example –
\log_2 x
OUTPUT:
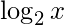
- floor is the function that takes as input a real number and gives as output the greatest integer less than or equal to, denoted.
Syntax:
\lfloor n \rfloor
Example –
\lfloor 2.2 \rfloor
OUTPUT:
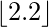
- ceil function maps to the least integer greater than or equal to, denoted.
Syntax:
\lceil n \rcei
Example –
\lceil 2.5 \rceil
OUTPUT:
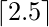
- Some Combined examples :
Example –
- Use
\sum_{i=0}^n i^2 = \frac{(n^2+n)(2n+1)}{6} for 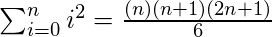
Example –
- Use
\left(\frac{\sqrt x}{y^3}\right) for 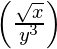
Example –
- Use
\Biggl(\biggl(\Bigl(\bigl((n)\bigr)\Bigr)\biggr)\Biggr)
for 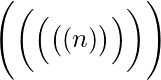
Example –
- Use
\sqrt[3]{\frac xy} for ![Rendered by QuickLaTeX.com \sqrt[3]{\frac xy}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3052e669790f13a6d917962af892ce11_l3.png)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...