Combinatorics is the branch of Mathematics dealing with the study of finite or countable discrete structures. It includes the enumeration or counting of objects having certain properties. Counting helps us solve several types of problems such as counting the number of available IPv4 or IPv6 addresses.
Counting Principles: There are two basic counting principles, sum rule, and the product rule.
Sum Rule – If a task can be done in one of 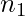 ways or one of
ways or one of 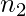 ways, where none of the set of
ways, where none of the set of 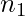 ways is the same as any of the set of
ways is the same as any of the set of 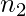 ways, then there are
ways, then there are 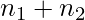 ways to do the task.
ways to do the task.
Product Rule – If a task can be broken down into a sequence of 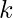 subtasks, where each subtask can be performed in
subtasks, where each subtask can be performed in 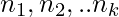 respectively, then the total number of ways the task can be performed is
respectively, then the total number of ways the task can be performed is 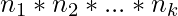 .
.
- Example 1 – In how many ways can 3 winning prizes be given to the top 3 players in a game played by 12 players?
- Solution – We have to distribute 3 prizes among 12 players. This task can be divided into 3 subtasks of assigning a single prize to a certain player.
Giving out the first prize can be done in 12 different ways. After giving out the first prize, two prizes remain and 11 players remain. Similarly, the second prize and third prize can be given in 11 ways and 10 ways. The total number of ways by the product rule is 12 * 11 * 10 = 1320.
- Example 2 – In how many ways can a person choose a project from three lists of projects of sizes 10, 15, and 19 respectively?
- Solution – The person has a choice of choosing a project from either of the three lists. So the person can choose from either 10 projects or 15 projects or 19 projects. Since choosing from one list is not the same as choosing another list, the total number of ways of choosing a project by the sum-rule is 10 + 15 + 19 = 44.
- Example 3 – How many distinct license plates are possible in the given format- Two alphabets in uppercase, followed by two digits then a hyphen, and finally four digits. Sample- AB12-3456.
- Solution – There are 26 possibilities for each of the two letters and 10 possibilities for each of the digits. Therefore the total number of possibilities is – 26 * 26 * 10 * 10 * 10 * 10 * 10 * 10 = 676000000.
- Example 4 – How many variable names of length upto 3 exist if the variable names are alphanumeric and case-sensitive with the restriction that the first character has to be an alphabet?
- Solution – Let
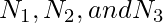 denote the number of possible variable names of lengths 1, 2, and 3. Therefore, the total number of variable names is
denote the number of possible variable names of lengths 1, 2, and 3. Therefore, the total number of variable names is 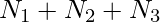 .
.
For 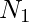 there are only 52 possibilities since the first character has to be an alphabet.
there are only 52 possibilities since the first character has to be an alphabet.
For 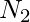 , there are 52 * 62 = 3224 possibilities
, there are 52 * 62 = 3224 possibilities
For 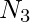 , there are 52 * 62 * 62 = 199888 possibilities
, there are 52 * 62 * 62 = 199888 possibilities
Therefore, total number of variable names = 52 + 3224 + 199888 = 203164
Principle of Inclusion-Exclusion :
The sum rule mentioned above states that if there are multiple sets of ways of doing a task, there shouldn’t be any way that is common between two sets of ways because if there is, it would be counted twice and the enumeration would be wrong.
The principle of inclusion-exclusion says that in order to count only unique ways of doing a task, we must add the number of ways to do it in one way and the number of ways to do it in another and then subtract the number of ways to do the task that are common to both sets of ways.
The principle of inclusion-exclusion is also known as the subtraction principle. For two sets of ways 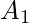 and
and 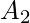 , the enumeration would like this-
, the enumeration would like this-
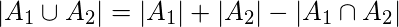

|A ? B| = |A| +|B| ?|A ? B|
Example 1 – How many binary strings of length 8 either start with a ‘1’ bit or end with two bits ’00’?
Solution – If the string starts with one, there are 7 characters left which can be filled in 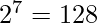 ways.
ways.
If the string ends with ’00’ then 6 characters can be filled in 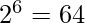 ways.
ways.
Now if we add the above sets of ways and conclude that it is the final answer, then it would be wrong. This is because there are strings with start with ‘1’ and end with ’00’ both, and since they satisfy both criteria they are counted twice.
So we need to subtract such strings to get a correct count.
Strings that start with ‘1’ and end with ’00’ have five characters that can be filled in 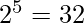 ways.
ways.
So by the inclusion-exclusion principle we get-
Total strings = 128 + 64 – 32 = 160
Example 2 – How many numbers between 1 and 1000, including both, are divisible by 3 or 4?
Solution – Number of numbers divisible by 3 = 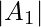 =
=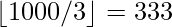 .
.
Number of numbers divisible by 4 = 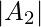 =
= 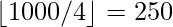 .
.
Number of numbers divisible by 3 and 4 = 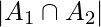 =
= 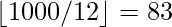 .
.
Therefore, number of numbers divisible by 3 or 4 = 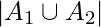 = 333 + 250 – 83 = 500
= 333 + 250 – 83 = 500
In the same way, we can be applied when the number of sets is larger. suppose there
are three sets, the inclusion-exclusion formula will be
|A ? B ? C| = |A| +|B| +|C| ?|A ? B| ?|A ? C| ?|B ? C| +|A ? B ? C|
the corresponding diagram will look like this:

the inclusion-exclusion formula for 3 sets
And if you try to generalize for n-sets, the size of the union X1 ? X2 ? ··· ? Xn can be calculated by going through all possible intersections that contain some of the sets X1, X2,…, Xn. If the intersection contains an odd number of sets, its size is added to the answer, and otherwise, its size is subtracted from the answer.
Similar formulas for calculating the size of an intersection:
|A ?B | = |A| +|B| ?|A ? B|
and,
|A ? B ? C| = |A| +|B| +|C| ?|A ? B| ?|A ? C| ?|B ? C| +|A ? B ? C|
Derangements
In order to understand derangements let’s, take an example, count the number of derangements of elements {1,2,…,n}, i.e., permutations where no element remains in its original place. when n = 3, there are two derangements: (2,3,1) and (3,1,2).
One way for solving the problem is to use inclusion-exclusion, Let Xk be the set of permutations that contain the element k at position k. for n = 3, the sets are as follows:
X1 = {(1,2,3),(1,3,2)}
X2 = {(1,2,3),(3,2,1)}
X3 = {(1,2,3),(2,1,3)}
Using these sets, the number of derangements equals
n!?|X1 ? X2 ?··· ? Xn |,
Using inclusion-exclusion reduces to calculating sizes of intersections which can be done easily, for n=3, the size of |X1 ? X2 ? X3| is
=> |X1| +|X2| +|X3| ?|X1 ? X2| ?|X1 ? X3| ?|X2 ? X3| +|X1 ? X2 ? X3|
=> 2+2+2?1?1?1+1
=> 4
So the number of solutions will be 3!?4 = 2. Well, this problem can also be solved without using inclusion-exclusion. Let’s say f(n) denotes the number of derangements for {1,2,…,n}. So, I can write the recursive formula in this manner,

recursive formula
The formula can be derived by considering the possibilities of how element 1 changes in the derangement. There are n?1 ways to choose an element x that replaces element 1. In each such choice, there are two ways: first way : We also replace the element x with the element 1. After this, the remaining task is to construct a derangement of n?2 elements. second way: We replace the element x with some other element than 1. Now we have to construct a derangement of the n?1 element, because we cannot replace the element x with the element 1, and all other elements must be changed.
GATE CS Corner Questions
Practicing the following questions will help you test your knowledge. All questions have been asked in GATE in previous years or in GATE Mock Tests. It is highly recommended that you practice them.
1. GATE CS 2007, Question 3
2. GATE CS 2004, Question 26
Find the next Article @ Pigeonhole Principle
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...