Program for Markov matrix
Last Updated :
20 Feb, 2023
Given a m x n 2D matrix, check if it is a Markov Matrix.
Markov Matrix : The matrix in which the sum of each row is equal to 1.
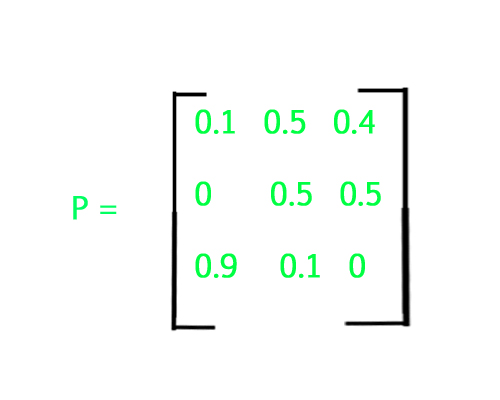
Example of Markov Matrix
Examples:
Input :
1 0 0
0.5 0 0.5
0 0 1
Output : yes
Explanation :
Sum of each row results to 1,
therefore it is a Markov Matrix.
Input :
1 0 0
0 0 2
1 0 0
Output : no
Approach : Initialize a 2D array, then take another single dimensional array to store the sum of each rows of the matrix, and check whether all the sum stored in this 1D array is equal to 1, if yes then it is Markov matrix else not.
Implementation:
C++
#include <iostream>
using namespace std;
#define n 3
bool checkMarkov(double m[][n])
{
for (int i = 0; i <n; i++) {
double sum = 0;
for (int j = 0; j < n; j++)
sum = sum + m[i][j];
if (sum != 1)
return false;
}
return true;
}
int main()
{
double m[3][3] = { { 0, 0, 1 },
{ 0.5, 0, 0.5 },
{ 1, 0, 0 } };
if (checkMarkov(m))
cout << " yes ";
else
cout << " no ";
}
|
Java
import java.io.*;
public class markov
{
static boolean checkMarkov(double m[][])
{
for (int i = 0; i < m.length; i++) {
double sum = 0;
for (int j = 0; j < m[i].length; j++)
sum = sum + m[i][j];
if (sum != 1)
return false;
}
return true;
}
public static void main(String args[])
{
double m[][] = { { 0, 0, 1 },
{ 0.5, 0, 0.5 },
{ 1, 0, 0 } };
if (checkMarkov(m))
System.out.println(" yes ");
else
System.out.println(" no ");
}
}
|
Python3
def checkMarkov(m) :
for i in range(0, len(m)) :
sm = 0
for j in range(0, len(m[i])) :
sm = sm + m[i][j]
if (sm != 1) :
return False
return True
m = [ [ 0, 0, 1 ],
[ 0.5, 0, 0.5 ],
[ 1, 0, 0 ] ]
if (checkMarkov(m)) :
print(" yes ")
else :
print(" no ")
|
C#
using System;
class GFG
{
static bool checkMarkov(double [,]m)
{
for (int i = 0;
i < m.GetLength(0); i++)
{
double sum = 0;
for (int j = 0;
j < m.GetLength(1); j++)
sum = sum + m[i, j];
if (sum != 1)
return false;
}
return true;
}
static void Main()
{
double [,]m = new double[,]{{ 0, 0, 1},
{0.5, 0, 0.5},
{1, 0, 0}};
if (checkMarkov(m))
Console.WriteLine(" yes ");
else
Console.WriteLine(" no ");
}
}
|
PHP
<?php
function checkMarkov($m)
{
$n = 3;
for ($i = 0; $i <$n; $i++)
{
$sum = 0;
for ($j = 0; $j < $n; $j++)
$sum = $sum + $m[$i][$j];
if ($sum != 1)
return false;
}
return true;
}
$m = array(array(0, 0, 1),
array(0.5, 0, 0.5),
array(1, 0, 0));
if (checkMarkov($m))
echo " yes ";
else
echo " no ";
?>
|
Javascript
<script>
let n = 3
function checkMarkov( m)
{
for (let i = 0; i <n; i++) {
let sum = 0;
for (let j = 0; j < n; j++)
sum = sum + m[i][j];
if (sum != 1)
return false;
}
return true;
}
let m = [ [ 0, 0, 1 ],
[ 0.5, 0, 0.5 ],
[ 1, 0, 0 ] ];
if (checkMarkov(m))
document.write(" yes ");
else
document.write(" no ");
</script>
|
Time Complexity: O(n2)
Auxiliary Space: O(1), since no extra space has been taken.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...