Moving charges is an electric current that passes through a fixed point in a fixed period of time. Moving charges are responsible for establishing the magnetic field. The magnetic field is established due to the force exerted by the flow of moving charges. As the magnetic field is established moving charges start acting like a magnet.
Magnetic Effect of Current when current is flowing through the conductor, a magnetic field is established around it. This phenomenon is called the magnetic effect of electric current.
Behavior of Charged particle in the magnetic field
When the charged particle moves through the magnetic field it experiences a force on it. When the charged particle q moves with the velocity v in the magnetic field B and the velocity of the particle is perpendicular to the direction of the magnetic field then force acting on it is given by F = q(v × B). Hence, the magnetic force is directed towards the circular motion of the particle and acts as a centripetal force. Thus if v and B are perpendicular to each other, the particle moves in a circle. Thus, the particle moves in the helical motion when the two components are acting perpendicular. When the particle moves along the direction of the magnetic field then no effect is felt upon it.
Ampere’s Circuit Law
The line integral of the magnetic field in a closed path is equal to the μ0 times the net current passing through that closed path or loop.
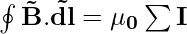
Biot – Savart Law
According to Biot-Savart law magnetic field at a point due to very small current element dl depends upon
- directly proportional to the current(I)
dB ∝ l…….eq(1)
- directly proportional to the length of an element(dl)
dB ∝ dl…….eq(2)
- directly proportional to sinθ
dB ∝ sinθ……..eq(3)
- inversely proportional to r2
dB ∝ (1 / r2)……..eq(4)
combining equations 1,2,3 and 4 we get
dB ∝ (I dl sinθ ) / r2
dB = (k I dl sinθ ) / r2
If, k =1
dB = ( I dl sinθ ) / r2
The magnetic field dB at a point P associated with a length element dl of a wire carrying a steady current I is given by
dB = 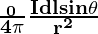
μ0 is the permeability of free space
μ0/4π = 10-7 Henry/meter
Biot – Savart law in vector form
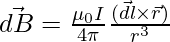
The direction of 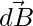 is perpendicular to the plane determined by
is perpendicular to the plane determined by 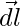 and
and 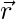 .
.
Application of Biot-Savart’s Law
- This law is used to calculate the magnetic reactions on the molecular or atomic level.
- It can be used in aerodynamics for determining the velocity of vortex lines.
Importance of Biot-Savart’s Law
- This law is applicable for even very small current carrying conductors.
- This law resembles Coulomb’s law in electrostatics.
- This law is used in the symmetric current distribution.
Magnetic Field on the Axis of a Circular Current Loop
Let us suppose a circular current loop of radius a and magnetic field at a distance of x unit along its axis is required then,
a is the radius of the circular current loop
I is the current flowing through the circular current loop
dB1 and dB2 are the magnetic fields
dl is the very small length of wire of the loop
x is the distance of P from center O of the loop
From the Biot Savart law,
The direction of the magnetic field is perpendicular to the plane determined by dl and r
Therefore, r2 = x2 + a2
Magnetic field due to current element dl remains same
dB1 = dB2 = 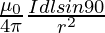
dB1 = dB2 = 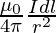
The vertical component cancel the effect of each other
The magnetic field at point P is given by
B = ∫ dB sinθ
B = ∫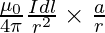 [ sinθ = a / r ]
[ sinθ = a / r ]
B = 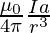 ×∫dl
×∫dl
B = 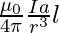 [ l = 2πa and r = (x2 + r2)1/2]
[ l = 2πa and r = (x2 + r2)1/2]
B = 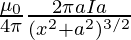
B = 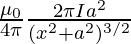
B = 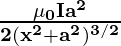
Case 1: If the observation point is at the center of the loop
At the center of loop x = 0
B = 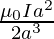
B = 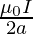
Case 2: If the observation point is far away from the loop
If the observation point is far away from the loop, then a << x so, a2 can be neglected in comparison to x2
B = 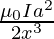
Note:
If there is a coil of N turns then the magnetic field is given by
B = 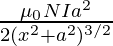
Right-Hand Thumb Rule
If we hold the thumb of the right hand mutually perpendicular to the grip of the fingers such that the curls of the fingers represent the direction of current in the wire loop, then the thumb of the right hand will point in the direction of the magnetic field near the center of the current loop.
Practise Problems based on Magnetic Field on the Axis of a Circular Current Loop
Problem 1: Magnetic field intensity at the center of a coil of 50 turns, radius 0.5 m, and carrying a current of 2A is ________.
Solution:
Magnetic field at the center of the coil is given by
B = 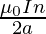
= (4 π ×10-7 × 2 × 50) / (2 × 0.5)
B = 1.25 × 10-4 T
Problems 2: An electric current is flowing in a circular loop of radius r. At what distance from the center on the axis of the loop will the magnetic field be 1/8th of its value at the center?
Solution:
Magnetic field at the center of the circular loop B1 is given by
B = 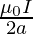
Magnetic field at any distance x of the circular loop B2 is given by
B = 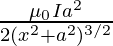
According to the question
B1 = (1/8) B2
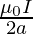 = (1/8)
= (1/8)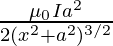
r3 / (r2 + x2)3/2 = 1/8
[ r / (r2 + x2)1/2 ]3 = 1/8
r / (r2 + x2)1/2 = 1/ 3√8
r / (r2 + x2)1/2 = 1/2
2r = (r2 + x2)1/2
Squaring both sides
4r2 = r2 + x2
x2 = 3r2
x = √3 r
Problem 3: Magnetic field intensity at the center of a circular current loop, radius 0.4 m, and carrying a current of 3A is ________.
Solution:
Magnetic field at the center of the coil is given by
B = 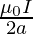
B = (4 π ×10-7 × 3) / (2 × 0.4)
B = 4.71×10-6 T
FAQs on Magnetic Field
Question 1: Where is the intensity of the magnetic field strongest in a circular loop?
Answer:
The intensity of magnetic field is strongest at the center of the circular loop.
Question 2: State the equation for the magnetic field on the axis of the current carrying coil of N turns.
Answer:
The equation for the magnetic field on the axis of the current carrying coil is given by
B = 
Question 3: State the equation for the magnetic field on the axis of the current carrying loop.
Answer:
The equation for the magnetic field on the axis of the current carrying loop is given by
B = 
Question 4: State Biot Savart law and its formula.
Answer:
The magnetic field dB at a point P associated with a length element dl of a wire carrying a steady current I is given by
dB = 
Question 5: What do we mean by circular current loop?
Answer:
Any circular loop is made by coiling small straight wires large number of times. This circular coil produces magnetic field when current flows through these wires. The magnetic field lines produced are straight and are perpendicular to the plane of the coil.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...