Magic Square | Even Order

A magic square of order n is an arrangement of n^2 numbers, usually distinct integers, in a square, such that the n numbers in all rows, all columns, and both diagonals sum to the same constant. A magic square contains the integers from 1 to n^2.
The constant sum in every row, column and diagonal is called the magic constant or magic sum, M. The magic constant of a normal magic square depends only on n and has the following value: 
M = n (n^2 + 1) / 2.
Examples:

Magic Square of order 3:
-----------------------
 2   7   6
 9   5   1
 4   3   8

Magic Square of order 4:
-----------------------
16 2 3 13 
5 11 10 8 
9  7 6 12 
4 14 15 1 

Magic Square of order 8:
-----------------------
64 63  3  4  5  6 58 57 
56 55 11 12 13 14 50 49 
17 18 46 45 44 43 23 24 
25 26 38 37 36 35 31 32 
33 34 30 29 28 27 39 40 
41 42 22 21 20 19 47 48 
16 15 51 52 53 54 10 9 
8  7  59 60 61 62 2  1 

A bit of Theory:
Magic squares are divided into three major categories depending upon order of square. 
1) Odd order Magic Square. Example: 3,5,7,… (2*n +1) 
2) Doubly-even order Magic Square. Example : 4,8,12,16,.. (4*n) 
3) Singly-even order Magic Square. Example : 6,10,14,18,..(4*n +2)

Algorithm for Doubly-even Magic Square :

    define an 2-D array of order n*n
    // fill array with their index-counting 
    // starting from 1
    for ( i = 0; i<n; i++)
    {
        for ( j = 0; j<n; j++)
            // filling array with its count value 
            // starting from 1;
            arr[i][j] = (n*i) + j + 1;        
    }

    // change value of Array elements 
    // at fix location as per rule 
    // (n*n+1)-arr[i][j]
    // Top Left corner of Matrix 
   // (order (n/4)*(n/4))
    for ( i = 0; i<n/4; i++)
    {
        for ( j = 0; j<n/4; j++)
            arr[i][j] = (n*n + 1) - arr[i][j];
    }

    // Top Right corner of Matrix 
    // (order (n/4)*(n/4))
    for ( i = 0; i< n/4; i++)
    {
        for ( j = 3* (n/4); j<n; j++)
            arr[i][j] = (n*n + 1) - arr[i][j];
    }

    // Bottom Left corner of Matrix 
    // (order (n/4)*(n/4))
    for ( i = 3* n/4; i<n; i++)
    {
        for ( j = 0; j<n/4; j++)
            arr[i][j] = (n*n + 1) - arr[i][j];
    }
 
    // Bottom Right corner of Matrix 
   // (order (n/4)*(n/4))
    for ( i = 3* n/4; i<n; i++)
    {
        for ( j = 3* n/4; j<n; j++)
            arr[i][j] = (n*n + 1) - arr[i][j];
    }
 
    // Centre of Matrix (order (n/2)*(n/2))
    for ( i = n/4; i<3* n/4; i++)
    {
        for ( j = n/4; j<3* n/4; j++)
            arr[i][j] = (n*n + 1) - arr[i][j];
    } 
 

Explanation with an example:(order 4)
1) Define array of order 4*4 and fill it with its count value as: 

2) Change value of top-left corner matrix of order (1*1): 

3) Change value of top-right corner matrix of order (1*1): 

4) Change value of bottom-left corner matrix of order (1*1): 

5) Change value of bottom-right corner matrix of order (1*1): 

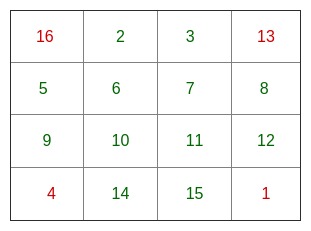
6) Change value of centre matrix of order (2*2): 

Implementation for Doubly-even Magic Square:

C++

// C++ Program to print Magic square
// of Doubly even order
#include<iostream>
using namespace std;

// Function for calculating Magic square
void doublyEven( int n )
{
    int arr[n][n], i, j;

    // filling matrix with its count value
    // starting from 1;
    for ( i = 0; i < n; i++)
        for ( j = 0; j < n; j++)
            arr[i][j] = (n*i) + j + 1;

    // change value of Array elements
    // at fix location as per rule
    // (n*n+1)-arr[i][j]
    // Top Left corner of Matrix
    // (order (n/4)*(n/4))
    for ( i = 0; i < n/4; i++)
        for ( j = 0; j < n/4; j++)
            arr[i][j] = (n*n + 1) - arr[i][j];

    // Top Right corner of Matrix
    // (order (n/4)*(n/4))
    for ( i = 0; i < n/4; i++)
        for ( j = 3 * (n/4); j < n; j++)
            arr[i][j] = (n*n + 1) - arr[i][j];

    // Bottom Left corner of Matrix
    // (order (n/4)*(n/4))
    for ( i = 3 * n/4; i < n; i++)
        for ( j = 0; j < n/4; j++)
            arr[i][j] = (n*n+1) - arr[i][j];

    // Bottom Right corner of Matrix
    // (order (n/4)*(n/4))
    for ( i = 3 * n/4; i < n; i++)
        for ( j = 3 * n/4; j < n; j++)
            arr[i][j] = (n*n + 1) - arr[i][j];

    // Centre of Matrix (order (n/2)*(n/2))
    for ( i = n/4; i < 3 * n/4; i++)
        for ( j = n/4; j < 3 * n/4; j++)
            arr[i][j] = (n*n + 1) - arr[i][j];

    // Printing the magic-square
    for (i = 0; i < n; i++)
    {
        for ( j = 0; j < n; j++)
            cout << arr[i][j] << " ";
        cout << "\n";
    }
}

// driver program
int main()
{
    int n=8;
    doublyEven(n); //Function call
    return 0;
}

Java

// Java program to print Magic square
// of Doubly even order
import java.io.*;

class GFG
{
    // Function for calculating Magic square
    static void doublyEven(int n)
    {
        int[][] arr = new int[n][n];
        int i, j;

        // filling matrix with its count value
        // starting from 1;
        for ( i = 0; i < n; i++)
            for ( j = 0; j < n; j++)
                arr[i][j] = (n*i) + j + 1;

        // change value of Array elements
        // at fix location as per rule
        // (n*n+1)-arr[i][j]
        // Top Left corner of Matrix
        // (order (n/4)*(n/4))
        for ( i = 0; i < n/4; i++)
            for ( j = 0; j < n/4; j++)
                arr[i][j] = (n*n + 1) - arr[i][j];

        // Top Right corner of Matrix
        // (order (n/4)*(n/4))
        for ( i = 0; i < n/4; i++)
            for ( j = 3 * (n/4); j < n; j++)
                arr[i][j] = (n*n + 1) - arr[i][j];

        // Bottom Left corner of Matrix
        // (order (n/4)*(n/4))
        for ( i = 3 * n/4; i < n; i++)
            for ( j = 0; j < n/4; j++)
                arr[i][j] = (n*n+1) - arr[i][j];

        // Bottom Right corner of Matrix
        // (order (n/4)*(n/4))
        for ( i = 3 * n/4; i < n; i++)
            for ( j = 3 * n/4; j < n; j++)
                arr[i][j] = (n*n + 1) - arr[i][j];

        // Centre of Matrix (order (n/2)*(n/2))
        for ( i = n/4; i < 3 * n/4; i++)
            for ( j = n/4; j < 3 * n/4; j++)
                arr[i][j] = (n*n + 1) - arr[i][j];

        // Printing the magic-square
        for (i = 0; i < n; i++)
        {
            for ( j = 0; j < n; j++)
                System.out.print(arr[i][j]+" ");
            System.out.println();
        }
    }

    // driver program
    public static void main (String[] args)
    {
        int n = 8;
        // Function call
        doublyEven(n);
    }
}

// Contributed by Pramod Kumar

Python3

# Python program to print magic square of double order

def DoublyEven(n):

    # 2-D matrix with all entries as 0
    arr = [[(n*y)+x+1 for x in range(n)]for y in range(n)]

    # Change value of array elements at fix location
    # as per the rule (n*n+1)-arr[i][[j]

    # Corners of order (n/4)*(n/4)
    # Top left corner
    for i in range(0,n//4):
        for j in range(0,n//4):
            arr[i][j] = (n*n + 1) - arr[i][j];

    # Top right corner
    for i in range(0,n//4):
        for j in range(3 * (n//4),n):
            arr[i][j] = (n*n + 1) - arr[i][j];

    # Bottom Left corner
    for i in range(3 * (n//4),n):
        for j in range(0,n//4):
            arr[i][j] = (n*n + 1) - arr[i][j];

    # Bottom Right corner
    for i in range(3 * (n//4),n):
        for j in range(3 * (n//4),n):
            arr[i][j] = (n*n + 1) - arr[i][j];

    # Centre of matrix,order (n/2)*(n/2)
    for i in range(n//4,3 * (n//4)):
        for j in range(n//4,3 * (n//4)):
            arr[i][j] = (n*n + 1) - arr[i][j];

    # Printing the square
    for i in range(n):
        for j in range(n):
            print ('%2d ' %(arr[i][j]),end=" ")
        print()

# Driver Program
n = 8
DoublyEven(n)

# Contributed by Harshit Agrawal

C#

// C# program to print Magic square
// of Doubly even order
using System;

class GFG
{
// Function for calculating Magic square
public static void doublyEven(int n)
{

    int[,] arr = new int[n,n];
    int i, j;

    // filling matrix with its count
    // value starting from 1;
    for (i = 0; i < n; i++)
    {
        for (j = 0; j < n; j++)
        {
            arr[i, j] = (n * i) + j + 1;
        }
    }

    // change value of Array elements
    // at fix location as per rule
    // (n*n+1)-arr[i][j]
    // Top Left corner of Matrix
    // (order (n/4)*(n/4))
    for (i = 0; i < n / 4; i++)
    {
        for (j = 0; j < n / 4; j++)
        {
            arr[i, j] = (n * n + 1) - arr[i, j];
        }
    }

    // Top Right corner of Matrix
    // (order (n/4)*(n/4))
    for (i = 0; i < n / 4; i++)
    {
        for (j = 3 * (n / 4); j < n; j++)
        {
            arr[i, j] = (n * n + 1) - arr[i, j];
        }
    }

    // Bottom Left corner of Matrix
    // (order (n/4)*(n/4))
    for (i = 3 * n / 4; i < n; i++)
    {
        for (j = 0; j < n / 4; j++)
        {
            arr[i, j] = (n * n + 1) - arr[i, j];
        }
    }

    // Bottom Right corner of Matrix
    // (order (n/4)*(n/4))
    for (i = 3 * n / 4; i < n; i++)
    {
        for (j = 3 * n / 4; j < n; j++)
        {
            arr[i, j] = (n * n + 1) - arr[i, j];
        }
    }

    // Centre of Matrix (order (n/2)*(n/2))
    for (i = n / 4; i < 3 * n / 4; i++)
    {
        for (j = n / 4; j < 3 * n / 4; j++)
        {
            arr[i, j] = (n * n + 1) - arr[i, j];
        }
    }

    // Printing the magic-square
    for (i = 0; i < n; i++)
    {
        for (j = 0; j < n; j++)
        {
            Console.Write(arr[i, j] + " " + " ");
        }
        Console.WriteLine();
    }
}

// Driver Code
public static void Main(string[] args)
{
    int n = 8;

    // Function call
    doublyEven(n);
}
}

// This code is contributed by Shrikant13

PHP

<?php
// PHP Program to print Magic square
// of Doubly even order

// Function for calculating Magic square
function doublyEven($n)
{
    $arr = array_fill(0, $n,
           array_fill(0, $n, 0));

    // filling matrix with its count
    // value starting from 1;
    for ( $i = 0; $i < $n; $i++)
        for ( $j = 0; $j < $n; $j++)
            $arr[$i][$j] = ($n * $i) + $j + 1;

    // change value of Array elements at fix
    // location as per rule (n*n+1)-arr[i][j]
    // Top Left corner of Matrix
    // (order (n/4)*(n/4))
    for ($i = 0; $i < $n / 4; $i++)
        for ($j = 0; $j < $n / 4; $j++)
            $arr[$i][$j] = ($n * $n + 1) -
                            $arr[$i][$j];

    // Top Right corner of Matrix
    // (order (n/4)*(n/4))
    for ($i = 0; $i < $n / 4; $i++)
        for ($j = 3 * ($n / 4); $j < $n; $j++)
            $arr[$i][$j] = ($n * $n + 1) -
                            $arr[$i][$j];

    // Bottom Left corner of Matrix
    // (order (n/4)*(n/4))
    for ($i = 3 * $n / 4; $i < $n; $i++)
        for ($j = 0; $j < $n / 4; $j++)
            $arr[$i][$j] = ($n * $n + 1) -
                            $arr[$i][$j];

    // Bottom Right corner of Matrix
    // (order (n/4)*(n/4))
    for ($i = 3 * $n / 4; $i < $n; $i++)
        for ($j = 3 * $n / 4; $j < $n; $j++)
            $arr[$i][$j] = ($n * $n + 1) -
                            $arr[$i][$j];

    // Centre of Matrix (order (n/2)*(n/2))
    for ($i = $n / 4; $i < 3 * $n / 4; $i++)
        for ($j = $n / 4; $j < 3 * $n / 4; $j++)
            $arr[$i][$j] = ($n * $n + 1) -
                            $arr[$i][$j];

    // Printing the magic-square
    for ($i = 0; $i < $n; $i++)
    {
        for ($j = 0; $j < $n; $j++)
            echo $arr[$i][$j] . " ";
        echo "\n";
    }
}

// Driver Code
$n = 8;
doublyEven($n); //Function call

// This code is contributed by mits
?>

Javascript

<script>

// javascript program to print Magic square
// of Doubly even order

// Function for calculating Magic square
    function doublyEven(n)
    {
        var arr = Array(n).fill(0).map(x => Array(n).fill(0));
        var i, j;

        // filling matrix with its count value
    // starting from 1;
    for ( i = 0; i < n; i++)
        for ( j = 0; j < n; j++)
            arr[i][j] = (n*i) + j + 1;

    // change value of Array elements
    // at fix location as per rule
    // (n*n+1)-arr[i][j]
    // Top Left corner of Matrix
    // (order (parseInt(n/4))*(parseInt(n/4)))
    for ( i = 0; i < parseInt(n/4); i++)
        for ( j = 0; j < parseInt(n/4); j++)
            arr[i][j] = (n*n + 1) - arr[i][j];

    // Top Right corner of Matrix
    // (order (parseInt(n/4))*(parseInt(n/4)))
    for ( i = 0; i < parseInt(n/4); i++)
        for ( j = 3 * (parseInt(n/4)); j < n; j++)
            arr[i][j] = (n*n + 1) - arr[i][j];

    // Bottom Left corner of Matrix
    // (order (parseInt(n/4))*(parseInt(n/4)))
    for ( i = 3 * parseInt(n/4); i < n; i++)
        for ( j = 0; j < parseInt(n/4); j++)
            arr[i][j] = (n*n+1) - arr[i][j];

    // Bottom Right corner of Matrix
    // (order (parseInt(n/4))*(parseInt(n/4)))
        for ( i = 3 * parseInt(n/4); i < n; i++)
            for ( j = 3 * parseInt(n/4); j < n; j++)
                arr[i][j] = (n*n + 1) - arr[i][j];

        // Centre of Matrix (order (n/2)*(n/2))
        for ( i = parseInt(n/4); i < 3 * parseInt(n/4); i++)
            for ( j = parseInt(n/4); j < 3 * parseInt(n/4); j++)
                arr[i][j] = (n*n + 1) - arr[i][j];

        // Printing the magic-square
    for (i = 0; i < n; i++)
    {
        for ( j = 0; j < n; j++)
            document.write(arr[i][j]+"  ");
        document.write('<br>');
    }
}

// driver program
var n = 8;
// Function call
doublyEven(n);

// This code is contributed by Amit Katiyar
</script>

Output:

64   63   3    4    5    6    58   57   
56   55   11   12   13   14   50   49   
17   18   46   45   44   43   23   24   
25   26   38   37   36   35   31   32   
33   34   30   29   28   27   39   40   
41   42   22   21   20   19   47   48   
16   15   51   52   53   54   10   9   
8    7    59   60   61   62   2   1 

Time complexity : O(n²)
Auxiliary Space: O(n²). since n² extra space has been taken.

Reference: http://www.1728.org/magicsq2.html
This article is contributed by Shivam Pradhan (anuj_charm). If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.