m-WAY Search Trees | Set-1 ( Searching )

The m-way search trees are multi-way trees which are generalised versions of binary trees where each node contains multiple elements. In an m-Way tree of order m, each node contains a maximum of m – 1 elements and m children.
The goal of m-Way search tree of height h calls for O(h) no. of accesses for an insert/delete/retrieval operation. Hence, it ensures that the height h is close to log_m(n + 1).
The number of elements in an m-Way search tree of height h ranges from a minimum of h to a maximum of .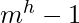
An m-Way search tree of n elements ranges from a minimum height of log_m(n+1) to a maximum of n
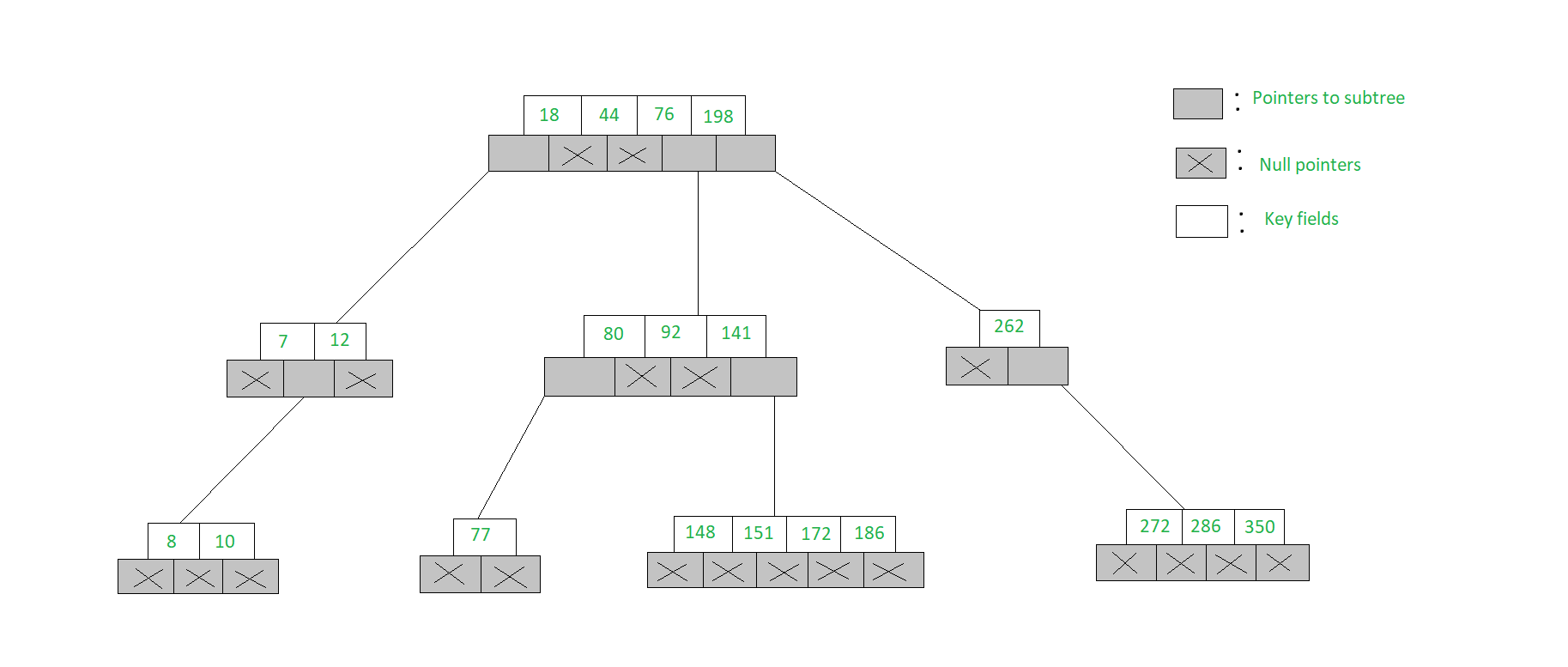
An example of a 5-Way search tree is shown in the figure below. Observe how each node has at most 5 child nodes & therefore has at most 4 keys contained in it. 

The structure of a node of an m-Way tree is given below: 

C++

struct node {
    int count;
    int value[MAX + 1];
    struct node* child[MAX + 1];
};

Java

public class Node {
    int count;
    int[] value = new int[MAX + 1];
    Node[] child = new Node[MAX + 1];
}

// This code is contributed by tapeshdua420.

Python3

class node:
    def __init__(self):
        self.count = -1
        self.value = [-1]*(MAX + 1)
        self.child = [None]*(MAX + 1)

C#

class node {
    public int count;
    public int[] value = new int[MAX + 1];
    public node[] child = new node[MAX + 1];
}

// This code is contributed by Tapesh (tapeshdua420)

Javascript

class Node {
  constructor() {
    this.count = 0;
    this.value = new Array(MAX + 1);
    this.child = new Array(MAX + 1);
  }
}

• Here, count represents the number of children that a particular node has
• The values of a node stored in the array value
• The addresses of child nodes are stored in the child array
• The MAX macro signifies the maximum number of values that a particular node can contain

Searching in an m-Way search tree:

• Searching for a key in an m-Way search tree is similar to that of binary search tree
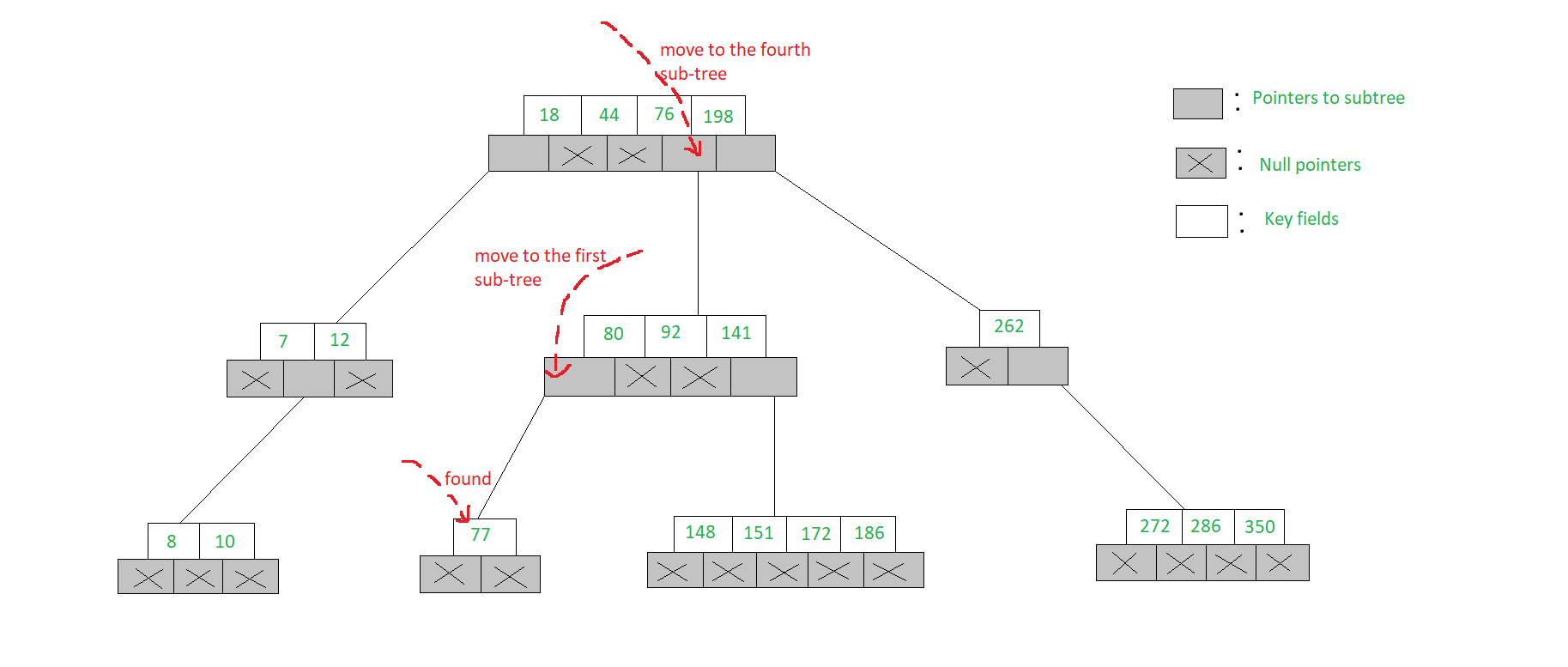
• To search for 77 in the 5-Way search tree, shown in the figure, we begin at the root & as 77> 76> 44> 18, move to the fourth sub-tree
• In the root node of the fourth sub-tree, 77< 80 & therefore we move to the first sub-tree of the node. Since 77 is available in the only node of this sub-tree, we claim 77 was successfully searched

C++

// Searches value in the node
struct node* search(int val,
                    struct node* root,
                    int* pos)
{

    // if root is Null then return
    if (root == NULL)
        return NULL;
    else {

        // if node is found
        if (searchnode(val, root, pos))
            return root;

        // if not then search in child nodes
        else
            return search(val,
                          root->child[*pos],
                          pos);
    }
}

// Searches the node
int searchnode(int val,
               struct node* n,
               int* pos)
{
    // if val is less than node->value[1]
    if (val < n->value[1]) {
        *pos = 0;
        return 0;
    }

    // if the val is greater
    else {
        *pos = n->count;

        // check in the child array
        // for correct position
        while ((val < n->value[*pos])
               && *pos > 1)
            (*pos)--;
        if (val == n->value[*pos])
            return 1;
        else
            return 0;
    }
}

Java

// Searches value in the node
public Node search(int val, Node root, int pos) {
    // if root is Null then return
    if (root == null)
        return null;
    else {
        // if node is found
        if (searchnode(val, root, pos))
            return root;

        // if not then search in child nodes
        else
            return search(val, root.child[pos], pos);
    }
}

// Searches the node
public boolean searchnode(int val, Node n, int pos) {
    // if val is less than node.value[1]
    if (val < n.value[1]) {
        pos = 0;
        return false;
    }
     // if the val is greater
    else {
        pos = n.count;

        // check in the child array
        // for correct position
        while ((val < n.value[pos]) && pos > 1)
            pos--;

        if (val == n.value[pos])
            return true;
        else
            return false;
    }
}

// This code is contributed by Tapesh(tapeshdua420)

Python3

# Searches value in the node
def search(val, root, pos):

    # if root is None then return
    if (root == None):
        return None
    else :
        # if node is found
        if (searchnode(val, root, pos)):
            return root

        # if not then search in child nodes
        else:
            return search(val, root.child[pos], pos)



# Searches the node
def searchnode(val, n, pos):
    # if val is less than node.value[1]
    if (val < n.value[1]):
        pos = 0
        return 0


    # if the val is greater
    else :
        pos = n.count

        # check in the child array
        # for correct position
        while ((val < n.value[pos]) and pos > 1):
            pos-=1
        if (val == n.value[pos]):
            return 1
        else:
            return 0

C#

// Searches value in the node
public Node search(int val, Node root, int pos)
{
    // if root is Null then return
    if (root == null)
        return null;
    else {
        // if node is found
        if (searchnode(val, root, pos))
            return root;

        // if not then search in child nodes
        else
            return search(val, root.child[pos], pos);
    }
}

// Searches the node
public bool searchnode(int val, Node n, int pos)
{
    // if val is less than node.value[1]
    if (val < n.value[1]) {
        pos = 0;
        return false;
    }

    // if the val is greater
    else {
        pos = n.count;

        // check in the child array
        // for correct position
        while ((val < n.value[pos]) && pos > 1)
            pos--;

        if (val == n.value[pos])
            return true;
        else
            return false;
    }
}

// This code is contributed by Tapesh (tapeshdua420)

Javascript

function search(val, root, pos) {
  // if root is null then return
  if (root === null) {
    return null;
  } else {
    // if node is found
    if (searchNode(val, root, pos)) {
      return root;
    }
    // if not then search in child nodes
    else {
      return search(val, root.child[pos.value], pos);
    }
  }
}

function searchNode(val, n, pos) {
  // if val is less than node.value[1]
  if (val < n.value[1]) {
    pos.value = 0;
    return false;
  }
  // if the val is greater
  else {
    pos.value = n.count;
    // check in the child array
    // for correct position
    while (val < n.value[pos.value] && pos.value > 1) {
      pos.value--;
    }
    if (val === n.value[pos.value]) {
      return true;
    } else {
      return false;
    }
  }
}

search(): 

• The function search() receives three parameters
• The first parameter is the value to be searched, second is the address of the node from where the search is to be performed and third is the address of a variable that is used to store the position of the value once found
• Initially a condition is checked whether the address of the node being searched is NULL
• If it is, then simply a NULL value is returned
• Otherwise, a function searchnode() is called which actually searches the given value
• If the search is successful the address of the node in which the value is found is returned
• If the search is unsuccessful then a recursive call is made to the search() function for the child of the current node

searchnode(): 

• The function searchnode() receives three parameters
• The first parameter is the value that is to be searched
• The second parameter is the address of the node in which the search is to be performed and third is a pointer pos that holds the address of a variable in which the position of the value that once found is stored
• This function returns a value 0 if the search is unsuccessful and 1 if it is successful
• In this function initially it is checked whether the value that is to be searched is less than the very first value of the node
• If it is then it indicates that the value is not present in the current node. Hence, a value 0 is assigned in the variable that is pointed to by pos and 0 is returned, as the search is unsuccessful