Lucas Numbers
Last Updated :
11 Sep, 2023
Lucas numbers are similar to Fibonacci numbers. Lucas numbers are also defined as the sum of its two immediately previous terms. But here the first two terms are 2 and 1 whereas in Fibonacci numbers the first two terms are 0 and 1 respectively.
Mathematically, Lucas Numbers may be defined as:
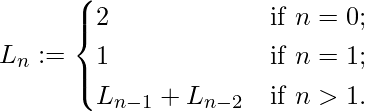
The Lucas numbers are in the following integer sequence:
2, 1, 3, 4, 7, 11, 18, 29, 47, 76, 123 …………..
Write a function int lucas(int n) n as an argument and returns the nth Lucas number.
Examples :
Input : 3
Output : 4
Input : 7
Output : 29
Method 1 (Recursive Solution)
Below is a recursive implementation based on a simple recursive formula.
C++
#include <stdio.h>
int lucas(int n)
{
if (n == 0)
return 2;
if (n == 1)
return 1;
return lucas(n - 1) +
lucas(n - 2);
}
int main()
{
int n = 9;
printf("%d", lucas(n));
return 0;
}
|
Java
class GFG
{
public static int lucas(int n)
{
if (n == 0)
return 2;
if (n == 1)
return 1;
return lucas(n - 1) +
lucas(n - 2);
}
public static void main(String args[])
{
int n = 9;
System.out.println(lucas(n));
}
}
|
Python3
def lucas(n):
if n == 0:
return 2;
if n == 1:
return 1;
return lucas(n - 1) + lucas(n - 2);
n = 9;
print(lucas(n));
|
C#
using System;
class GFG {
public static int lucas(int n)
{
if (n == 0)
return 2;
if (n == 1)
return 1;
return lucas(n - 1) + lucas(n - 2);
}
public static void Main()
{
int n = 9;
Console.WriteLine(lucas(n));
}
}
|
PHP
<?php
function lucas($n)
{
if ($n == 0)
return 2;
if ($n == 1)
return 1;
return lucas($n - 1) +
lucas($n - 2);
}
$n = 9;
echo lucas($n);
?>
|
Javascript
<script>
function lucas(n)
{
if (n == 0)
return 2;
if (n == 1)
return 1;
return lucas(n - 1) +
lucas(n - 2);
}
let n = 9;
document.write(lucas(n));
</script>
|
Output :
76
Method 2 (Iterative Solution)
The time complexity of the above implementation is exponential. We can optimize it to work in O(n) time using iteration.
C++
#include <stdio.h>
int lucas(int n)
{
int a = 2, b = 1, c, i;
if (n == 0)
return a;
for (i = 2; i <= n; i++)
{
c = a + b;
a = b;
b = c;
}
return b;
}
int main()
{
int n = 9;
printf("%d", lucas(n));
return 0;
}
|
Java
class GFG
{
static int lucas(int n)
{
int a = 2, b = 1, c, i;
if (n == 0)
return a;
for (i = 2; i <= n; i++)
{
c = a + b;
a = b;
b = c;
}
return b;
}
public static void main(String args[])
{
int n = 9;
System.out.println(lucas(n));
}
}
|
Python3
def lucas(n) :
a = 2
b = 1
if (n == 0) :
return a
for i in range(2, n + 1) :
c = a + b
a = b
b = c
return b
n = 9
print(lucas(n))
|
C#
using System;
class GFG {
static int lucas(int n)
{
int a = 2, b = 1, c, i;
if (n == 0)
return a;
for (i = 2; i <= n; i++) {
c = a + b;
a = b;
b = c;
}
return b;
}
public static void Main()
{
int n = 9;
Console.WriteLine(lucas(n));
}
}
|
PHP
<?php
function lucas($n)
{
$a = 2; $b = 1; $c; $i;
if ($n == 0)
return $a;
for ($i = 2; $i <= $n; $i++)
{
$c = $a + $b;
$a = $b;
$b = $c;
}
return $b;
}
$n = 9;
echo lucas($n);
?>
|
Javascript
<script>
function lucas(n)
{
let a = 2, b = 1, c, i;
if (n == 0)
return a;
for (i = 2; i <= n; i++) {
c = a + b;
a = b;
b = c;
}
return b;
}
let n = 9;
document.write(lucas(n));
</script>
|
Output :
76
Time complexity: O(n) since using a for loop
Space complexity: O(1) since using constant variables, since no extra space has been taken.
References:
https://en.wikipedia.org/wiki/Lucas_number
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...