Longest Common Prefix using Character by Character Matching
Last Updated :
10 Feb, 2023
Given a set of strings, find the longest common prefix.
Input : {“geeksforgeeks”, “geeks”, “geek”, “geezer”}
Output : "gee"
Input : {"apple", "ape", "april"}
Output : "ap"
We have discussed word by word matching algorithm in previous post.
In this algorithm, instead of going through the strings one by one, we will go through the characters one by one.
We consider our strings as – “geeksforgeeks”, “geeks”, “geek”, “geezer”.

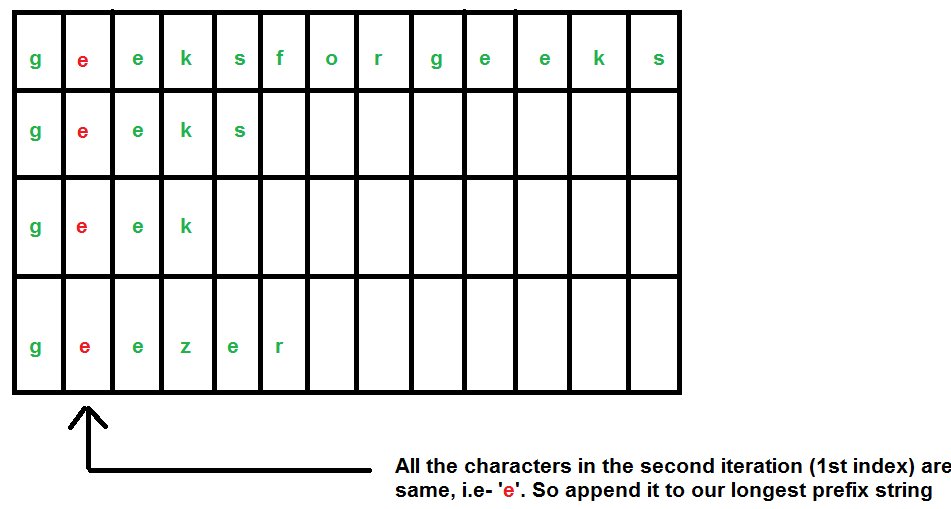


Below is the implementation of this approach.
C++
#include<bits/stdc++.h>
using namespace std;
int findMinLength(string arr[], int n)
{
int min = arr[0].length();
for (int i=1; i<n; i++)
if (arr[i].length() < min)
min = arr[i].length();
return(min);
}
string commonPrefix(string arr[], int n)
{
int minlen = findMinLength(arr, n);
string result;
char current;
for (int i=0; i<minlen; i++)
{
current = arr[0][i];
for (int j=1 ; j<n; j++)
if (arr[j][i] != current)
return result;
result.push_back(current);
}
return (result);
}
int main()
{
string arr[] = {"geeksforgeeks", "geeks",
"geek", "geezer"};
int n = sizeof (arr) / sizeof (arr[0]);
string ans = commonPrefix (arr, n);
if (ans.length())
cout << "The longest common prefix is "
<< ans;
else
cout << "There is no common prefix";
return (0);
}
|
Java
class GFG
{
static int findMinLength(String arr[], int n)
{
int min = arr[0].length();
for (int i = 1; i < n; i++)
{
if (arr[i].length() < min)
{
min = arr[i].length();
}
}
return (min);
}
static String commonPrefix(String arr[], int n)
{
int minlen = findMinLength(arr, n);
String result = "";
char current;
for (int i = 0; i < minlen; i++)
{
current = arr[0].charAt(i);
for (int j = 1; j < n; j++)
{
if (arr[j].charAt(i) != current)
{
return result;
}
}
result += (current);
}
return (result);
}
public static void main(String[] args)
{
String arr[] = {"geeksforgeeks", "geeks",
"geek", "geezer"};
int n = arr.length;
String ans = commonPrefix(arr, n);
if (ans.length() > 0) {
System.out.println("The longest common prefix is "
+ ans);
} else {
System.out.println("There is no common prefix");
}
}
}
|
Python 3
def findMinLength(arr, n):
min = len(arr[0])
for i in range(1,n):
if (len(arr[i])< min):
min = len(arr[i])
return(min)
def commonPrefix(arr, n):
minlen = findMinLength(arr, n)
result =""
for i in range(minlen):
current = arr[0][i]
for j in range(1,n):
if (arr[j][i] != current):
return result
result = result+current
return (result)
if __name__ == "__main__":
arr = ["geeksforgeeks", "geeks",
"geek", "geezer"]
n = len(arr)
ans = commonPrefix (arr, n)
if (len(ans)):
print("The longest common prefix is ",ans)
else:
print("There is no common prefix")
|
C#
using System;
class GFG
{
static int findMinLength(String []arr, int n)
{
int min = arr[0].Length;
for (int i = 1; i < n; i++)
{
if (arr[i].Length < min)
{
min = arr[i].Length;
}
}
return (min);
}
static String commonPrefix(String []arr, int n)
{
int minlen = findMinLength(arr, n);
String result = "";
char current;
for (int i = 0; i < minlen; i++)
{
current = arr[0][i];
for (int j = 1; j < n; j++)
{
if (arr[j][i] != current)
{
return result;
}
}
result += (current);
}
return (result);
}
public static void Main(String[] args)
{
String []arr = {"geeksforgeeks", "geeks",
"geek", "geezer"};
int n = arr.Length;
String ans = commonPrefix(arr, n);
if (ans.Length > 0)
{
Console.WriteLine("The longest common prefix is "
+ ans);
}
else
{
Console.WriteLine("There is no common prefix");
}
}
}
|
Javascript
<script>
function findMinLength(arr,n)
{
let min = arr[0].length;
for (let i = 1; i < n; i++)
{
if (arr[i].length < min)
{
min = arr[i].length;
}
}
return (min);
}
function commonPrefix(arr,n)
{
let minlen = findMinLength(arr, n);
let result = "";
let current;
for (let i = 0; i < minlen; i++)
{
current = arr[0][i];
for (let j = 1; j < n; j++)
{
if (arr[j][i] != current)
{
return result;
}
}
result += (current);
}
return (result);
}
let arr=["geeksforgeeks", "geeks",
"geek", "geezer"]
let n = arr.length;
let ans = commonPrefix(arr, n);
if (ans.length > 0) {
document.write("The longest common prefix is "
+ ans);
} else {
document.write("There is no common prefix");
}
</script>
|
Output
The longest common prefix is gee
How is this algorithm better than the “Word by Word Matching” algorithm ?-
In Set 1 we discussed about the “Word by Word Matching” Algorithm.
Suppose you have the input strings as- “geeksforgeeks”, “geeks”, “geek”, “geezer”, “x”.
Now there is no common prefix string of the above strings. By the “Word by Word Matching” algorithm discussed in Set 1, we come to the conclusion that there is no common prefix string by traversing all the strings. But if we use this algorithm, then in the first iteration itself we will come to know that there is no common prefix string, as we don’t go further to look for the second character of each strings.
This algorithm has a huge advantage when there are too many strings.
Time Complexity : Since we are iterating through all the characters of all the strings, so we can say that the time complexity is O(N M) where,
N = Number of strings
M = Length of the Smallest string
Auxiliary Space : To store the longest prefix string we are allocating space which is O(M).
Method 3(using some in-built C++ STL function):
In this approach first of all we will find the string with smallest length. Then we will search in all other strings if this smallest string is present in them as a prefix or not. If in all strings this small string is present is present then we will print this string else we will keep reducing the length of the smallest string by one until its length becomes zero.
Below is the implementation of the above Approach:
Implementation:
C++
#include <bits/stdc++.h>
using namespace std;
int shortest_string(string s[], int n)
{
int minlength = INT_MAX, min_index;
for (int i = 0; i < n; i++) {
if (s[i].length() < minlength) {
minlength = s[i].length();
min_index = i;
}
}
return min_index;
}
string findprefix(string s[], int n)
{
int shortest_string_index = shortest_string(s, n);
while (s[shortest_string_index].length() > 0) {
int count = 0;
for (int i = 0; i < n; i++) {
if (s[i].find(s[shortest_string_index]) == 0) {
count++;
}
}
if (count == n) {
cout << "longest common prefix is: " << endl;
return s[shortest_string_index];
break;
}
s[shortest_string_index].pop_back();
}
return "no common prefix among all strings";
}
int main()
{
string s[]
= { "geeksforgeeks", "geeks", "geek", "geezer" };
int n = sizeof(s) / sizeof(s[0]);
cout << findprefix(s, n);
return 0;
}
|
Java
import java.io.*;
class GFG {
static int shortest_string(String s[], int n)
{
int minlength = Integer.MAX_VALUE, min_index = -1;
for (int i = 0; i < n; i++) {
if (s[i].length() < minlength) {
minlength = s[i].length();
min_index = i;
}
}
return min_index;
}
static String findprefix(String s[], int n)
{
int shortest_string_index = shortest_string(s, n);
while (s[shortest_string_index].length() > 0) {
int count = 0;
for (int i = 0; i < n; i++) {
if (s[i].indexOf(s[shortest_string_index]) == 0) {
count++;
}
}
if (count == n) {
System.out.println("longest common prefix is:");
return s[shortest_string_index];
}
s[shortest_string_index] = s[shortest_string_index].substring(0,s[shortest_string_index].length()-1);
}
return "no common prefix among all strings";
}
public static void main (String[] args) {
String s[] = { "geeksforgeeks", "geeks", "geek", "geezer" };
int n = s.length;
System.out.println(findprefix(s, n));
}
}
|
Python3
import sys
def shortest_string(s, n):
minlength = sys.maxsize
min_index = 0
for i in range(n):
if len(s[i]) < minlength:
minlength = len(s[i])
min_index = i
return min_index
def findprefix(s, n):
shortest_string_index = shortest_string(s, n)
while len(s[shortest_string_index]) > 0:
count = 0
for i in range(n):
if s[i].find(s[shortest_string_index]) == 0:
count += 1
if count == n:
print("longest common prefix is: ")
return s[shortest_string_index]
break
s[shortest_string_index] = s[shortest_string_index][:-1]
return "no common prefix among all strings"
s = ["geeksforgeeks", "geeks",
"geek", "geezer"]
n = len(s)
print(findprefix(s, n))
|
C#
using System;
public class GFG
{
public static int shortest_string(String[] s, int n)
{
var minlength = int.MaxValue;
var min_index = -1;
for (int i = 0; i < n; i++)
{
if (s[i].Length < minlength)
{
minlength = s[i].Length;
min_index = i;
}
}
return min_index;
}
public static String findprefix(String[] s, int n)
{
var shortest_string_index = GFG.shortest_string(s, n);
while (s[shortest_string_index].Length > 0)
{
var count = 0;
for (int i = 0; i < n; i++)
{
if (s[i].IndexOf(s[shortest_string_index]) == 0)
{
count++;
}
}
if (count == n)
{
Console.WriteLine("longest common prefix is:");
return s[shortest_string_index];
}
s[shortest_string_index] = s[shortest_string_index].Substring(0,s[shortest_string_index].Length - 1-0);
}
return "no common prefix among all strings";
}
public static void Main(String[] args)
{
String[] s = {"geeksforgeeks", "geeks", "geek", "geezer"};
var n = s.Length;
Console.WriteLine(GFG.findprefix(s, n));
}
}
|
Javascript
function shortest_string(s, n) {
let minlength = Number.MAX_SAFE_INTEGER;
let min_index;
for (let i = 0; i < n; i++) {
if (s[i].length < minlength) {
minlength = s[i].length;
min_index = i;
}
}
return min_index;
}
function findprefix(s, n) {
let shortest_string_index = shortest_string(s, n);
while (s[shortest_string_index].length > 0) {
let count = 0;
for (let i = 0; i < n; i++) {
if (s[i].indexOf(s[shortest_string_index]) === 0) {
count++;
}
}
if (count === n) {
console.log("longest common prefix is: ");
return s[shortest_string_index];
break;
}
s[shortest_string_index] = s[shortest_string_index].slice(0, -1);
}
return "no common prefix among all strings";
}
let s = ["geeksforgeeks", "geeks", "geek", "geezer"];
let n = s.length;
console.log(findprefix(s, n));
|
Output
longest common prefix is:
gee
Time complexity: O(n*m) where n is total number of strings and m is length of the smallest string among all strings.
Auxiliary space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...