Logarithmic Differentiation helps to find the derivatives of complicated functions, using the concept of logarithms. Sometimes finding the differentiation of the function is very tough but differentiating the logarithm of the same function is very easy, then in such cases, the logarithmic differentiation formula is used.
In calculus, the differentiation of some complex functions is found first by taking log and then finding the logarithmic derivative of that function. In this article, we will learn about Logarithmic Differentiation in detail.
What is Logarithmic Differentiation?
Method of finding the derivative of a function by first taking the logarithm and then differentiating is called logarithmic differentiation. This method is specially used when the function is type y = f(x)g(x). In this type of problem where y is a composite function, we first need to take a logarithm, making the function log (y) = g(x) log (f(x)). This creates a situation where the differentiation of the exponent function was quite tricky but after taking the log on both sides of the equation, we can easily differentiate it using logarithm properties and the chain rule. This method is also known as Composite exponential function differentiation. This approach allows us to calculate the derivative of complex exponential functions efficiently.
Logarithmic differentiation uses the chain rule of differentiation and is generally used to differentiate functions of form f(x)g(x), f(x)/g(x), f(x)g(x), and others.
Read More: Laws of Logarithms
Logarithmic Differentiation Formula
For a function, y = f(x)g(x), differentiation is given by the following formula:
![Rendered by QuickLaTeX.com \bold{\frac{dy}{dx} = y\left[g(x)\cdot \frac{f'(x)}{f(x)} + log(f(x))g'(x)\right]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c92a6e6e326f87e2b26153cc666af1fd_l3.png)
Logarithmic formulas are very useful in solving logarithmic differentiation. Some of the important logarithmic properties used are,
- log XY = log X + log Y
- log X/Y = log X – log Y
- log XY = Y log X
- logY X = (log X) / (log Y)
Note: Logarithmic differentiation rules are only valid for the positive functions only because logarithm of negative function is undefined.
Derivation of Logarithmic Differentiation Formula
Let us consider a function y = f(x)g(x),
and take the natural logarithm of this function to differentiate it,
ln y = ln (f(x)g(x))
⇒ ln (y) = g(x) ln (f(x))
Differentiate the above equation,
![Rendered by QuickLaTeX.com \frac{d [\ln y]}{dx} = \frac{d}{dx}[g(x) \cdot \ln f(x)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-69cd9a0b062396eec40d986af808f911_l3.png)
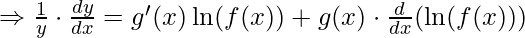
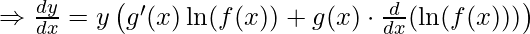
![Rendered by QuickLaTeX.com \Rightarrow \frac{dy}{dx} = y \left[g'(x) \ln(f(x)) + g(x) \cdot \frac{f'(x)}{f(x)}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-05b38728835cef7a024c9845e1ec29c3_l3.png)
Which is the required formula.
Applications of Log Differentiation
Log differentiation found its application while solving various differentiation problems. Various types of problems where Log Differentiation is used are discussed below,
Product of Functions (Product Rule)
The differentiation of any function which is a product of two functions can easily be calculated using logarithmic differentiation.
Suppose we have to find differentiation of f(x) where, f(x) = g(x) × h(x) then by using concept of logarithmic differentiation,
f(x) = g(x) × h(x)
Taking log on both sides,
log f(x) = log (g(x) × h(x))
log f(x) = log g(x) + log h(x) [Using property log (XY) = log (X) + log (Y)]
Differentiating both sides with respect to x,
d/dx [log f(x)] = d/dx [log g(x)] + d/dx [log h(x)]
f'(x)/f(x) = g'(x)/g(x) + h'(x)/h(x)
f'(x) = f(x) [g'(x)/g(x) + h'(x)/h(x)]
f'(x) = f(x) [(h(x)×g'(x) + g(x)×h'(x))/ (g(x)×h(x))]
f'(x) = g(x)×h(x) [h(x)×g'(x) + g(x)×h'(x)] / g(x)×h(x)
f'(x) = h(x)×g'(x) + g(x)×h'(x)
The result obtained above is the “Leibniz rule” and is commonly known as the “Product rule“.
Division of Functions (Quotient Rule)
The differentiation of any function which is in the form of a division of two functions can easily be calculated using logarithmic differentiation.
Suppose one has to find the differentiation of f(x) where f(x) = g(x) / h(x) by using the concept of logarithmic. differentiation,
f(x) = g(x)/h(x)
Taking log on both sides,
log f(x) = log [g(x)/h(x)]
log f(x) = log g(x) – log h(x) [Using property log (X/Y) = log (X) – log (Y)]
Differentiating both sides with respect to x,
d/dx [log f(x)] = d/dx [log g(x)] – d/dx [log h(x)]
f'(x)/f(x) = g'(x)/g(x) – h'(x)/h(x)
f'(x) = f(x)[g'(x)/g(x) – h'(x)/h(x)]
f'(x) = f(x) [(g'(x)×h(x) – g(x)×h'(x))/(g(x)×h(x))]
f'(x) = g(x)/h(x) [g'(x)×h(x) – g(x)×h'(x)]/g(x)×h(x)
f'(x) = [g'(x)×h(x) – g(x)×h'(x)] / h2(x)
The result obtained above is commonly known as the “Quotient rule“.
Exponential Functions
The differentiation of any function which is in exponential form can easily be calculated using logarithmic differentiation.
Suppose we have to find differentiation of f(x) where, f(x) = g(x)h(x) then by using concept of logarithmic differentiation,
f(x) = g(x)h(x)
Taking log on both sides
log f(x) = log [g(x)h(x)]
log f(x) = h(x) × log (g(x)) [Using property log (XY) = Ylog (X)]
Differentiating both sides with respect to x,
d/dx [log f(x)] = d/dx [h(x) × log g(x)]
f'(x)/f(x) = h(x) × d/dx log g(x) + log g(x) × d/dx h(x) [Using uv rule of differentiation]
f'(x)/f(x) = h(x) × g'(x)/g(x) + log g(x) × h'(x)
f'(x)/f(x) = [h(x) × g'(x) + g(x) × h'(x) × log g(x)] / g(x)
f'(x) = f(x) [h(x)×g'(x) + g(x)×h'(x)×log g(x)] / g(x)
f'(x) = g(x)h(x) [h(x)×g'(x) + g(x)×h'(x)×log g(x)] / g(x)
f'(x) = g(x)h(x)-1 [h(x)×g'(x) + g(x)×h'(x)×log g(x)]
Method to Solve Logarithmic Functions
The steps involved in differentiating a logarithmic function are summarized below,
- Take log on both sides,
- Use logarithmic properties to simplify the function,
- Now differentiate the equation with respect to x,
- Simplify the obtained equation,
- Substitute back the value of y.
Following the above result one can easily find the differentiation of logarithmic functions.
Also, Check
Solved Examples on Logarithmic Differentiation
Example 1: Find the derivative of xx.
Solution:
Let y = xx
Step 1: Taking log on both sides
log(y) = log(xx)
Step 2: Use logarithmic property to simplify the equation
log(y) = x ⋅ log(x) [Using property log(ab) = b⋅ log(a)]
Step 3: Now differentiate the equation with respect to x,
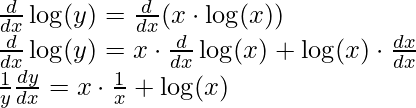
Step 4: Simplify the obtained equation
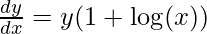
Step 5: Substitute back the value of y
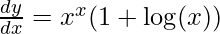
Example 2: Find the derivative of 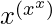 ?
?
Solution:
Given,
y = 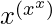
Step 1: Taking log on both sides,
log(y) = log(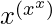 )
)
Step 2: Use logarithmic property to simplify the equation
log(y) = xx⋅ log(x) [Using property log(ab) = b⋅ log(a)]
Step 3: Differentiating both sides with respect to x,
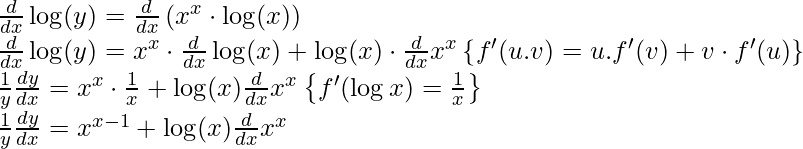
Step 4: Simplify the obtained equation,
Since now we know the derivative of xx, We will substitute here directly.
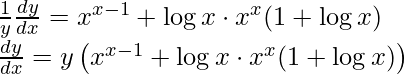
Step 5: Substitute back the value of y
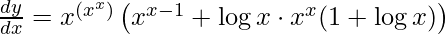
Example 3: Find the derivative of y = (log x)x.
Solution:
Given,
y = (logx)x
Step 1: Taking log on both sides,
log(y) = log((logx)x)
Step 2: Use logarithmic property to simplify the equation
log(y) = x ⋅ log(logx) [using property log(ab) = b⋅ log(a)]
Step 3: Differentiating both sides with respect to x,
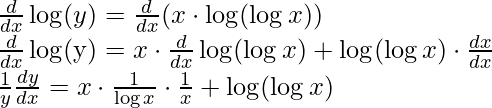
Step 4: Simplify the obtained equation,
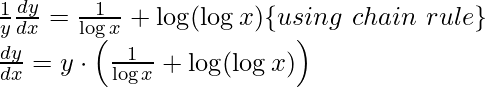
Step 5: Substitute back the value of y
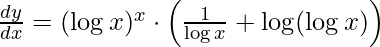
Example 4: Find the derivative of y = x√x.
Solution:
Given,
y = x√x
Step 1: Taking log on both sides,
log(y) = log(x√x)
Step 2: Use logarithmic property to simplify the equation
log(y) = √x⋅ log(x) [using property log(ab) = b⋅ log(a)]
Step 3: Differentiating both sides with respect to x,
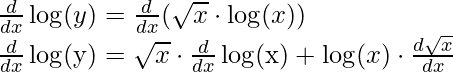
Step 4: Simplify the obtained equation,
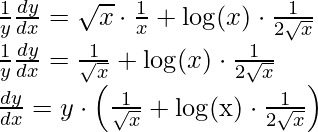
Step 5: Substitute back the value of y
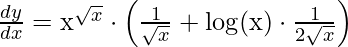
FAQs on Logarithmic Differentiation
Q1: What is the Formula of Logarithmic Differentiation?
Answer:
Logarithmic Differentiation of a function f(x) is found by dividing the differentiation of the function by the function itself. i.e.
d/dx [log f(x)] = f ‘(x)/f(x)
Logarithmic differentiation of a function is calculated using the chain rule of differentiation. These functions are also used to solve exponential functions.
Q2: When Logarithmic Differentiation is used?
Answer:
Logarithmic differentiation is used when one need to find the differentiation of the complex function, such as, multiplication or division of two fucntions, a function in power of another function, etc. Logarithmic differentiation solves such types of complex functions very easily.
Q3: What are the Examples of Log Differentiation?
Answer:
Logarithmic differentiation is used to solve different functions, such as, exponential ecos x, product (x + 5)3 (x2 + 2)3, exponent (cos x)sin x , etc.
Q4: What are the Different Rules of Logarithmic Differentiation?
Answer:
Logarithmic differentiation uses the following rules to obtain the differentiation of the complex functions, such as,
- Product Rule
- Quotient Rule
- Exponential Rule
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...