Logarithm

Difficulty Level : Medium
Last Updated : 30 Jun, 2021

Logarithmic function is the inverse to the exponential function. A logarithm to the base b is the power to which b must be raised to produce a given number. For example, 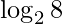$\log_2 8$ is equal to the power to which 2 must be raised to in order to produce 8. Clearly, 2^3 = 8 so 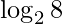$\log_2 8$ = 3. In general, for b > 0 and b not equal to 1.

Fact about Logarithm :

Logarithms were quickly adopted by scientists because of various useful properties that simplified long, tedious calculations.
Logarithm to base 10 (that is b = 10) is called the common logarithm and has many applications in science and engineering.
Natural logarithm, is a logarithm with base e. It is used in mathematics and physics, because of its simpler derivative.
Binary logarithm is a logarithm with base 2 and is commonly used in computer science.

Laws of Logarithms :

Laws	Description
* QuickLaTeX cannot compile formula: * Error message: Error: Nothing to show, formula is empty	$\log_a b$ + $\log_a c$
* QuickLaTeX cannot compile formula: * Error message: Error: Nothing to show, formula is empty	$\log_a b$ – $\log_a c$
* QuickLaTeX cannot compile formula: * Error message: Error: Nothing to show, formula is empty	$c\log_a b$
* QuickLaTeX cannot compile formula: * Error message: Error: Nothing to show, formula is empty	$-\log_a b$
* QuickLaTeX cannot compile formula: * Error message: Error: Nothing to show, formula is empty	$0$
* QuickLaTeX cannot compile formula: * Error message: Error: Nothing to show, formula is empty	$1$
* QuickLaTeX cannot compile formula: * Error message: Error: Nothing to show, formula is empty	$r$
* QuickLaTeX cannot compile formula: * Error message: Error: Nothing to show, formula is empty * * QuickLaTeX cannot compile formula: * Error message: Error: Nothing to show, formula is empty	$\log_a c$
* QuickLaTeX cannot compile formula: * Error message: Error: Nothing to show, formula is empty	$1/\log_a b$

How to find logarithm of number?
Naive solution:
The idea is to create a function that calculates and returns $\log_2 n$ . For example, if n = 64, then your function should return 6, and if n = 129, then your function should return 7.

C++

// C++ program to find log(n) using Recursion
#include <bits/stdc++.h>
using namespace std;
 
unsigned int Log2n(unsigned int n)
{
    return (n > 1) ? 1 + Log2n(n / 2) : 0;
}
 
int main()
{
    unsigned int n = 32;
    cout<< Log2n(n)<<"\n";
    return 0;
} 
 
// This code is contributed by UJJWAL BHARDWAJ

C

// C program to find log(n) using Recursion
#include <stdio.h>
 
unsigned int Log2n(unsigned int n)
{
    return (n > 1) ? 1 + Log2n(n / 2) : 0;
}
 
int main()
{
    unsigned int n = 32;
    printf("%u", Log2n(n));
    getchar();
    return 0;
}

Java

// Java program to find log(n)
// using Recursion
class Gfg1 {
 
    static int Log2n(int n)
    {
        return (n > 1) ? 1 + Log2n(n / 2) : 0;
    }
 
    // Driver Code
    public static void main(String args[])
    {
        int n = 32;
        System.out.println(Log2n(n));
    }
}

Python3

# Python 3 program to
# find log(n) using Recursion
 
def Log2n(n):
 
    return 1 + Log2n(n / 2) if (n > 1) else 0
 
# Driver code
n = 32
print(Log2n(n))

C#

// C# program to find log(n)
// using Recursion
using System;
 
class GFG {
 
    static int Log2n(int n)
    {
        return (n > 1) ? 1 + Log2n(n / 2) : 0;
    }
 
    // Driver Code
    public static void Main()
    {
        int n = 32;
 
        Console.Write(Log2n(n));
    }
}

PHP

<?php
// PHP program
// to find log(n) using Recursion
 
function Log2n($n)
{
    return ($n > 1) ? 1 + Log2n($n / 2) : 0;
}
 
// Drive main
 
    $n = 32;
    echo Log2n($n);
?>

Output :

Time complexity: O(log n)
Auxiliary space: O(log n) if the stack size is considered during recursion otherwise O(1)
Efficient solutions:

Using inbuilt log Function

Practice problems on Logarithm:

Question 1: Find the value of x in equation given 8^x+1 – 8^x-1 = 63
Solution: Take 8^x-1 common from the eq.
It reduce to
8^x-1(8² – 1) = 63
8^x-1 = 1
Hence, x – 1 = 0
x = 1
Question 2: Find the value of x for the eq. given log_0.25x = 16
Solution: log_0.25x = 16
It can be write as
x = (0.25)¹⁶
x = (1/4)¹⁶
x = 4^-16
Question 3: Solve the equation log₁₂1728 x log₉6561
Solution: It can be written as
log₁₂(12³) x log₉(9⁴)
= 3log₁₂12 x 4log₉9
= 3 x 4 = 12
Question 4: Solve for x
log_x3 + log_x9 + log_x27 + log_x81 = 10
Solution: It can be write as
log_x(3 x 9 x 27 x 81) = 10
log_x(3¹ x 3² x 3³ x 3⁴) = 10
log_x(3¹⁰) = 10
10 log_x3 = 10
then, x = 3
Question 5: If log(a + 3 ) + log(a – 3) = 1 ,then a=?
Solution: log₁₀((a + 3)(a – 3))=1
log₁₀(a² – 9) = 1
(a² – 9) = 10
a² = 19
a = √19
Question 6: Solve 1/log_ab(abcd) + 1/log_bc(abcd) + 1/log_cd(abcd) + 1/log_da(abcd)
Solution:
=log_abcd(ab) + log_abcd(bc) + log_abcd(cd) + log_abcd(da)
=log_abcd(ab * bc * cd * da)
=log_abcd(abcd)²
=2 log_abcd(abcd)
=2
Question 7: If xyz = 10 , then solve log(xⁿ yⁿ / zⁿ) + log(yⁿ zⁿ / xⁿ) + log(zⁿ xⁿ / yⁿ)
Solution:
log(xⁿ yⁿ / zⁿ * yⁿ zⁿ / xⁿ * zⁿ xⁿ / yⁿ)
= log xⁿ yⁿ zⁿ
= log(xyz)ⁿ
= log₁₀ 10ⁿ
= n
Question 8: Find (121/10)^x = 3
Solution: Apply logarithm on both sides
log_(121/10)(121/10)^x = log_(121/10)3
x = (log 3) / (log 121 – log 10)
x = (log 3) / (2 log 11 – 1)
Question 9: Solve log(2x² + 17)= log (x – 3)²
Solution:
log(2x² + 17)= log (x² – 6x + 9)
2x² + 17 = x² – 6x + 9
x² + 6x + 8 = 0
x² + 4x + 2x + 8 = 0
x(x + 4) + 2(x + 4) = 0
(x + 4)(x + 2)=0
x= -4,-2
Question 10: log₂(33 – 3^x)= 10^{log(5 – x)}. Solve for x.
Solution: Put x = 0
log₂(33 – 1)= 10^log(5)
log₂32 = 5
5 log₂ 2 = 5
5 = 5
LHS = RHS

More problems related to Logarithm :

Recent Articles on Logarithm!

Attention reader! Don’t stop learning now. Get hold of all the important mathematical concepts for competitive programming with the Essential Maths for CP Course at a student-friendly price. To complete your preparation from learning a language to DS Algo and many more, please refer Complete Interview Preparation Course.

My Personal Notes

Related Articles

Logarithm

C++

C

Java

Python3

C#

PHP

Practice problems on Logarithm: