Logarithm tricks for Competitive Programming
Last Updated :
01 Nov, 2023
Logarithm: is the inverse function of the exponentiation which means the logarithm value of a given number x is the exponent to another number.
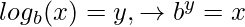
Below are some tricks using Logarithmic function which can be handy in competitive programming.
Checking if a number is a power of two or not:
Given an integer N, the task is to check that if the number N is the power of 2.
Examples:
Input: N = 8
Output: Yes
Input: N = 6
Output: No
Approach: A simple method for this is to simply take the log of the number on base 2, if you get an integer then the number is the power of 2.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
bool isPowerOfTwo(int n)
{
return (ceil(log2(n)) == floor(log2(n)));
}
int main()
{
int N = 8;
if (isPowerOfTwo(N)) {
cout << "Yes";
}
else {
cout << "No";
}
}
|
C
#include <stdio.h>
#include <math.h>
_Bool isPowerOfTwo(int n)
{
return (ceil(log2(n)) == floor(log2(n)));
}
int main()
{
int N = 8;
if (isPowerOfTwo(N))
{
printf("Yes");
}
else
{
printf("No");
}
}
|
Java
import java.lang.Math;
class GFG{
public static boolean isPowerOfTwo(int n)
{
return(Math.ceil(Math.log(n) /
Math.log(2)) ==
Math.floor(Math.log(n) /
Math.log(2)));
}
public static void main(String[] args)
{
int N = 8;
if (isPowerOfTwo(N))
{
System.out.println("Yes");
}
else
{
System.out.println("No");
}
}
}
|
Python3
import math
def isPowerOfTwo(n):
return(math.ceil(math.log(n) //
math.log(2)) ==
math.floor(math.log(n) //
math.log(2)));
if __name__=='__main__':
N = 8
if isPowerOfTwo(N):
print('Yes')
else:
print('No')
|
C#
using System;
class GFG{
public static bool isPowerOfTwo(int n)
{
return(Math.Ceiling(Math.Log(n) /
Math.Log(2)) ==
Math.Floor(Math.Log(n) /
Math.Log(2)));
}
public static void Main(String[] args)
{
int N = 8;
if (isPowerOfTwo(N))
{
Console.WriteLine("Yes");
}
else
{
Console.WriteLine("No");
}
}
}
|
Javascript
<script>
function isPowerOfTwo(n)
{
return (Math.ceil(Math.log(n) / Math.log(2)) == Math.floor(Math.log(n) / Math.log(2)));
}
let N = 8;
if (isPowerOfTwo(N)) {
document.write("Yes");
}
else {
document.write("No");
}
</script>
|
Time Complexity: O(logn)
Auxiliary Space: O(1)
Kth root of a Number
Given two integers N and K, the task is to find the Kth root of the number N.
Examples:
Input: N = 8, K = 3
Output: 2
Input: N = 32, K = 5
Output: 2
Approach: A simple solution is to use logarithmic function to find the Kth root of the number. Below is the illustration of the approach:
Let D be our answer
then, 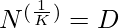
Applying 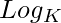 on both side
on both side
=> 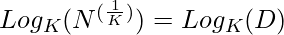
=> 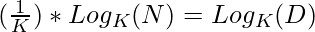
=> 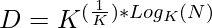
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
double kthRoot(double n, int k)
{
return pow(k,
(1.0 / k)
* (log(n)
/ log(k)));
}
int main()
{
double N = 8.0;
int K = 3;
cout << kthRoot(N, K);
return 0;
}
|
Java
class GFG{
static double kthRoot(double n, int k)
{
return Math.pow(k, (1.0 / k) *
(Math.log(n) / Math.log(k)));
}
public static void main(String[] args)
{
double N = 8.0;
int K = 3;
System.out.print(kthRoot(N, K));
}
}
|
Python3
import math
def kth_root(n, k):
return(pow(k, ((1.0 / k) * (math.log(n) /
math.log(k)))))
if __name__=="__main__":
n = 8.0
k = 3
print(round(kth_root(n, k)))
|
C#
using System;
class GFG{
static double kthRoot(double n, int k)
{
return Math.Pow(k, (1.0 / k) *
(Math.Log(n) / Math.Log(k)));
}
public static void Main()
{
double N = 8.0;
int K = 3;
Console.Write(kthRoot(N, K));
}
}
|
Javascript
<script>
function kthRoot(n, k)
{
return Math.pow(k,
(1.0 / k)
* (Math.log(n)
/ Math.log(k)));
}
var N = 8.0;
var K = 3;
document.write( kthRoot(N, K));
</script>
|
Time Complexity: O(logn)
Auxiliary Space: O(1)
Count digits in a Number:
Given an integer N, the task is to count the digits in a number N.
Examples:
Input: N = 243
Output: 3
Input: N = 1000
Output: 4
Approach: The idea is to find the logarithm of the number base 10 to count the number of digits.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int countDigit(long long n)
{
return floor(log10(n) + 1);
}
int main()
{
double N = 80;
cout << countDigit(N);
return 0;
}
|
C
#include <stdio.h>
#include <math.h>
int countDigit(long long n)
{
return (floor(log10(n) + 1));
}
int main()
{
double N = 80;
printf("%d", countDigit(N));
return 0;
}
|
Java
class GFG{
static int countDigit(double n)
{
return((int)Math.floor(Math.log10(n) + 1));
}
public static void main(String[] args)
{
double N = 80;
System.out.println(countDigit(N));
}
}
|
Python3
import math
def countDigit(n):
return(math.floor(math.log10(n) + 1))
if __name__=="__main__":
n = 80
print(countDigit(n))
|
C#
using System;
class GFG{
static int countDigit(double n)
{
return((int)Math.Floor(Math.Log10(n) + 1));
}
public static void Main()
{
double N = 80;
Console.Write(countDigit(N));
}
}
|
Javascript
<script>
function countDigit(n)
{
return Math.floor(Math.log10(n) + 1);
}
var n = 80;
document.write(countDigit(n));
</script>
|
Time Complexity: O(logn)
Auxiliary Space: O(1)
Check if N is a power of K or not:
Given two integers N and K, the task is to check if Y is power of X or not.
Examples:
Input: N = 8, K = 2
Output: Yes
Input: N = 27, K = 3
Output: Yes
Approach: The idea is to take log of N in base K. If it turns out to be an integer, then N is a power of K.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
bool isPower(int N, int K)
{
int res1 = log(N) / log(K);
double res2 = log(N) / log(K);
return (res1 == res2);
}
int main()
{
int N = 8;
int K = 2;
if (isPower(N, K)) {
cout << "Yes";
}
else {
cout << "No";
}
return 0;
}
|
C
#include <stdio.h>
#include <math.h>
_Bool isPower(int N, int K)
{
int res1 = log(N) / log(K);
double res2 = log(N) / log(K);
return (res1 == res2);
}
int main()
{
int N = 8;
int K = 2;
if (isPower(N, K))
{
printf("Yes");
}
else
{
printf("No");
}
return 0;
}
|
Java
class GFG{
static boolean isPower(int N, int K)
{
int res1 = (int)(Math.log(N) / Math.log(K));
double res2 = Math.log(N) / Math.log(K);
return (res1 == res2);
}
public static void main(String[] args)
{
int N = 8;
int K = 2;
if (isPower(N, K))
{
System.out.println("Yes");
}
else
{
System.out.println("No");
}
}
}
|
Python3
from math import log
def isPower(n, k):
res1 = int(log(n) / log(k))
res2 = log(n) / log(k)
return(res1 == res2)
if __name__=="__main__":
n = 8
k = 2
if (isPower(n, k)):
print("Yes")
else:
print("No")
|
C#
using System;
class GFG{
static bool isPower(int N, int K)
{
int res1 = (int)(Math.Log(N) / Math.Log(K));
double res2 = Math.Log(N) / Math.Log(K);
return (res1 == res2);
}
public static void Main()
{
int N = 8;
int K = 2;
if (isPower(N, K))
{
Console.Write("Yes");
}
else
{
Console.Write("No");
}
}
}
|
Javascript
<script>
function isPower(N, K)
{
var res1 = Math.floor(Math.log(N) / Math.log(K));
var res2 = Math.log(N) / Math.log(K);
return (res1 == res2);
}
var N = 8;
var K = 2;
if (isPower(N, K)) {
document.write("Yes");
}
else {
document.write("No");
}
</script>
|
Time Complexity: O(logn)
Auxiliary Space: O(1)
To find the power of K greater than equal to and less than equal to N:
Given two integers N and K, the task is to find the power of K greater than equal to and less than equal to N.
Examples:
Input: N = 7, K = 2
Output: 4 8
Input: N = 18, K = 3
Output: 9 27
Approach: The idea is to find the floor value of the log K value of the given integer N, Then compute the Kth power of this number to compute the previous and next Kth power.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int prevPowerofK(int n, int k)
{
int p = (int)(log(n) / log(k));
return (int)pow(k, p);
}
int nextPowerOfK(int n, int k)
{
return prevPowerofK(n, k) * k;
}
int main()
{
int N = 7;
int K = 2;
cout << prevPowerofK(N, K) << " ";
cout << nextPowerOfK(N, K) << endl;
return 0;
}
|
C
#include <stdio.h>
#include <math.h>
int prevPowerofK(int n, int k)
{
int p = (int)(log(n) / log(k));
return (int)pow(k, p);
}
int nextPowerOfK(int n, int k)
{
return prevPowerofK(n, k) * k;
}
int main()
{
int N = 7;
int K = 2;
printf("%d ", prevPowerofK(N, K));
printf("%d\n", nextPowerOfK(N, K));
return 0;
}
|
Java
class GFG{
static int prevPowerofK(int n, int k)
{
int p = (int)(Math.log(n) / Math.log(k));
return (int)Math.pow(k, p);
}
static int nextPowerOfK(int n, int k)
{
return prevPowerofK(n, k) * k;
}
public static void main(String[] args)
{
int N = 7;
int K = 2;
System.out.print(prevPowerofK(N, K) + " ");
System.out.println(nextPowerOfK(N, K));
}
}
|
Python3
from math import log
def prevPowerofK(n, k):
p = (int)(log(n) / log(k));
return pow(k, p);
def nextPowerOfK(n, k):
return prevPowerofK(n, k) * k;
if __name__=="__main__":
N = 7
K = 2
print(prevPowerofK(N, K), end = " ")
print(nextPowerOfK(N, K))
|
C#
using System;
class GFG{
static int prevPowerofK(int n, int k)
{
int p = (int)(Math.Log(n) / Math.Log(k));
return (int)Math.Pow(k, p);
}
static int nextPowerOfK(int n, int k)
{
return prevPowerofK(n, k) * k;
}
public static void Main()
{
int N = 7;
int K = 2;
Console.Write(prevPowerofK(N, K) + " ");
Console.Write(nextPowerOfK(N, K));
}
}
|
Javascript
<script>
function prevPowerofK(n, k)
{
let p = parseInt(Math.log(n) /
Math.log(k), 10);
return Math.pow(k, p);
}
function nextPowerOfK(n, k)
{
return prevPowerofK(n, k) * k;
}
let N = 7;
let K = 2;
document.write(prevPowerofK(N, K) + " ");
document.write(nextPowerOfK(N, K));
</script>
|
Time Complexity: O(logn)
Auxiliary Space: O(1)
To Find the position of rightmost set bit:
Given an integer N, the task is to find the position of the rightmost set bit.
Examples:
Input: N = 7
Output: 1
Input: N = 8
Output: 4
Approach:
- Take two’s complement of the given no as all bits are reverted except the first ‘1’ from right to left (0111)
- Do a bit-wise & with original no, this will return no with the required one only (0100)
- Take the log2 of the no, you will get (position – 1) (2)
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
unsigned int getFirstSetBitPos(int n)
{
return log2(n & -n) + 1;
}
int main()
{
int N = 8;
cout << getFirstSetBitPos(N);
return 0;
}
|
C
#include <stdio.h>
#include <math.h>
unsigned int getFirstSetBitPos(int n)
{
return log2(n & -n) + 1;
}
int main()
{
int N = 8;
printf("%d", getFirstSetBitPos(N));
return 0;
}
|
Java
class GFG{
static int getFirstSetBitPos(int n)
{
return (int)(Math.log(n & -n) /
Math.log(2)) + 1;
}
public static void main(String[] args)
{
int N = 8;
System.out.println(getFirstSetBitPos(N));
}
}
|
Python3
import math
def getFirstSetBitPos(n):
return math.log2(n & -n) + 1;
if __name__=="__main__":
N = 8
print(int(getFirstSetBitPos(N)))
|
C#
using System;
class GFG{
static int getFirstSetBitPos(int n)
{
return (int)(Math.Log(n & -n) /
Math.Log(2)) + 1;
}
public static void Main()
{
int N = 8;
Console.Write(getFirstSetBitPos(N));
}
}
|
Javascript
<script>
function getFirstSetBitPos(n)
{
return parseInt(Math.log(n & -n) / Math.log(2), 10) + 1;
}
let N = 8;
document.write(getFirstSetBitPos(N));
</script>
|
Time Complexity: O(logn)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...