Lobb Number
Last Updated :
15 May, 2023
In combinatorial mathematics, the Lobb number Lm, n counts the number of ways that n + m open parentheses can be arranged to form the start of a valid sequence of balanced parentheses.
The Lobb number are parameterized by two non-negative integers m and n with n >= m >= 0. It can be obtained by:
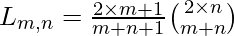
Lobb Number is also used to count the number of ways in which n + m copies of the value +1 and n – m copies of the value -1 may be arranged into a sequence such that all of the partial sums of the sequence are non- negative.
Examples :
Input : n = 3, m = 2
Output : 5
Input : n =5, m =3
Output :35
The idea is simple, we use a function that computes binomial coefficients for given values. Using this function and above formula, we can compute Lobb numbers.
C++
#include <bits/stdc++.h>
#define MAXN 109
using namespace std;
int binomialCoeff(int n, int k)
{
int C[n + 1][k + 1];
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= min(i, k); j++) {
if (j == 0 || j == i)
C[i][j] = 1;
else
C[i][j] = C[i - 1][j - 1] + C[i - 1][j];
}
}
return C[n][k];
}
int lobb(int n, int m)
{
return ((2 * m + 1) * binomialCoeff(2 * n, m + n)) / (m + n + 1);
}
int main()
{
int n = 5, m = 3;
cout << lobb(n, m) << endl;
return 0;
}
|
Java
import java.util.*;
class GFG {
static int binomialCoeff(int n, int k)
{
int C[][] = new int[n + 1][k + 1];
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= Math.min(i, k);
j++) {
if (j == 0 || j == i)
C[i][j] = 1;
else
C[i][j] = C[i - 1][j - 1] +
C[i - 1][j];
}
}
return C[n][k];
}
static int lobb(int n, int m)
{
return ((2 * m + 1) * binomialCoeff(2 * n, m + n)) /
(m + n + 1);
}
public static void main(String[] args)
{
int n = 5, m = 3;
System.out.println(lobb(n, m));
}
}
|
Python 3
def binomialCoeff(n, k):
C = [[0 for j in range(k + 1)]
for i in range(n + 1)]
for i in range(0, n + 1):
for j in range(0, min(i, k) + 1):
if (j == 0 or j == i):
C[i][j] = 1
else:
C[i][j] = (C[i - 1][j - 1]
+ C[i - 1][j])
return C[n][k]
def lobb(n, m):
return (((2 * m + 1) *
binomialCoeff(2 * n, m + n))
/ (m + n + 1))
n = 5
m = 3
print(int(lobb(n, m)))
|
C#
using System;
class GFG {
static int binomialCoeff(int n, int k)
{
int[, ] C = new int[n + 1, k + 1];
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= Math.Min(i, k);
j++) {
if (j == 0 || j == i)
C[i, j] = 1;
else
C[i, j] = C[i - 1, j - 1]
+ C[i - 1, j];
}
}
return C[n, k];
}
static int lobb(int n, int m)
{
return ((2 * m + 1) * binomialCoeff(
2 * n, m + n)) / (m + n + 1);
}
public static void Main()
{
int n = 5, m = 3;
Console.WriteLine(lobb(n, m));
}
}
|
PHP
<?php
$MAXN =109;
function binomialCoeff($n, $k)
{
$C= array(array());
for ($i = 0; $i <= $n; $i++)
{
for ($j = 0; $j <= min($i, $k); $j++)
{
if ($j == 0 || $j == $i)
$C[$i][$j] = 1;
else
$C[$i][$j] = $C[$i - 1][$j - 1] +
$C[$i - 1][$j];
}
}
return $C[$n][$k];
}
function lobb($n, int $m)
{
return ((2 * $m + 1) *
binomialCoeff(2 * $n, $m + $n)) /
($m + $n + 1);
}
$n = 5;$m = 3;
echo lobb($n, $m);
?>
|
Javascript
<script>
function binomialCoeff(n, k)
{
let C = new Array(n + 1);
for (var i = 0; i < C.length; i++) {
C[i] = new Array(2);
}
for (let i = 0; i <= n; i++) {
for (let j = 0; j <= Math.min(i, k);
j++) {
if (j == 0 || j == i)
C[i][j] = 1;
else
C[i][j] = C[i - 1][j - 1] +
C[i - 1][j];
}
}
return C[n][k];
}
function lobb(n, m)
{
return ((2 * m + 1) * binomialCoeff(2 * n, m + n)) /
(m + n + 1);
}
let n = 5, m = 3;
document.write(lobb(n, m));
</script>
|
Time Complexity: O(2*n*(m+n))
Auxiliary Space: O((2*n)*(m+n))
Efficient approach: Space optimization
In previous approach the current value dp[i][j] is only depend upon the current and previous row values of DP. So to optimize the space complexity we use a single 1D array to store the computations.
Implementation steps:
- Create a 1D vector C of size K+1.
- Set a base case by initializing the values of C.
- Now iterate over subproblems by the help of nested loop and get the current value from previous computations.
- At last return and print the final answer stored in C[K].
Implementation:
C++
#include <bits/stdc++.h>
#define MAXN 109
using namespace std;
int binomialCoeff(int n, int k)
{
int C[k+1];
memset(C, 0, sizeof(C));
C[0] = 1;
for (int i = 1; i <= n; i++)
{
for (int j = min(i, k); j > 0; j--)
C[j] = C[j] + C[j-1];
}
return C[k];
}
int lobb(int n, int m)
{
return ((2 * m + 1) * binomialCoeff(2 * n, m + n)) / (m + n + 1);
}
int main()
{
int n = 5, m = 3;
cout << lobb(n, m) << endl;
return 0;
}
|
Java
import java.util.Arrays;
public class LobbNumber {
static int binomialCoeff(int n, int k) {
int[] C = new int[k + 1];
Arrays.fill(C, 0);
C[0] = 1;
for (int i = 1; i <= n; i++) {
for (int j = Math.min(i, k); j > 0; j--) {
C[j] = C[j] + C[j - 1];
}
}
return C[k];
}
static int lobb(int n, int m) {
return ((2 * m + 1) * binomialCoeff(2 * n, m + n)) / (m + n + 1);
}
public static void main(String[] args) {
int n = 5, m = 3;
System.out.println(lobb(n, m));
}
}
|
Python3
def binomialCoeff(n, k):
C = [0] * (k+1)
C[0] = 1
for i in range(1, n+1):
j = min(i, k)
while j > 0:
C[j] = C[j] + C[j-1]
j -= 1
return C[k]
def lobb(n, m):
return ((2 * m + 1) * binomialCoeff(2 * n, m + n)) // (m + n + 1)
if __name__ == "__main__":
n = 5
m = 3
print(lobb(n, m))
|
C#
using System;
public class Program
{
static int binomialCoeff(int n, int k)
{
int[] C = new int[k + 1];
Array.Fill(C, 0);
C[0] = 1;
for (int i = 1; i <= n; i++)
{
for (int j = Math.Min(i, k); j > 0; j--)
C[j] = C[j] + C[j - 1];
}
return C[k];
}
static int lobb(int n, int m)
{
return ((2 * m + 1) * binomialCoeff(2 * n, m + n)) / (m + n + 1);
}
public static void Main()
{
int n = 5, m = 3;
Console.WriteLine(lobb(n, m));
}
}
|
Javascript
function binomialCoeff(n, k) {
let C = new Array(k + 1).fill(0);
C[0] = 1;
for (let i = 1; i <= n; i++) {
for (let j = Math.min(i, k); j > 0; j--)
C[j] = C[j] + C[j - 1];
}
return C[k];
}
function lobb(n, m) {
return ((2 * m + 1) * binomialCoeff(2 * n, m + n)) / (m + n + 1);
}
let n = 5, m = 3;
console.log(lobb(n, m));
|
Time Complexity: O(n^2)
Auxiliary Space: O(k)
Share your thoughts in the comments
Please Login to comment...