Linear Search vs Binary Search

Prerequisite:

• Linear Search
• Binary Search

LINEAR SEARCH

Assume that item is in an array in random order and we have to find an item. Then the only way to search for a target item is, to begin with, the first position and compare it to the target. If the item is at the same, we will return the position of the current item. Otherwise, we will move to the next position. If we arrive at the last position of an array and still can not find the target, we return -1. This is called the Linear search or Sequential search.

Below is the code syntax for the linear search.

C++

// Linear Search in C++

#include <iostream>
using namespace std;

int search(int array[], int n, int x)
{

    // Going through array sequencially
    for (int i = 0; i < n; i++)
        if (array[i] == x)
            return i;
    return -1;
}

C

// Linear Search in C

#include <stdio.h>

int search(int array[], int n, int x)
{

    // Going through array sequencially
    for (int i = 0; i < n; i++)
        if (array[i] == x)
            return i;
    return -1;
}

Java

/*package whatever //do not write package name here */

import java.io.*;

class Main {
    public static int liner(int arr[], int x)
    {
        for (int i = 0; i < arr.length; i++) {
            if (arr[i] == x)
                return i;
        }
        return -1;
    }
}

Python

# Linear Search in Python


def linearSearch(array, n, x):

    for i in range(0, n):
        if (array[i] == x):
            return i
    return -1

C#

// Linear Search in c#
using System;
using System.Collections.Generic;

class GFG
{
  public static int search(int[] array, int n, int x)
  {
    // Going through array sequencially
    for (int i = 0; i < n; i++)
        if (array[i] == x)
            return i;
    return -1;
  }
}

// This code is contributed by adityapatil12.

Javascript

<script>

// Linear Search in C++

function search(array, n, x)
{

    // Going through array sequencially
    for (let i = 0; i < n; i++){
        if (array[i] == x){
            return i;
        }
    }
    return -1;
}

// The coee is contributed by Gautam goel.
</script>

BINARY SEARCH

In a binary search, however, cut down your search to half as soon as you find the middle of a sorted list. The middle element is looked at to check if it is greater than or less than the value to be searched. Accordingly, a search is done to either half of the given list

Below is the code syntax for the binary search.

C++

#include <iostream>
using namespace std;

int binarySearch(int array[], int x, int low, int high)
{

    // Repeat until the pointers low and high meet each
    // other
    while (low <= high) {
        int mid = low + (high - low) / 2;

        if (array[mid] == x)
            return mid;

        if (array[mid] < x)
            low = mid + 1;

        else
            high = mid - 1;
    }

    return -1;
}

C

#include <stdio.h>

int binarySearch(int array[], int x, int low, int high)
{
    // Repeat until the pointers low and high meet each
    // other
    while (low <= high) {
        int mid = low + (high - low) / 2;

        if (array[mid] == x)
            return mid;

        if (array[mid] < x)
            low = mid + 1;

        else
            high = mid - 1;
    }

    return -1;
}

Java

/*package whatever //do not write package name here */

class GFG {
    public static int binary(int[] arr, int x)
    {
        int start = 0;
        int end = arr.length - 1;
        while (start <= end) {
            int mid = (start + end) / 2;
            if (x == arr[mid]) {
                return mid;
            }
            else if (x > arr[mid]) {
                start = mid + 1;
            }
            else {
                end = mid - 1;
            }
        }
        return -1;
    }
}

Python

def binarySearch(array, x, low, high):

    # Repeat until the pointers low and high meet each other
    while low <= high:

        mid = low + (high - low)//2

        if array[mid] == x:
            return mid

        elif array[mid] < x:
            low = mid + 1

        else:
            high = mid - 1

    return -1

C#

// Linear Search in c#
using System;
using System.Collections.Generic;

class GFG
{
  public static int binary(int[] arr, int x)
  {
    int start = 0;
    int end = arr.Length - 1;
    while (start <= end) {
        int mid = (start + end) / 2;
        if (x == arr[mid]) {
            return mid;
        }
        else if (x > arr[mid]) {
            start = mid + 1;
        }
        else {
            end = mid - 1;
        }
    }
    return -1;
  }
}

// This code is contributed by aditya942003patil

Javascript

<script>

function binarySearch(array, x, low, high)
{

    // Repeat until the pointers low and high meet each
    // other
    while (low <= high) {
        int mid = low + (high - low) / 2;

        if (array[mid] == x){
            return mid;
        }

        if (array[mid] < x){
            low = mid + 1;
        }
        else{
            high = mid - 1;
        }

    }

    return -1;
}

// The code is contributed by gautam goel.

</script>

Important Differences

Linear Search	Binary Search
In linear search input data need not to be in sorted.	In binary search input data need to be in sorted order.
It is also called sequential search.	It is also called half-interval search.
The time complexity of linear search O(n).	The time complexity of binary search O(log n).
Multidimensional array can be used.	Only single dimensional array is used.
Linear search performs equality comparisons	Binary search performs ordering comparisons
It is less complex.	It is more complex.
It is very slow process.	It is very fast process.

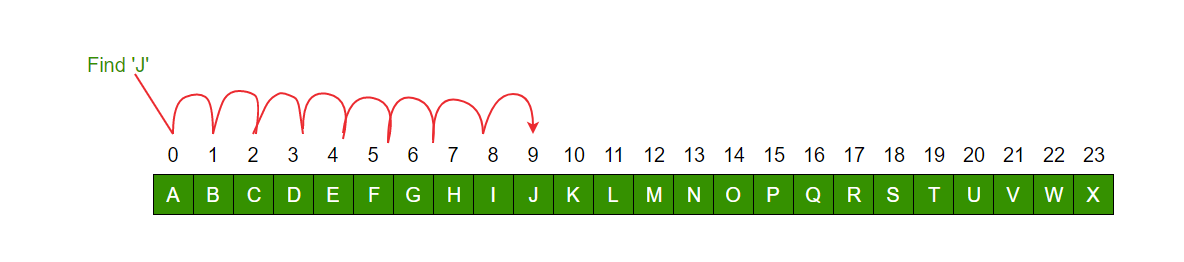
Let us look at an example to compare the two:

Linear Search to find the element “J” in a given sorted list from A-X

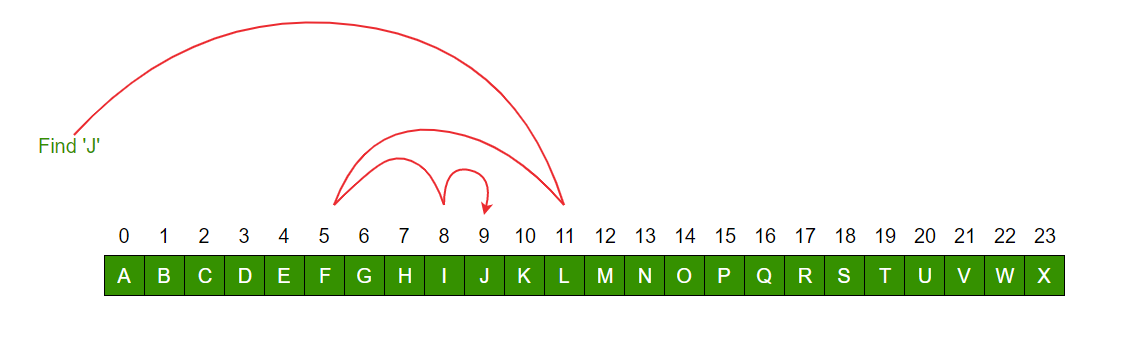
Binary Search to find the element “J” in a given sorted list from A-X

LINER SEARCHING EXAMPLE:

C

#include <stdio.h>

int search(int array[], int n, int x)
{

    // Going through array sequencially
    for (int i = 0; i < n; i++)
        if (array[i] == x)
            return i;
    return -1;
}

int main()
{
    int array[] = { 12, 114, 0, 4, 9 };
    int x = 4;
    int n = sizeof(array) / sizeof(array[0]);

    int result = search(array, n, x);

    (result == -1)
        ? printf("Element not found")
        : printf("Element found at index: %d", result);
}

C++

#include <iostream>
using namespace std;

int search(int array[], int n, int x)
{

    // Going through array sequencially
    for (int i = 0; i < n; i++)
        if (array[i] == x)
            return i;
    return -1;
}

int main()
{
    int array[] = { 12, 114, 0, 4, 9 };
    int x = 4;
    int n = sizeof(array) / sizeof(array[0]);

    int result = search(array, n, x);

    (result == -1)
        ? cout << "Element not found"
        : cout << "Element found at index: " << result;
}

Java

/*package whatever //do not write package name here */
import java.io.*;

class GFG {
    public static int liner(int arr[], int x)
    {
        for (int i = 0; i < arr.length; i++) {
            if (arr[i] == x)
                return i;
        }
        return -1;
    }
    public static void main(String[] args)
    {
          int arr[] = { 12, 114, 0, 4, 9 };

        int search = liner(
            arr,
            4); // Here we are searching for 10 element in
                 // the array which is not present in the
                 // array so, it will print -1
        System.out.println(search);
    }
}

Python

def linearSearch(array, n, x):

    for i in range(0, n):
        if (array[i] == x):
            return i
    return -1


array = [24, 41, 31, 11, 9]
x = 11
n = len(array)
result = linearSearch(array, n, x)
if(result == -1):
    print("Element not found")
else:
    print("Element is Present at Index: ", result)

C#

// C# program to implement above approach
using System;
using System.Collections.Generic;

class GFG
{
  public static int liner(int[] arr, int x)
  {
    for (int i = 0; i < arr.Length; i++) {
        if (arr[i] == x)
            return i;
    }
    return -1;
  }

  // Driver Code
  public static void Main(string[] args){

    int[] arr = { 12, 114, 0, 4, 9 };
    int search = liner(arr, 4); // Here we are searching for 10 element in
                                 // the array which is not present in the
                                 // array so, it will print -1
    Console.Write(search);
  }
}
//this code is contributed by aditya942003patil

Javascript

function search(array, n, x)
{

    // Going through array sequencially
    for (let i = 0; i < n; i++)
        if (array[i] == x)
            return i;
    return -1;
}


array = [12, 114, 0, 4, 9 ];
x = 4;
n = array.length;
result = search(array, n, x);


if(result == -1){
    console.log("Element not found");
}
else{
    console.log("Elementn found at index: ", result);
}

// The code is contributed by Nidhi goel

Output

Element found at index: 3

Complexity Analysis:

Time Complexity: O(n) – where n is the size of the input array. The worst-case scenario is when the target element is not present in the array, and the function has to go through the entire array to figure that out.

Auxiliary Space: O(1) – the function uses only a constant amount of extra space to store variables. The amount of extra space used does not depend on the size of the input array.

BINARY SEARCHING EXAMPLE:

C

#include <stdio.h>

int binarySearch(int array[], int x, int low, int high)
{
    // Repeat until the pointers low and high meet each
    // other
    while (low <= high) {
        int mid = low + (high - low) / 2;

        if (array[mid] == x)
            return mid;

        if (array[mid] < x)
            low = mid + 1;

        else
            high = mid - 1;
    }

    return -1;
}

int main( )
{
    int array[] = { 2, 4, 5, 17, 14, 7, 11, 22 };
    int n = sizeof(array) / sizeof(array[0]);
    int x = 22;
    int result = binarySearch(array, x, 0, n - 1);
    if (result == -1)
        printf("Not found");
    else
        printf(" %d", result);
    return 0;
}

C++

#include<bits/stdc++.h>
using namespace std;

int binarySearch(vector<int> arr,int x,int low,int high){

    while(low <= high){

        int mid = low + (high - low)/2;

        if (arr[mid] == x)
            return mid;

        else if (arr[mid] < x)
            low = mid + 1;
        else
            high = mid - 1;
    }

    return -1;
}

int main(){
    vector<int> arr = {2, 4, 5, 17, 14, 7, 11, 22};
    int x = 22;

    int result = binarySearch(arr, x, 0, arr.size()-1);

    if (result != -1)
        cout << result << endl;
    else
        cout << "Not found" << endl;
    return 0;
}


// The code is constributed by Nidhi goel

Java

/*package whatever //do not write package name here */

public class GFG {
    public static int binary(int arr[], int x)
    {
        int start = 0;
        int end = arr.length - 1;
        while (start <= end) {
            int mid = (start + end) / 2;
            if (x == arr[mid]) {
                return mid;
            }
            else if (x > arr[mid]) {
                start = mid + 1;
            }
            else {
                end = mid - 1;
            }
        }
        return -1;
    }
    public static void main(String[] args)
    {
        int arr[] = { 2, 4, 5, 17, 14, 7, 11, 22 };
        int search = binary(arr, 22);
        System.out.println(search);
    }
}

Python

def binarySearch(array, x, low, high):

    while low <= high:

        mid = low + (high - low)//2

        if array[mid] == x:
            return mid

        elif array[mid] < x:
            low = mid + 1

        else:
            high = mid - 1

    return -1


array = [2, 4, 5, 17, 14, 7, 11, 22]
x = 22

result = binarySearch(array, x, 0, len(array)-1)

if result != -1:
    print(str(result))
else:
    print("Not found")

C#

using System;
using System.Collections.Generic;

class GFG
{
  public static int binary(int[] arr, int x)
  {
    int start = 0;
    int end = arr.Length - 1;
    while (start <= end) {
        int mid = (start + end) / 2;
        if (x == arr[mid]) {
            return mid;
        }
        else if (x > arr[mid]) {
            start = mid + 1;
        }
        else {
            end = mid - 1;
        }
    }
    return -1;
  }

  // Driver Code
  public static void Main(string[] args){

    int[] arr = { 2, 4, 5, 17, 14, 7, 11, 22 };
    int search = binary(arr, 22);
    Console.Write(search);
  }
}
// This code is contributed by aditya942003patil

Javascript

<script>

function binarySearch(array, x, low, high){

    while(low <= high){

        let mid = low + Math.floor((high - low)/2);

        if (array[mid] == x)
            return mid;

        else if (array[mid] < x)
            low = mid + 1;
        else
            high = mid - 1;
    }

    return -1;
}

let array = [2, 4, 5, 17, 14, 7, 11, 22];
let x = 22;

let result = binarySearch(array, x, 0, array.length-1);
if (result != -1)
    console.log(result);
else
    console.log("Not found");

// The code is constributed by Nidhi goel
</script>

Output

 7

Complexity Analysis:

Time Complexity: O(log n) – Binary search algorithm divides the input array in half at every step, reducing the search space by half, and hence has a time complexity of logarithmic order.

Auxiliary Space: O(1) – Binary search algorithm requires only constant space for storing the low, high, and mid indices, and does not require any additional data structures, so its auxiliary space complexity is O(1).