A Linear equation is defined as an equation with the maximum degree of one only, for example, ax = b can be referred to as a linear equation, and when a Linear equation in two variable comes into the picture, it means that the entire equation has 2 variables present in it. Therefore, Linear Equation in two variables can be written in the general form of, ax + by + c = 0, where a, b, c are the constants and x, y are the variables.
Linear Equation in Two Variables
A linear equation in two variables is given by,
Ax + By + C = 0
Where, A, B, and C are constant real numbers, and A and B both are never zero.
Let’s see how to formulate such an equation through a real-life example.
Question: A one-day international match was played between Australia and India in Nagpur. Two Indian batsmen scored a total of 176 runs. Express this information in the form of an equation.
Answer:
We know that two batsmen scored 176 runs, but we do not know how much each batsman scored. Let the runs scored by each batsman be “x” and “y”.
So, x + y = 176.
This is the required linear equation in two variables.
Linear equations in one variable can also be represented as a linear equation in two variables. For example: x = 3, it can also be re-written as
x.1 + y.0 = 3
Solutions of Linear Equation in two Variables
We have seen equations such as x = 5, y = 10. They have only one solution. But when it comes to linear equations in two variables. There are more than one solution,
For example: Let’s assume an equation in two variables,
x + 2y = 4
To find the solutions to this equation, we need to know the values of x and y which satisfy this equation. Here x = 2 and y = 1 is a solution, let’s verify it. Plug in the values of x and y in the equation given above.
x + 2y = 4
⇒ (2) + 2(1) = 4
⇒ 2 + 2 = 4
Hence, x = 2 and y = 1 is a solution this equation. Similarly, we can also verify that x = 2 and y = 1 is also a solution. We can do more solution like this by simply assuming a value of x and then putting in the equation. For example: let’s assume x = 4. Now plug it in the equation, the equation reduces to a single variable equation.
4 + 2y = 4
⇒2y = 0
⇒y = 0
So, if we keep on taking different values of x, we can find infinitely many solutions to these equations.
Thus, we can say, Linear Equations in two variables have infinitely many solutions.
Question 1: Find three different solutions to the equation y + 5x = 10.
Solution:
To find different solutions, we simply have to assume a value of x or y. Plug it in the equation and reduce it in a single variable equation. This way we can find the value of other variable.
Let’s say x = 2. Plug it in the equation,
y + 5(2) = 10
⇒y + 10 = 10
⇒y = 0
So, (2,0) is a solution.
Now let’s say x = 3 and plug it in the equation,
y + 5(3) = 10
⇒ y + 15 = 10
⇒ y = 10 – 15
⇒ y = -5
The solution comes out to be (3, -5)
For the last required solution assume x = 0 and plug it in,
y + 5(0) = 10
⇒ y = 10
The solution comes out to be (2,10)
Thus, the three solutions are :- (2,0); (3,-5) and (2,10).
Graph of Linear Equation in Two Variables
So far we have seen solutions of linear equations. There are infinitely many solutions to a linear equation in two variables. Let’s look at their geometric interpretation. We can show all the solutions in a coordinate plane and see what it looks like. Let’s see how to do this.
Let’s take an example, x + 2y = 6.
Its solutions can be arranged in the form of the table given below.
Let’s plot (0,3); (2,2); (4,1) and (6,0) on the graph.
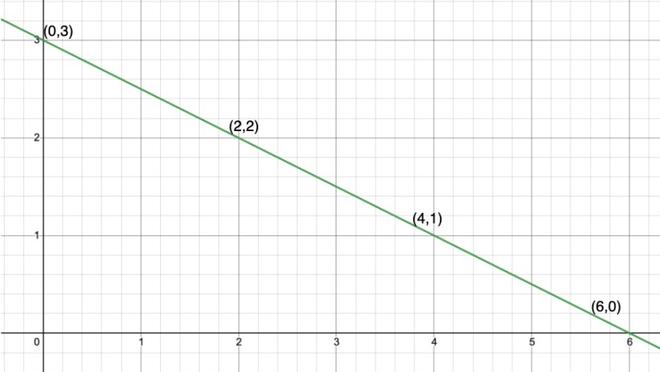
Notice that all these points when joined form a straight line. Every point on this line satisfies the equation and every solution of this equation is on the line. This is called a graph of the linear equation. To plot the graph of a linear equation we require a minimum of two solutions of the equation.
Graphing Linear Equation by Plotting Points:
- Find three points whose coordinates are solutions to the equation.
- Plot the points in a graph.
- Draw a line through all three points.
Let’s take an example,
Question: Plot the equation of line 2x + y = 4 using the method mentioned above.
Solution:
First let’s find three points which satisfy this equation. This is done by the method previously discussed
Let’s put x = 0, then y comes out to be y = 4. So (0,4) is one point.
Putting y = 0, we get, x = 2. So (2,0) is another point.
Putting x = 1, we get y = 2. So (1,2) is the third point.
Let’s plot the points given in the table and join them to form a line.
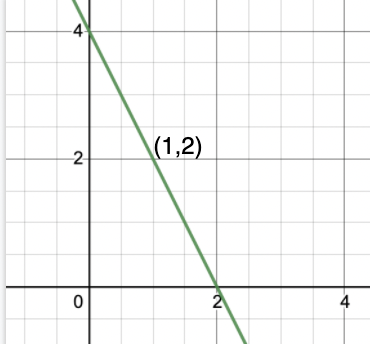
The figure represents our required line.
Equation of lines parallel to x-axis and y-axis
Let’s consider the equation x = 3.
Now when this equation is treated as a single variable equation, it has only solution x = 3. But when we treat it as an equation in two variables
x + 0.y = 3. This equation has infinitely many solutions. Let’s plot graphs of such equations.
Question 1: Plot the equation of x = 4.
Solution:
Let’s find the solution for this equation
x + 0.y = 4
x = 4 satisfies the equation, and we can put any value in place of y, it won’t affect the solution. Thus, the solutions to this equation look like this,
Let’s plot this points on graph and get the line.

Question 2: Plot the graph of y = 3.
Solution:
Let’s find the solution for this equation
0.x + y = 3
y = 3 satisfies the equation, and we can put any value in place of y, it won’t affect the solution. Thus, the solutions to this equation look like this,
Let’s plot this points on graph and get the line.

Question 3: A taxi fare in Bangalore is as follows: For the first kilometer it is Rs.10 and then the subsequent distance is measured in Rs.5 per kilometer. Formulate the linear equation for this problem and draw its graph.
Solution:
Let the total distance traveled by “x” Km and the total fare be “y”.
y = 10 + (x – 1)5
⇒ y= 10 + 5x -5
⇒ y = 5x + 5
Now let’s find the solutions to this equation and plot it.
The table represents three solutions of the equation. Let’s plot these points on the graph and join them to make a straight line.

Question 4: Rahul and Ravi contributed a total of Rs 100 towards the Covid Relief Fund set up by the government. Formulate the equation which satisfies the data and plot its graph.
Answer:
Let the contribution of Rahul be Rs. x and that of Ravi be Rs. y.
Then equation can be formed as,
x + y = 100
Again, let’s find some solutions to this equation.
Plotting the points on the graph.

Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...