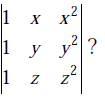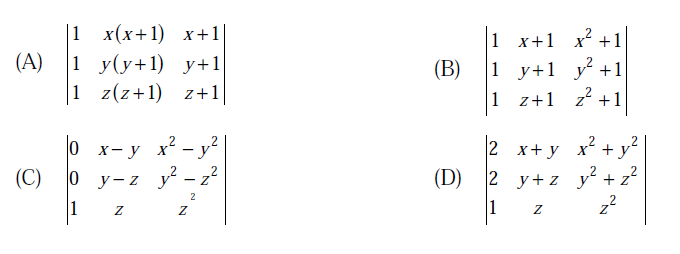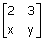Linear Algebra

Question 1

Which one of the following does NOT equal to 

• C
  

• D
  

• B
  

• A
  

Question 2

Let A be the 2 × 2 matrix with elements a11 = a12 = a21 = +1 and a22 = −1. Then the eigenvalues of the matrix A¹⁹ are

• A
• B
• C
• D

Question 3

Consider the matrix as given below.

Which one of the following options provides the CORRECT values of the eigenvalues of the matrix?

• 1, 4, 3
• 3, 7, 3
• 7, 3, 2
• 1, 2, 3

Question 4

Consider the following matrix 
A = 

If the eigenvalues of A are 4 and 8, then 

• x=-3, y=9
  

• x= -4, y=10
  

• x=5, y=8
  

• x=4, y=10
  

Question 5

Consider a matrix [Tex]A = uv^T[/Tex] where [Tex]u = \\begin{pmatrix} 1\\\\ 2 \\end{pmatrix}, v = \\begin{pmatrix} 1\\\\ 1 \\end{pmatrix}[/Tex]. Note that [Tex]v^T[/Tex] denotes the transpose of v. The largest eigenvalue of A is ________ . Note -This was Numerical Type question.

• 0
• 1
• 2
• 3

Question 6

How many of the following matrices have an eigenvalue 1?

• four
  

• three
  

• two
  

• one
  

Question 7

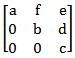
If the matrix A is such that 

[caption width="800"] [/caption]

 then the determinant of A is equal to

• 0

• 1

• 2

• 3

Question 8

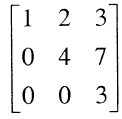
The product of the non-zero eigenvalues of the matrix

1 0 0 0 1
0 1 1 1 0
0 1 1 1 0
0 1 1 1 0
1 0 0 0 1

is ______

• 4

• 5

• 6

• 7

Question 9

Which one of the following statements is TRUE about every 

• If the product of the trace and determinant of the matrix is positive, all its eigenvalues are positive.
  

• If the trace of the matrix is positive, all its eigenvalues are positive. 
  
  

• If the determinant of the matrix is positive, all its eigenvalues are positive.
  

• If the trace of the matrix is positive and the determinant of the matrix is negative, at least one of its eigenvalues is negative.
  

Question 10

Consider the set H of all 3 × 3 matrices of the type 

where a, b, c, d, e and f are real numbers and abc ≠ 0. Under the matrix multiplication operation, the set H is 

• a group
  

• a monoid but not a group
  

• a semigroup but not a monoid
  

• neither a group nor a semigroup