Like and Unlike Terms are the types of terms in algebra, and we can differentiate between like and unlike terms by simply checking the variables and their powers. We define algebraic terms as the individual terms obtained from the algebraic equation.
For example in the algebraic equation 5x + 3y2 = 12 we have three terms that are, 5x, 3y², and 12. Here, 5x, and 3y2 are variable terms and 12 is the constant term. The below image shows the like and unlike terms.
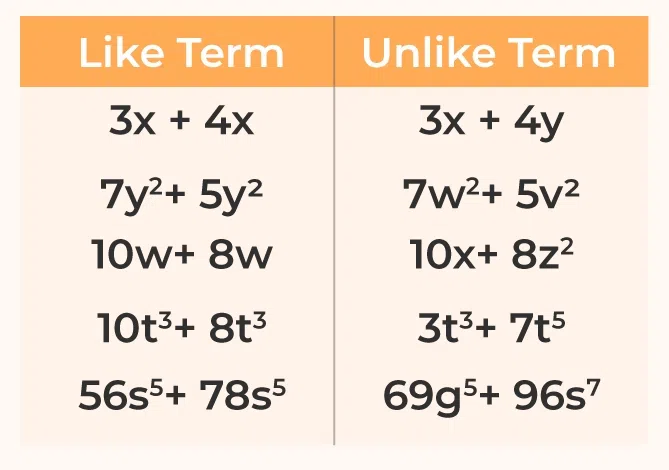
In this article, we will learn about Like Terms, Unlike Terms, their Examples, Simplification, and others in detail.
What are Like Terms?
Like terms are the terms that have the same variables and the power of each of the variables is also the same. We can combine like terms to simplify the algebraic expressions, and this can be calculated very easily. For example, 3y + 5y is an algebraic expression with like terms 3y and 5y. In order to simplify this algebraic expression, we add the like terms. Thus, the simplification of the given expression is 8y.
Examples of Like Terms
Like terms, are the terms that have the same variable with similar power. Some examples of the like terms are,
- 40xy2 and 56xy2: In the first example xy2 is the common coefficient for both terms. So, they are like terms.
- 30z2 and 18z2: z2 is the common coefficient for both terms. So, they are like terms.
- 45abc and 29abc: abc is the common coefficient for both terms. So, they are like terms.
- 18r3 and 38r3: r3 is the common coefficient for both terms. So, they are like terms.
- 2xy and 8xy: xy is the common coefficient for both terms. So, they are like terms.
Addition and Subtraction of Like Terms
We can easily perform addition and subtraction of like terms and it do not require any special rule they are generally simplified using the normal addition and subtraction rules. We can understand this concept using the following example.
Example: Simplify 11x3 + 5x3
Solution:
As we see that these are like term because they have similar variables and their power is also constant.
We can easily add these terms directly.
= 11x3 + 5x3
= 16x3
This is possible because they have the same variables with similar power and this can be understood as, we can directly add rupees to rupees, i.e. 5 Rs + 7 Rs is 12 Rs. But we can not directly add rupees with dollars and 5 Rs + 7 Dollars can not be directly simplified.
Similarly, we can also subtract like terms directly just add we add like terms this can be understood by the following example.
Example 1: Simplify 11x3 – 5x3
Solution:
As we see that these are like term because they have similar variables and their power is also constant.
We can easily subtract these terms directly.
= 11x3 – 5x3
= 6x3
Example 2: Add 3x + 2y + 5 and 4x − 3y + 7.
Solution:
(3x + 2y + 5) + (4x − 3y + 7)
= (3x + 4x) +(2y + (-3y))+ (5 + 7)
= 7x − y + 12
What are Unlike Terms?
Unlike Terms are terms with different variables and each of the variables may or may not have different exponents on them. For example, 9x + 6y is an algebraic expression with, unlike terms. Because it has two different variables x and y. If the variables are different we do not check the power as they are in any way unlike terms but if the variables are the same we check for their powers because they may or may not be like terms.
Such as 5x2 and 6x2 are like terms but, 5x2 and 6x3 are unlike terms.
Examples of Unlike Terms
Unlike terms, are the terms that do neither have the same variables nor similar power. Some examples of unlike terms are,
- 40xy2 and 56xy: Here, in one algebraic expression the variable is xy2 and in the other algebraic expression the variable is xy. Both variables are the same but have different powers. So, they are unlike terms.
- 45abc and 29ab: Here, in one algebraic expression the variable is abc and in the other algebraic expression the variable is ab. Both variables are different. So, they fall into the category of, unlike terms.
Addition and Subtraction of Unlike Terms
Addition and subtraction are not performed between, unlike terms, i.e. we can not add or subtract unlike terms and this can be understood by the example as we can not add 5 liters of milk with 6 kg of rice. In the same way, we can not add or subtract, unlike terms.
For example, 3xy + 5x can not be further solved and it is left in the same way.
Difference Between Like Terms and Unlike Terms
The differences between the like terms and, unlike terms are discussed in the table below,
|
Feature
|
Like Terms
|
Unlike Terms
|
|
Definition
|
Like terms are the terms that have the same variables
and the same exponent values. |
Unlike terms are terms that have different variables
and exponents. |
|
Simplification
|
We can easily simplify the like terms. |
Unlike terms that can not be simplified. |
|
Combining terms
|
Like terms can be combined directly to make calculation.
|
Unlike terms cannot be combined directly because they represent different quantities
|
|
Addition or Subtraction
|
Addition and subtraction can be achieved in Like terms. |
We cannot add or subtract, unlike terms. |
|
Examples
|
Examples of Like terms are, x2, 5x2, -11/3x2, etc. |
Examples of Unlike terms are, x2y, 5x3, -11/3x, etc. |
Related Article,
Examples for Like and Unlike Algebraic Terms
Example 1: Identify like and unlike terms from: 3x, 5xy, 18x2y, 5x3, 29xy, 50x3
Solution:
Like and Unlike terms from the given terms are,
Like Terms: (5xy, 29xy), and (5x3, 50x3)
Unlike Terms: 3x, 18x2y
Example 2: Simplify 3xy + 5x2 + 11ab – 4xy
Solution:
Given Expression:3xy + 5x2 + 11ab – 4xy
Like term in the given expression, 3xy and -4xy
On simplifying,
= 3xy – 4xy + 5x2 + 11ab
= -xy + 5x2 + 11ab
Rest all the terms are unlike terms so they can not be further solved.
Example 3: Simplify 8x + 15x2 + 11x – 4x2
Solution:
Given Expression: 8x + 15x2 + 11x – 4x2
Like term in the given expression, (8x, 11x) and (15x2, -4x2)
On simplifying,
= 8x + 11x + 15x2– 4x2
= 19x – 11x2
Rest all the terms are unlike terms so they can not be further solved.
FAQs on Like and Unlike Algebraic Terms
What are algebraic terms?
Algebraic terms are the individual terms obtained from the algebraic equation i.e., terms divided by the operation symbols such as + and -.
What are Like and Unlike Terms?
Like and unlike terms are the terms of the algebraic expression. In like we have similar variables and the power of the exponent is the same while in unlike terms the variables and their power is different.
What is the Difference Between Like and Unlike Algebraic Terms?
The basic difference between like and unlike terms is that in the like term, we have the same variable with the same powers whereas in, unlike terms we have different variables with different powers.
How to find Like and Unlike Algebraic Terms?
The like terms are the terms that have the same variables with the same powers and the unlike terms are the terms with different variables and different powers and we can easily identify them just by inspecting the variables.
Can we Add or Subtract Like Algebraic Terms?
We can easily add or subtract like terms such as 5x and 11x are like terms and they can be added as 16x.
Can we Add or Subtract Unlike Algebraic Terms?
We can not add or subtract unlike terms such as 2x and 3y. Thus, unlike terms cannot be added or subtracted together.
Share your thoughts in the comments
Please Login to comment...