Lexicographically Smallest Topological Ordering

Given a directed graph with N vertices and M edges that may contain cycles, the task is to find the lexicographically smallest topological ordering of the graph if it exists otherwise print -1 (if the graph has cycles). 
Lexicographically smallest topological ordering means that if two vertices in a graph do not have any incoming edge then the vertex with the smaller number should appear first in the ordering. 
For Example, in the image below many topological orderings are possible e.g 5 2 3 4 0 1, 5 0 2 4 3 1. 
But the smallest ordering is 4 5 0 2 3 1.

Examples:

Input:

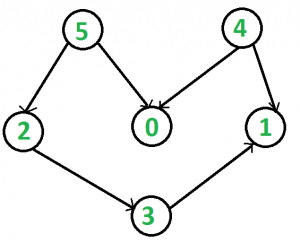
Output: 4 5 0 2 3 1 
Even though 5 4 0 2 3 1 is also a valid topological 
ordering of the given graph but it is not 
lexicographically smallest. 

Approach: We will use Kahn’s algorithm for Topological Sorting with a modification. Instead of using a queue we will use a priority queue to store the vertices to make sure that every time we pick a vertex it is the smallest possible of all. The overall Time complexity changes to [Tex]O(VlogV+E)               [/Tex]
Below is the implementation of the above approach:

CPP

// C++ implementation of the approach #include <bits/stdc++.h> using namespace std; vector<vector<int> > adj; // function to add edge to the graph void addEdge(int x, int y) { adj[x].push_back(y); } // Function to print the required topological // sort of the given graph void topologicalSort() { int V = adj.size(); // Create a vector to store indegrees of all // the vertices // Initialize all indegrees to 0 vector<int> in_degree(V, 0); // Traverse adjacency lists to fill indegrees of // vertices // This step takes O(V+E) time for (int u = 0; u < V; u++) { for (auto x : adj[u]) in_degree[x]++; } // Create a min-heap priority queue and inserting all // vertices with indegree 0 priority_queue<int, vector<int>, greater<int> > pq; for (int i = 0; i < V; i++) if (in_degree[i] == 0) pq.push(i); // Initialize count of visited vertices int cnt = 0; // Create a vector to store result (A topological // ordering of the vertices) vector<int> top_order; // One by one erase vertices from setand insert // adjacents if indegree of adjacent becomes 0 while (!pq.empty()) { // Extract vertex with minimum number from priority // queue and add it to topological order int u = pq.top(); pq.pop(); top_order.push_back(u); // Iterate through all its neighbouring nodes // of erased node u and decrease their in-degree // by 1 for (auto x : adj[u]) // If in-degree becomes zero, add it to queue if (--in_degree[x] == 0) pq.push(x); cnt++; } // Check if there was a cycle if (cnt != V) { cout << -1; return; } // Print topological order for (int i = 0; i < top_order.size(); i++) cout << top_order[i] << " "; } int main() { // number of vertices int v = 6; // adjacency matrix adj = vector<vector<int> >(v); addEdge(5, 2); addEdge(5, 0); addEdge(4, 0); addEdge(4, 1); addEdge(2, 3); addEdge(3, 1); // find required topological order topologicalSort(); }

Java

// Java implementation of the approach import java.util.*; class Main { static List<List<Integer>> adj; // function to add edge to the graph static void addEdge(int x,int y) { adj.get(x).add(y); } // Function to print the required topological // sort of the given graph static void topologicalSort() { int V = adj.size(); // Create a vector to store indegrees of all // the vertices // Initialize all indegrees to 0 int[] in_degree = new int[V]; Arrays.fill(in_degree, 0); // Traverse adjacency lists to fill indegrees of // vertices // This step takes O(V+E) time for (int u = 0; u < V; u++) { for (int x: adj.get(u)) in_degree[x]++; } // Create a queue and inserting all vertices with // indegree 0 PriorityQueue<Integer> queue = new PriorityQueue<>(); for (int i = 0; i < V; i++) if (in_degree[i] == 0) queue.add(i); // Initialize count of visited vertices int cnt = 0; // Create a vector to store result (A topological // ordering of the vertices) List<Integer> top_order = new ArrayList<>(); // One by one erase vertices from queue and insert // adjacents if indegree of adjacent becomes 0 while (!queue.isEmpty()) { // Extract vertex with minimum number from queue // and add it to topological order int u = queue.poll(); top_order.add(u); // Iterate through all its neighbouring nodes // of erased node u and decrease their in-degree // by 1 for (int x: adj.get(u)) // If in-degree becomes zero, add it to queue if (--in_degree[x] == 0) queue.add(x); cnt++; } // Check if there was a cycle if (cnt != V) { System.out.println(-1); return; } // Print topological order for (int i = 0; i < top_order.size(); i++) System.out.print(top_order.get(i) + " "); } public static void main (String[] args) { // number of vertices int v = 6; // adjacency matrix adj = new ArrayList<>(v); for (int i = 0; i < v; i++) { adj.add(new ArrayList<>()); } addEdge(5,2); addEdge(5,0); addEdge(4,0); addEdge(4,1); addEdge(2,3); addEdge(3,1); // find required topological order topologicalSort(); } } // This code is contributed by lokeshpotta20.

Python3

# Python3 implementation of the approach import heapq as hq # function to add edge to the graph def addEdge(x, y): adj[x].append(y) # Function to print required topological # sort of the given graph def topologicalSort(): V = len(adj) # Create a vector to store indegrees of all # the vertices # Initialize all indegrees to 0 in_degree = [0] * V # Traverse adjacency lists to fill indegrees of # vertices # This step takes O(V+E) time for u in range(V): for x in adj[u]: in_degree[x] += 1 # Create a heap and inserting all vertices with # indegree 0 s = [] for i in range(V): if in_degree[i] == 0: hq.heappush(s, i) # Initialize count of visited vertices cnt = 0 # Create a vector to store result (A topological # ordering of the vertices) top_order = [] # One by one erase vertices from setand insert # adjacents if indegree of adjacent becomes 0 while s: # Extract vertex with minimum number from multiset # and add it to topological order u = hq.heappop(s) top_order.append(u) # Iterate through all its neighbouring nodes # of erased node u and decrease their in-degree # by 1 for x in adj[u]: in_degree[x] -= 1 # If in-degree becomes zero, add it to queue if in_degree[x] == 0: hq.heappush(s, x) cnt += 1 # Check if there was a cycle if cnt != V: print(-1) return # Print topological order for i in range(len(top_order)): print(top_order[i], end=" ") if __name__ == "__main__": # number of vertices v = 6 # adjacency matrix adj = [[] for _ in range(v)] addEdge(5, 2) addEdge(5, 0) addEdge(4, 0) addEdge(4, 1) addEdge(2, 3) addEdge(3, 1) # find required topological order topologicalSort()

JavaScript

class PriorityQueue { constructor() { this.queue = []; } add(element) { this.queue.push(element); this.queue.sort((a, b) => a - b); } poll() { return this.queue.shift(); } isEmpty() { return this.queue.length === 0; } } class Main { constructor() { this.adj = []; } // function to add edge to the graph addEdge(x, y) { this.adj[x].push(y); } // Function to print the required topological // sort of the given graph topologicalSort() { const V = this.adj.length; // Create an array to store indegrees of all // the vertices // Initialize all indegrees to 0 const in_degree = new Array(V).fill(0); // Traverse adjacency lists to fill indegrees of // vertices // This step takes O(V+E) time for (let u = 0; u < V; u++) { for (let x of this.adj[u]) in_degree[x]++; } // Create a priority queue and inserting all vertices with // indegree 0 const queue = new PriorityQueue(); for (let i = 0; i < V; i++) if (in_degree[i] == 0) queue.add(i); // Initialize count of visited vertices let cnt = 0; // Create an array to store result (A topological // ordering of the vertices) const top_order = []; // One by one erase vertices from queue and insert // adjacents if indegree of adjacent becomes 0 while (!queue.isEmpty()) { // Extract vertex with minimum number from queue // and add it to topological order let u = queue.poll(); top_order.push(u); // Iterate through all its neighbouring nodes // of erased node u and decrease their in-degree // by 1 for (let x of this.adj[u]) // If in-degree becomes zero, add it to queue if (--in_degree[x] == 0) queue.add(x); cnt++; } // Check if there was a cycle if (cnt != V) { console.log(-1); return; } // Print topological order console.log(top_order.join(" ")); } } // Main function (function () { // number of vertices const v = 6; const main = new Main(); // adjacency matrix for (let i = 0; i < v; i++) { main.adj.push([]); } main.addEdge(5, 2); main.addEdge(5, 0); main.addEdge(4, 0); main.addEdge(4, 1); main.addEdge(2, 3); main.addEdge(3, 1); // find required topological order main.topologicalSort(); })();

Output

4 5 0 2 3 1

Time Complexity: O(N)
Auxiliary Space: O(N)